Экологическое прогнозирование и монито­ринг

Классификация моделей

Математические модели в экологии

Основные вопросы, рассматриваемые на лекции:

1. Классификация моделей.

2. Экологическое прогнозирование и мониторинг.

При экологическом исследовании, которое обычно проводится на определенном количест­ве особей, изучаются природные явления во всем их многообразии: общие закономерности, присущие макросистеме, ее реакции на изме­нения условий существования и др. Но каждая особь, индивидуум неодинаковы, отличны друг от друга. Кроме того, выбор особи из всей популяции носит случайный характер. И лишь применение методов математической статисти­ки дает возможность по случайному набору различных вариантов определить достоверность тех или иных результатов (степень отклонения их от нормы, случайны отклонения или законо­мерны) и получить объективное представление обо всей популяции. Однако, все биологические системы, обладают спо­собностью к саморегуляции и ограничиваться только методами математической статистики стало не­возможно. Поэтому в современной экологии широко применяются методы теории информации и кибернетики, тесно связанные с такими областями математики, как теория вероятности, математическая логика, дифференциальные и интегральные исчисления, теория чисел, матрич­ная алгебра. В последнее время широкое распростране­ние получило моделирование биологических яв­лений, т. е. воспроизведение в искусственных системах различных процессов, свойственных живой природе. Так, в «модельных условиях» были осуществлены многие реакции, протека­ющие в растении при фотосинтезе. Примером биологических моделей может служить и аппа­рат искусственного кровообращения, искусст­венная почка, искусственные легкие, протезы, управляемые биотоками мышц, и др. В различных областях биологии широко при­меняются так называемые живые модели. Не­смотря на то, что различные организмы отлича­ются друг от друга сложностью структуры и функции, многие биологические процессы у них протекают практически одинаково. Поэтому изучать их удобно на более простых существах. Они то и становятся живыми моделями. В каче­стве примера можно привести зоохлореллу, которая служит моделью для изучения обмена веществ; моделью для исследования внутрикле­точных процессов являются гигантские расти­тельные и животные клетки и т. д. Основной задачей биологического модели­рования является экспериментальная проверка гипотез относительно структуры и функции био­логических систем. Сущность этого метода за­ключается в том, что вместе с оригиналом, т. е. с какой-то реальной системой, изучается его искусственно созданное подобие — модель. В сравнении с оригиналом модель обычно уп­рощена, но свойства их сходны. В противном случае полученные результаты могут оказаться недостоверными, не свойственными оригиналу. Т. Г. Гильманов (1980) указывает: «Одно из достоинств метода моделирования состоит в возможности построения моделей с «удобной реализацией», ибо удачный выбор реализации делает исследование модели несравненно бо­лее легким, чем исследование оригинала, и в то же время позволяет сохранить существенные черты его состава, структуры и функционирования». В зависимости от особенностей оригинала и задач исследования применяются самые разнообразные модели (рисунок 1).

Реальные (натурные, аналоговые) моде­ли, если таковые удается создать, отражают самые существенные черты оригинала. Напри­мер, аквариум может служить моделью есте­ственного водоема. Однако создание реальных моделей сопряжено с большими техническими трудностями, так как пока еще не удается до­стичь точного воспроизведения оригинала. Знаковая модель представляет собой условное отображение оригинала с помощью математических выражений или подробного описания. Наибольшее распространение в современ­ных экологических исследованиях получили концептуальные и математические модели и их многочисленные разновидности. Разновидности концептуальных моделей характеризуются подробным описанием системы (научный текст, схема системы, таблицы, графики и т.д.). Математические модели являются более эффективным методом изучения экологических систем, особенно при определении количественных показателей. Математические символы, например, позволяют сжато описать сложные экологические системы, а уравнения дают возможность формально определить взаимодействия различных их компонентов.

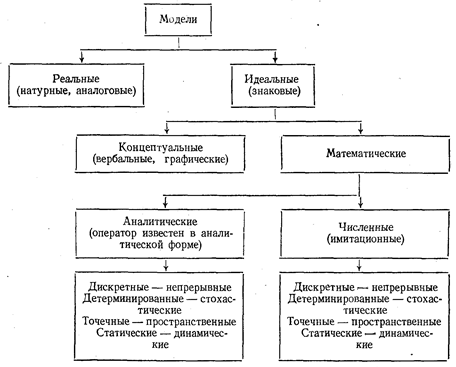
Рисунок 1- Классификация моделей (по В. Д. Федорову и Т. Г. Гильманову, 1980)

Процесс перевода физических или биологи­ческих представлений о любой экологической системе в ряд математических зависимостей и операции над ними называются системным анализом, а сама математическая система — моделью. Следует отметить, что математические модели являются неполным абстрактным отображением реального мира.

По типу реализации различаются реальные и знаковые моде­ли. Реальная модель отражает существенные черты оригинала уже по самой природе своей физической реализации. Например, аквариум с его растительностью, животным и микробным населе­нием воспроизводит некоторые черты обитаемых природных во­доемов уже потому, что он сам является населенным водоемом, хотя и значительно меньших размеров. Одна из наиболее слож­ных проблем, с которой приходится сталкиваться при работе с реальными (натурными) моделями, заключается в трудности установления степени адекватности модели оригиналу и, следова­тельно, в обосновании возможности применения результатов мо­делирования к исходной системе-оригиналу. В отличие, например, от аэро- или гидродинамики, где разработаны количественные критерии адекватности моделей (критерий Рейнольдса и т.п.), в результате чего стало возможным успешное применение натур­ных моделей для решения широкого круга научных и конструк­торских задач в указанных областях, при натурном моделирова­нии экосистем вопросы обоснования адекватности еще очень да­леки от удовлетворительного решения. Кроме того, создание и использование натурных моделей экоси­стем связано с известными трудностями технического характера, преодоление которых, из-за отсутствия гарантий адекватности, отнюдь не всегда приводит к решению поставленной задачи.

В отличие от реальной, знаковая модель представляет собой условное описание системы-оригинала с помощью данного алфа­вита символов и операций над символами, и результате чего по­лучаются слова и предложения некоторого языка, которые с по­мощью определенного кода интерпретируются как образы некоторых свойств элементов системы-оригинала и связей между ними. Как отмечает И. А. Полетаев (1966), знаковые модели не­сравненно богаче возможностями, чем реальные, ибо они почти не связаны ограничениями физической реализации.

Наибольшее значение для экологии имеют две разновидности знаковых моделей: это, во-первых, так называемые концептуаль­ные и, во-вторых, математические модели.

Концептуальная модель представляет собой несколько более формализованный и систематизированный вариант традиционного естественнонаучного описания изучаемой экосистемы, состоящей из научного текста, сопровождаемого блок-схемой системы, табли­цами, графиками и прочим иллюстративным материалом. Не­сколько тавтологичный, но широко применяемый термин “концеп­туальная модель” подчеркивает, что назначение этой модели — служить ясным, обобщенным и в то же время достаточно полным выражением знаний и представлений исследователя об изучаемой системе в рамках и средствами определенной научной концепции. Например, в рамках “энергетической” или “биогеохимической” концепции соответствующие концептуальные модели принимают форму блок-схем трофических связей или потоков вещества в экосистеме, которые сопровождаются поясняющим текстовым, табличным и графическим материалом, раскрывающим состав, структуру и некоторые аспекты функционирования экосистемы.

В то же время наряду с такими общеизвестными достоинства­ми концептуальных моделей, как универсальность, гибкость, богатство средств выражения и др., благодаря которым этот метод применяется к самым разным системам, ему свойственны и недо­статки, как, например, высокая неоднозначность интерпретации и известная статичность, затрудняющая описание динамических си­стем.

При количественном изучении динамики экосистем гораздо более эффективны методы математического моделирования.

В качестве примера рассмотрим идеализированную систему, состоящую из одной популяции, которая существует в условиях изобилия корма и при отсутствии врагов и паразитов. Предполо­жим, что в этих условиях прирост популяции пропорционален до­стигнутой численности, причем удельная скорость прироста r за­висит от единственного внешнего фактора — температуры окру­жающей среды, которая на рассматриваемом промежутке времени t₀≤ t≤ t_N считается известной. Чтобы построить математическую модель такой системы, рассмотрим множество V, состоящее из одного элемента — входной функции v(t), задающей динамику температуры окружающей среды при t₀≤ t≤ t_N, а также множе­ство X, тоже состоящее из одного элемента, действительной пере­менной х(t), обозначающей численность популяции в момент вре­мени t. Структуру модели образуют три математических соотно­шения:

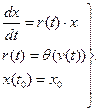(1)

Первое выражает линейную зависимость скорости роста попу­ляции от ее численности с меняющимся во времени коэффициен­том удельного прироста r(t). Второе служит математическим вы­ражением зависимости r от температуры окружающей среды v (функция 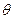(v) считается известной). Третье задает начальную численность популяции при t=t₀

Для нахождения функции модели, т. е. разрешающего опера­тора F системы (1), подставим в первое уравнение выраже­ние r через v с помощью функции 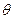(v):

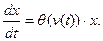(2)

Разделяя переменные:

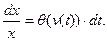(3)

и интегрируя от х₀ до х и от t₀ до t соответственно, где х₀=х(t₀) и х=х(t), получаем

ln|x|-ln|х₀|=и(v(t))dt (4)

После потенцирования получаем окончательный результат:

х(t)=х₀exp{ 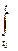и(v(t))dt} (5)

Таким образом, функционирование модели выражается опера­тором

х(t)=F(v,х₀,t)=х₀exp{ 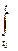и(v(t))dt} (6)

В зависимости от свойств разрешающего оператора F матема­тические модели динамичных систем классифицируются по раз­ным признакам. Так, если для оператора F найдено точное ана­литическое выражение, позволяющее для любых входных функ­ций и начальных условий непосредственно определять значение переменных состояния x₁,…,x_n в любой нужный момент t, то мо­дель принято называть аналитической. Аналитические модели об­ладают многими благоприятными свойствами, облегчающими их исследование и применение. Однако в подавляющем большинстве случаев нахождение аналитического выражения для разрешаю­щего оператора F оказывается затруднительным или в принци­пе невозможным. Процедуру численного решения этих уравнений на ЭВМ, в результате чего получается реализация оператора F в виде ма­шинной программы, с помощью которой по входным и начальным данным рассчитываются значения переменных состояний x₁(t),…,x_n (t) на интервале t₀≤t≤ t_N. Такие модели называются чис­ленными, или, чаще, имитационными.

В зависимости от степени определенности предсказания траек­тории (x₁(t),…,x_n (t)) оператором F модели делятся на детер­минированные и стохастические (вероятностные). Если в детер­минированной модели значения переменных состояния опреде­ляются однозначно (с точностью до ошибок вычисления) (рис. 2, А), то стохастическая модель для каждой переменной x_i, дает распределение возможных значений, характеризуемое та­кими вероятностными показателями, как математическое ожида­ние М{x_i}, среднее квадратическое отклонение σ(x_i) и т. п. (рис. 2, Б).

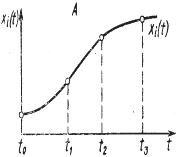
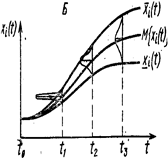
Рисунок 2. Детерминированная (А) и стохастическая (Б) модели динами­ки переменной x_i(t).

Для любого момента времени t де­терминированная модель предсказы­вает единственное значение пере­менной x_i(t), а стохастическая мо­дель показывает интервал [ x_i(t), x_i(t) ], содержащий величину x_i(t) и ее распределение на этом интерва­ле (в частности, математическое ожидание М{ x_i(t) }, среднее квадратическое отклонение σ{ x_i(t),} и дру­гие статистические показатели).

По характеру временного описания динамики переменных со­стояния x_i(t) различаются дискретные и непрерывные модели. Дис­кретная модель описывает поведение системы на фиксированной последовательности моментов времени t₀<t₁<…<t_i< t_N, тогда как в непрерывной модели значения переменных состояния могут быть рассчитаны для любой точки t рассматриваемого интервала [ t_0, t_N ]. Среди дискретных выделяются модели с фиксированным шагом по времени Δt= t_i-t_i-1, который не может быть изменен без глубокой перестройки всей мо­дели. Например, в моделях ди­намики популяции организмов с непрерывающимися поколения­ми, сменяющимися только один раз в год, принимается Δt= 1 год (Варли, Градуэлл,Хасселл, 1978). В отличие от них существуют дискретные модели, в которых шаг по времени Δt может неогра­ниченно уменьшаться (в преде­лах возможностей используемой ЭВМ), вследствие чего такие мо­дели по детальности описания временных изменений приближа­ются к непрерывным. В частно­сти, таковы модели, получающи­еся в результате дискретизации непрерывного описания изу­чаемой системы в процессе приближенного численного ре­шения дифференциальных урав­нений.

Следующий важный признак, которому различаются математические модели экосистем, - это характер описания их про­странственного строения. Моде­ли, в которых пространственное строение экосистемы не рассмат­ривается, т. е. в качестве пере­менных состояния фигурируют зависящие только от времени пе­ременные x_i(t),..., n, принято называть моделями с сосредо­точенными значениями (или точечными моделями), в отличие от моделей с распределенными значениями, в которых переменные состояния x_i зависят не только от времени, но и от пространствен­ных координат (одной или нескольких). Например, при модели­ровании водной экосистемы в качестве переменных состояния можно взять усредненные по площади и суммированные по глу­бине значения биомасс популяций, запасов биогенных элементов и т. д., выраженные, например, в граммах под площадью зеркала воды в 1 м² — это будет модель с сосредоточенными значениями (Алексеев, 1975). Если в модели учитывается гетерогенность по глубине (координата z), т. е. x_i=x_i(z,t) то получается (очевид­но, более детальная) модель с распределенными значениями по глубине, но все еще осредненными по плоскости (х, у). При опи­сании мелкого, хорошо перемешиваемого по вертикали, но гете­рогенного по плоскости водоема целесообразно в качестве пере­менных состояния использовать функции вида x_i=x_i(x,y,t). Наконец, вводя все три пространственные координаты x_i=x_i(x,y,z,t), получают модель с пространственно распределен­ными значениями.

Завершая краткое введение в метод моделирования, остано­вимся на некоторых способах визуального представления резуль­татов моделирования. Наиболее часто используется так называе­мый способ развертки во времени, который состоит в построении таблиц или графиков изменения входных переменных и перемен­ных состояния как функций времени t (рисунок 3,A). При всех его достоинствах этот способ не всегда (особенно при большом числе переменных) дает наглядное представление взаимосвязей между переменными. Поэтому в дополнение к нему нередко ис­пользуется так называемый способ фазовых портретов, когда на график наносится изображение траектории системы в простран­стве состояний (при n=2 или 3) или проекции этой траектории на координатные плоскости (x_i, x_j), образованные различными парами координат при n>3 (рисунок 3, Б). Время присутствует на фазовом портрете неявно, через указание тем или иным спо­собом направления движения изображающей точки вдоль траек­тории (например, с помощью стрелок или отметок времени вдоль траектории). Соотношение способов развертки во времени и фазового портрета поясняет рисунок 3, В).

Рисунок 3 - Представление результатов моделирования способами развертки по времени (А) и фазового портрета (Б), соотношение этих двух способов в случае двухмерного фазового пространства (В).

В качестве примера рассмотрим простейшее дифференциальное уравнение, описывающее рост популяции какого-либо вида:

dх/dt=rх,

где х — плотность популяции в момент времени t; r — истинная скорость роста, принятая постоянной. Решением этого уравнения является функция

х=х₀е^rt,

где х₀ — плотность популяции в момент време­ни t=0.

Следовательно, если проводить наблюдение за большой выборкой особей в течение короткого периода времени Δt, то доля особей, размножившихся в течение этого периода, бу­дет равна rΔt. Значит, возрастной состав попу­ляции не изменяется во времени. Но это спра­ведливо лишь для ограниченного периода вре­мени, так как возрастная структура популяции будет приближаться к устойчивой лишь тогда, когда специфичные для каждой возрастной группы рождаемость и смертность остаются постоянными. Такого состояния популяция мо­жет достичь только при постоянстве условий среды, избытке необходимых ресурсов и отсут­ствии эволюционных процессов (изменений). Но в естественных условиях этого никогда не на­блюдается. Как видно, при отсутствии реальных моделей математический подход становится все более отвлеченным. При исключении же математиче­ского подхода часто бывает трудно уловить общий смысл реальной модели. Вот почему в современной экологии реальные и знаковые модели используются параллельно, дополняя и обогащая друг друга. Первыми математическими моделями про­стейших экологических систем хищник — жер­тва и паразит — хозяин были теоретические разработки В. Вольтерры, сделанные в 1931 г. Они послужили толчком для по­строения более сложных моделей процессов пищевых отношений популяций в биоценозах. С появлением быстродействующих электронно-вычислительных машин возникли возможности моделирования еще более сложных саморегу­лирующихся систем с обратной связью — попу­ляций, биоценозов и биогеоценозов. На основе математического моделирования успешно изучаются микробные популяции и по­пуляции одноклеточных водорослей, выращиваемых в культиваторах, исследуются явления внутривидовой конкуренции и различные фор­мы межвидовых взаимоотношений. Важное ме­сто занимает попытка математического моде­лирования в экологических исследованиях, на­правленных на использование ресурсов при­роды так, чтобы в ней осуществлялось есте­ственное их самовоспроизводство. Для этого нужно не только знать сущность основных вза­имодействий и процессов, протекающих в биогеоценозах, в биосфере в целом, но и с помощью математических методов прогнозиро­вать их хотя бы на ближайшее будущее.

В современных условиях моделирование занимает основное место в работах по эко­логическому прогнозированию. Как отмечает А. А. Ляпунов, «задачи изучения математиче­ских моделей биогеценозов состоят в том, что­бы сопоставить кинетику явлений, подсказываемую моделью, с той, которая наблюдается в действительности, и, опираясь на это сопостав­ление, довести модель до достаточно хорошего согласия с действительностью. Тогда такие мо­дели станет возможным использовать для прак­тических прогнозов, а также для выбора ра­ционального вмешательства человека в жизнь природы, с тем чтобы обеспечить такое исполь­зование природных ресурсов, при котором бы они должным образом самовоспроизводи­лись». В основу математического моделирования при экологическом прогнозировании положен принцип представления сложной биологической системы в виде отдельных подсистем (блоков, модулей, камер), связанных между собой фун­кциональными связями, имитирующими либо поток веществ (в том числе и загрязняющих), либо регулирующиеся воздействия, либо про­странственные миграции, либо развитие орга­низмов и т. д.

Например, в водной экосистеме выделяются как отдельные подсистемы: рыбы разного воз­раста, разные виды фитопланктона, зоопланк­тона, бентос, донные отложения, поступающие в водоем стоки и т. д. Кроме того, можно выделять и функциональные зависимости: пло­довитость рыб в норме и при определенных воздействиях, например свинца или других ве­ществ; плодовитость и продолжительность жиз­ни фито- и зоопланктона, бентоса; зависимость от температуры среды выклевывания мальков из икры, времени нереста и т. д. При этом экологический прогноз с помощью математиче­ских моделей возможен только при наличии данных о «нулевой точке отсчета», т. е. о не нарушенной природой системе. В последние годы среди прогнозистов широ­ко распространилось понятие «мониторинг», которое было предложено еще в 1920-х гг. по отношению к окружающей среде. Часто за мониторингом признается только наблюдение за состоянием окружающей среды. В более широком смысле в понятие «мониторинг» вклю­чают не только наблюдение, а также контроль и управление состоянием окружающей среды, т. е. то или иное целенаправленное воздействие на нее. Таким образом, мониторинг слагается из двух последовательных этапов: от наблюде­ния до контроля и управления. Ограничение мониторинга наблюдением придает ему лишь пассивное, информационное значение. Задачей современного мониторинга является прогноз. Программа фонового экологического мони­торинга реализуется в биосферных заповедни­ках. Схема фонового мониторинга загрязнения при­родной среды и его экологических последствий четко подразделяется на геохимический, геофизический и биологический мониторинги. Цель биохимического и геофизического мониторингов — получение информации об уров­не загрязнения окружающей среды, об интен­сивности и характере воздействий загрязнения на биологические системы, а также прогнозиро­вание уровней загрязнения биоты в будущем. Цель биологического мониторинга — оценка и прогноз реакции экосистем в ответ на фоно­вые воздействия загрязнителей. В его основу положены разработки математических моде­лей экосистем, которые могли бы служить ин­струментом прогнозов изменения состояния экосистем на фоновом глобальном уровне. Та­кие модели позволяют строить прогнозы о том, когда и под влиянием каких уровней воздействия загрязнителей исчезнут наиболее чувствитель­ные к загрязнениям виды, установить очеред­ность их исчезновения или существенного сни­жения численности популяций в той или иной экосистеме. Примером успешного применения матема­тической модели для прогнозирования является разработанная В. В. Меншуткиным модель ди­намики численности лососевых рыб. Анализ мо­дели на ЭВМ позволил выяснить и понять важнейшие закономерности жизнедеятельности камчатской нерки. На модели был проведен ряд экспериментов. В результате установили, что на нерестилищах нерки наблюдается повы­шенная смертность мальков, а в открытом мо­ре катастрофически возрос промысел лососей. Модель явилась официальным документом при составлении прогноза. Ограничения вылова ло­сосей в открытом море позволили сохранить стадо этих ценных рыб. В настоящее время модели чаще всего используются для решения конкретных сегодняшних задач: применять или не применять пестициды, какую природную среду требуется контролировать в первую очередь, какие антропические нагрузки допустимы и т. д. Хотя все эти сегодняшние проблемы невозможно решать без обоснованного прогноза на далекую перс­пективу.

Лекция № 4

Дата добавления: 2014-11-06