Основная лемма статики

УСЛОВИЯ РАВНОВЕСИЯ. УСЛОВИЯ РАВНОВЕСИЯ В ОБЩЕМ И ЧАСТНЫХ СЛУЧАЯХ

Обобщенная теорема Вариньона

Теорема. Если система сил имеет равнодействующую, то момент этой равнодействующей относительно некоторого полюса равен геометрической сумме моментов всех сил системы относительно того же полюса.

Теорема. Если система сил имеет равнодействующую, то момент этой равнодействующей относительно некоторой оси равен алгебраической сумме моментов всех сил системы относительно той же оси.

Леммой называют теорему, необходимую только для доказательства другой теоремы.

Лемма. Любая система сил эквивалентна системе из двух сил, то есть любая система сил с помощью элементарных операций может быть приведена к двум силам.

Доказательство.

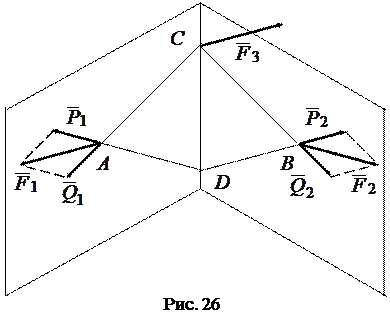Предварительно докажем лемму для трех сил , , .

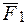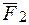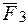Проведем две плоскости (рис. 26); одну через силу 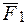и точку 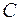, вторую через силу 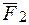и ту же точку .

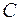Эти плоскости, имея общую точку 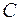, имеют общую прямую. На этой прямой выберем произвольную точку 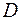и соединим точк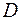и и 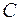прямыми с точкам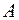и и 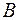, в которых приложены силы 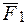и 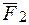. Разложим силы 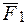и 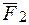на составляющие по проведенным направлениям: ,

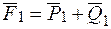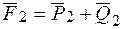. Перенесем силы 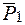и 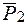по их линиям действия в точку 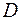, а силы 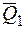и 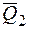в точку 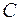(рис. 27). В результате получим две системы сходящихся сил:{ 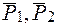} и { .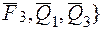

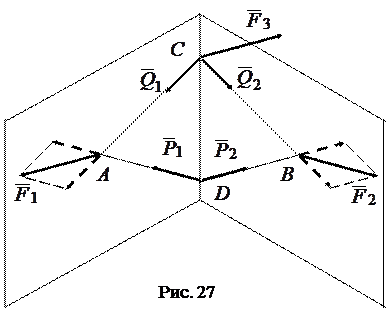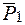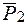Заменяем силы и , приложенные в точке 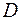, их геометрической суммой 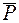, приложенной в той же точке: 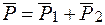, а силы 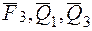, приложенные в точке 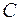– силой 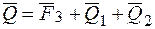, приложенной так же в точке 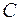. В результате применения только элементарных операций система сил { 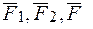} приведена к двум силам { 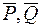}. Итак, заданная система сил { 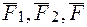} эквивалентна двум силам { }:

{ }~{ },

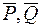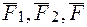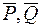что и требовалось доказать.

Если задана система, состоящая из 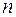сил, то тогда, последовательно заменяя каждые три силы двумя, уменьшаем число сил системы. Процесс заканчивается, когда остается только три силы.

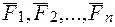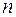{ } — сил

{ } —сил

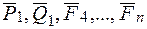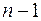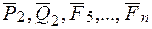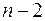{ } —сил

…… …

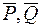{ } —силы

Дата добавления: 2014-11-06