Ol — V2X 41 страница

Таким образом, три коэффициента п, £, х, фигурирующие в системе уравнений движения вязкой теплопроводящей жидкости, полностью определяют гидродинамические свойства жидкости в рассматриваемом, всегда применяемом приближении (т. е. при пренебрежении производными высших порядков по координа­там от скорости, температуры и т. п.). Введение в уравнения каких-либо дополнительных членов (например, введение в плот­ность потока массы членов, пропорциональных градиентам плот­ности или температуры) лишено физического смысла и означало бы в лучшем случае лишь изменение определения основных ве­личин; в частности, скорость не совпадала бы с импульсом еди­ницы массы жидкости¹).

§ 50. Теплопроводность в несжимаемой жидкости

Общ,ес уравнение теплопроводности в форме (49,4) или (49,5) может быть в различных случаях значительно упрощено.

Если скорость движения жидкости мала по сравнению со ско­ростью звука, то возникающие в результате движения изменения давления настолько малы, что вызываемым ими изменением плотности (и других термодинамических величин) можно пре­небречь. Однако неравномерно нагретая жидкость не является все же при этом вполне несжимаемой в том смысле, как это понималось выше. Дело в том, что плотность меняется еще и под влиянием изменения температуры; этим изменением плотности, вообще говоря, нельзя пренебречь, и потому даже при доста­точно малых скоростях плотность неравномерно нагретой жид­кости все же нельзя считать постоянной. При определении про­изводных от термодинамических величин в этом случае надо, следовательно, считать постоянным давление, а не плотность. Так, имеем:

di (ds \ дТ _ / ds \ _„

и поскольку Т^-^г^ есть теплоемкость с_р при постоянном дав­лении, то

') В худшем же случае введение таких членов может вообще нарушить соблюдение необходимых законов сохранения. Следует иметь в виду, что при любом определении величин плотность потока массы j во всяком случае должна совпадать с импульсом единицы объема жидкости. Действительно, плотность потока j определяется уравнением непрерывности

f- + divj = 0;

умножая его на г и интегрируя по всему занятому жидкостью объему, получим:

а поскольку интеграл J pr dV определяет положение центра инерции данной массы жидкости, то ясно, что интеграл ^ ] dV есть ее импульс.

Уравнение (49,4) принимает вид

Р^ср йг + ^{v vr}) ^{= dlv (х vr)} + <k j%• (60,1)

Для того чтобы в уравнениях движения неравномерно на­гретой жидкости можно было считать плотность постоянной, не­обходимо (помимо малости отношения скорости жидкости к ско­рости звука), чтобы имеющиеся в жидкости разности температур были достаточно малы; подчеркнем, что здесь речь идет именно об абсолютных значениях разностей температур, а не о гра­диенте температуры. Тогда жидкость можно считать несжимае­мой в том же смысле, как это подразумевалось раньше; в ча­стности, уравнение непрерывности будет выглядеть просто как divv = 0. Считая разности температур малыми, мы будем пре­небрегать также и температурным изменением величин л, к, c_Pt

, dv,

т. е. будем считать их постоянными. Написав член a_ik -jj- в том

виде, как это сделано в (49,5), мы получим в результате уравне­ние переноса тепла в несжимаемой жидкости в следующем срав­нительно'простом виде:

дТ v / dv. dv.\²

_ + v ут ~ _% AT + ^JL +, (60,2)

где v = п/р — кинематическая вязкость, а вместо х введена тем­пературопроводность

% = фс_р. (50,3)

В особенности просто выглядит уравнение переноса тепла в неподвижной жидкости, где перенос энергии обязан целиком теп­лопроводности. Опуская в (50,2) члены, содержащие скорость, получаем просто

1Г = ХДГ. (50,4)

Это уравнение называется в математической физике уравнением теплопроводности или уравнением Фурье. Оно может быть вы­ведено, разумеется, и гораздо более простым образом, без по­мощи общего уравнения переноса тепла в движущейся жидко­сти. Согласно закону сохранения энергии количество тепла, по­глощающееся в некотором объеме в единицу времени, должно быть равно полному потоку тепла, втекающего в этот объем че­рез ограничивающую его поверхность. Как мы знаем, такой за­кон сохранения может быть выражен в виде уравнения непре­рывности для количества тепла. Это уравнение получается при­равниванием количества тепла, поглощающегося в единице объе­ма жидкости в единицу времени, дивергенции плотности потока тепла, взятой с обратным знаком. Первое из них равно рс_р-^-\

здесь'должна быть взята теплоемкость с_р, так как вдоль непод­вижной жидкости давление должно быть, разумеется, постоян­ным. Приравняв это выражение — divq = хД7, получим как раз уравнение (50,4).

Необходимо отметить, что применимость уравнения тепло­проводности (50,4) к жидкостям практически сильно ограничена. Дело в том, что в жидкостях, реально находящихся в поле тя­жести, уже малый градиент температуры приводит в большин­стве случаев к возникновению заметного движения (так назы­ваемая конвекция; см. § 56). Поэтому реально можно иметь дело с неравномерным распределением температуры в неподвижной жидкости, разве только, если градиент температуры направлен противоположно силе тяжести или же если жидкость очень вяз­кая. Тем не менее, изучение уравнения теплопроводности в фор­ме (50,4) весьма существенно, так как уравнением такого вида описываются процессы теплопроводности в твердых телах. Имея это в виду, мы займемся здесь и в §§ 51, 52 более подробным его исследованием.

Если распределение температуры в неравномерно нагретой неподвижной среде поддерживается (посредством некоторых внешних источников тепла) постоянным во времени, то уравне­ние теплопроводности принимает вид

Д7==0. (50,5)

Таким образом, стационарное распределение температуры в не­подвижной среде описывается уравнением Лапласа. В более общем случае, когда коэффициент к нельзя считать постоянным, вместо (50,5) имеем уравнение

div(xV7) = 0. (50,6)

Если в жидкости имеются посторонние источники тепла, то к уравнению теплопроводности должен быть добавлен соответ­ствующий дополнительный член (таким источником тепла мо­жет, например, являться нагревание электрическим током). Пусть Q есть количество тепла, выделяемое этими источниками в еди­нице объема жидкости в единицу времени; Q является, вообще говоря, функцией от координат и от времени. Тогда условие ба­ланса тепла, т. е. уравнение теплопроводности, напишется в виде

p_Cp4f= *^Ar + Q- (50,7)

Напишем граничные условия для уравнения теплопровод­ности, которые должны иметь место на границе двух сред. Прежде всего, на границе должны быть равными температуры обеих сред:

Т\ = Г_а. (50,8).

Кроме того, поток тепла, выходящего из одной среды, должен быть равен потоку, входящему во вторую среду. Выбирая си­стему координат, в которой данный участок границы покоится, можно написать это условие в виде

%х VT_xd\ = и₂уГ₂ di для каждого элемента df поверхности раздела. Написав

VTdf^^df,

где дТ/дп — производная от Т по направлению нормали к по­верхности, получим граничное условие в виде

*'-лГ = *2-лГ- <⁵⁰>⁹>

Если на поверхности раздела имеются посторонние источники тепла, выделяющие количество тепла Q^(s) на единице площади в единицу времени, то вместо условия (50,9) надо написать:

*-Ж-*>%Г = <*^Л- <⁵⁰>¹⁰>

В физических задачах о распределении температуры при наличии источников тепла интенсивность последних обычно сама задается в виде функции температуры. Если функция Q(T) до­статочно быстро возрастает с увеличением Т, то установление стационарного распределения температуры в теле, границы ко­торого поддерживаются при заданных условиях (например, при заданной температуре), может оказаться невозможным. Тепло-отвод через внешнюю поверхность тела пропорционален неко­торому среднему значению разности температур Т — Т₀ тела и внешней среды вне зависимости от закона тепловыделения внут­ри тела. Ясно, что если последнее достаточно быстро возрастает с температурой, то теплоотвод может оказаться недостаточным для осуществления равновесного состояния.

В этих условиях может возникнуть тепловой взрыв: если ско­рости экзотермической реакции горения достаточно быстро воз­растают с температурой, то при невозможности стационарного распределения возникают быстрое нестационарное разогревание вещества и ускорение реакции (Н. Н. Семенов, 1923). Скорость (а с ней и интенсивность выделения тепла) взрывных реакций горения зависит от температуры в основном пропорционально множителю ехр(—И/Т) с большой энергией активации U. Для исследования условий возникновения теплового взрыва следует рассматривать ход реакции при сравнительно незначительном разогревании вещества и соответственно этому разложить

1 1 Т—т_п

где Го — внешняя температура. Таким образом, задача сводится к исследованию уравнения теплопроводности с объемной интен­сивностью источников тепла вида

Q = Q₀exp{a(T — Т₀)} (50,11)

(Д. А. Франк-Каменецкий, 1939), — см. задачу 1.

Задачи

1. В слое вещества между двумя параллельными плоскостями распре-
делены источники тепла с объемной интенсивностью (50,11). Граничные пло-
скости поддерживаются при постоянной температуре. Найти условие, опреде-
ляющее возможность установления стационарного распределения температуры
(Д. А Франк-Каменецкий, 1939) ').

Решение. Уравнение стационарной теплопроводности в данном случае гласит:

с граничными условиями Т = То при к — 0 и х = 21 (21 — ширина слоя). Вводим безразмерные переменные т = а(Т — Го) и | = *//; тогда

Интегрируя это уравнение (умножив его на 2т') один раз, найдем;

т" = 2Л,(е*-е^г),

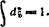
где г» — постоянная. Последняя представляет собой, очевидно, максимальное значение т, которое ввиду симметрии задачи должно достигаться посередине слоя, т.е. при |=1. Поэтому вторичное интегрирование с учетом условия т = 0 при £ = 0 дает

То 1

1 С dx

V2l J л/е^х> - е^х о ^v

Произведя интегрирование, получим

Arched- (1)

Определяемая этим равенством функция \(т₀) имеет максимум X — %_кр при определенном значении То = То «р; если А, > Акр, то удовлетворяющего гранич­ным условиям решения не существует²). Численные значения: А*_Р = 0,88, Токр = 1,2 ^s).

¹) Подробное изложение относящихся сюда вопросов см. в книге: Франк- Каменецкий Д. А Диффузия и теплопередача в химической кинетике. — М.: Наука, 1967. ²) Из двух корней уравнения (1) при А < А_кр устойчивому распределе- нию температуры соответствует лишь меньший. ³) Аналогичные значения для сферической области (с ее радиусом в ка- честве длины I) равны tap = 3,32, т_{0 кр} = 1,47, а для бесконечного цилиндра Якр =- 2,00 т₀кр — 1,36.

2. В неподвижную жидкость, в которой поддерживается постоянный гра-
диент температуры, погружен шар. Определить возникающее стационарное
распределение температуры в жидкости и шаре.

Решение. Распределение температуры определяется во всем простран­стве уравнением ДГ = 0 с граничными условиями

Г Т v ^dTl - * ^дТ*

при г = R (R — радиус шара; величины с индексами 1 и 2 относятся соот­ветственно к шару и жидкости) и условием V7" = А на бесконечности (А — заданный градиент температуры). В силу симметрии условий задачи А есть единственный вектор, которым должно определяться искомое решение. Та­кими решениями уравнения Лапласа являются const Аг и const AV(l/r). За­мечая, кроме того, что решение должно оставаться конечным в центре шара, ищем температуры 7\ и Т₂ в виде

Г! = с,Аг, Т₂ = с₂А + Аг;

постоянные Ci и с₂ определяются из условий при г = R, и в результате находим:

Зх₂

К\ + 2и₂

§ 51. Теплопроводность в неограниченной среде

Рассмотрим теплопроводность в неограниченной неподвижной среде. Наиболее общей постановкой задачи является следующая. В начальный момент времени t = 0 задано распределение тем­пературы во всем пространстве:

Т = Т₀(т) при / = 0,

где Го (г) — заданная функция координат. Требуется определить распределение температуры во все последующие моменты вре­мени.

Разложим искомую функцию Г (г, г) в интеграл Фурье по ко­ординатам:

Т(г,Ц~\т_ка)е**.**г, Г* (0==$ Г (г,(61,1)

Для каждой фурье-компоненты температуры, 7'_ke'^kr, уравнение (50,4) дает:

^■ + №=0,

откуда находим зависимость 7_к от времени:

Гк-Гокб-^'.

Поскольку при г = 0 должно быть Т = Т₀(г), ТО ЯСНО, ЧТО Г₀к представляет собой коэффициенты фурье-разложения функции Т₀:

r_№=$7^,o(r^,)e-^|kr'd^sJt^/.

Таким образом, находим:

Т = ^ Г₀(г') е-^k'*^fe^ik <'-''>d³x'-^d'^k

(2я)³ •

Интеграл по d³k разбивается на произведение трех одинаковых интегралов вида

Je-«5^!cospgdg = (^-)'^/2e-P^!'^ta

где §— одна из компонент вектора к (аналогичный интеграл с sin вместо cos исчезает в силу нечетности функции sin). В ре­зультате получаем окончательно следующее выражение:

^т(г'^/}=Т^г\ ^т° ^(г'^{} ех}Р { - ^} ^йЧ- ⁽⁵¹ "²>

Эта формула полностью решает поставленную задачу, опре­деляя распределение температуры в любой момент времени по ее заданному распределению в начальный момент.

Если начальное распределение температуры зависит только от одной координаты х, то, произведя в (51,2) интегрирование по dy'dz', получим:

со

^т{х> <>-чщ^S^г° ⁽*'^{} ехр} {- -^г¹¹}^dx'- ⁽⁵¹'³⁾

— оо

Пусть при t = 0 температура равна нулю во всем простран­стве, за исключением одной точки (начала координат), в кото­рой она принимает бесконечно большое значение, но так, что

полное количество тепла, пропорциональное интегралу ^ Г₀(г) d³x,

остается конечным. Такое распределение можно представить б-функцией:

Г₀ (г) = const-б (г). (51,4)

Интегрирование в формуле (51,2) сводится тогда просто к за­мене г' нулем, в результате чего получается:

Г (г, t) = const * e-"i*#. (51,5)

8 (n%t) '

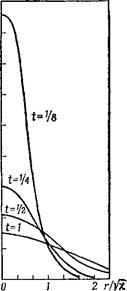
С течением времени температура в точке г = 0 падает как t~³¹². Одновременно повышается температура в окружающем про­странстве, причем область заметно отличной от нуля темпера­туры постепенно расширяется (рис. 39). Ход этого расширения определяется в основном экспоненциальным множителем в (51,5): порядок величины / размеров этой области дается выражением

/~Ух7, (51.6)

т. е. растет пропорционально корню из времени.

Аналогично, если в начальный момент времени конечное количество тепла сконцентрировано в плоскости х = О, то в по­следующее время распределение темпе­ратуры определится формулой

Т(х, /)= const ' е-*¹**. (51,7) 2 (яхО '

Формулу (51,6) можно истолковать с несколько иной точки зрения. Пусть I есть порядок величины размеров тела. Тогда можно утверждать, что если это тело было неравномерно нагрето, то по­рядок величины времени т, в течение ко­торого температуры в разных точках тела заметно выравнятся, равен

т~/7х- (51,8)

Время т, которое можно назвать време­нем релаксации для процесса теплопро­водности, пропорционально квадрату раз­меров тела и обратно пропорционально коэффициенту температуропроводности.

Процесс теплопроводности, описывае-
мый полученными здесь формулами, об-
ладает тем свойством, что влияние вся- Рис. 39
кого теплового возмущения распростра-
няется мгновенно на все пространство. Так, из формулы (51,5)
видно, что тепло из точечного источника распространяется так,
что уже в следующий момент времени температура среды обра-
щается в нуль лишь асимптотически на бесконечности. Это
свойство сохраняется и для среды с зависящей от температуры
температуропроводностью если только эта зависимость не
приводит к обращению % в нуль в какой-либо области простран-
ства. Если же 1 есть функция температуры, убывающая и обра-
щающаяся в нуль вместе с нею, то это приводит к такому за-
медлению процесса распространения тепла, в результате кото-
рого влияние любого теплового возмущения будет простираться
в каждый момент времени лишь на некоторую конечную об-
ласть пространства; речь идет о распространении тепла в среду,
температуру которой (вне области влияния) можно считать
равной нулю (Я. Б. Зельдович, А, С. Компанеец, 1950; им же
принадлежит решение приведенных ниже задач).

Задачи

1. Теплоемкость и теплопроводность среды — степенные функции темпе-
ратуры, а ее плотность постоянна. Определить закон обращения температуры
в нуль вблизи границы области, до которой в данный момент распространя-
лось тепло из некоторого произвольного источника; вне этой области темпе-
ратура равна нулю.

Решение. Если х и с„ — степенные функции температуры, то то же самое относится к температуропроводности % и к тепловой функции

w =^c_pdT (постоянный член в w опускаем). Поэтому можно написать

X = aW", где посредством W = pw мы обозначили тепловую функцию еди­ницы объема среды. Тогда уравнение теплопроводности

рср-Ц—dlv(xvT)

приобретет вид

^j-=adiv (WⁿW). (1)

В течение небольшого интервала времени малый участок границы можно считать плоским, а скорость его перемещения в пространстве v — постоянной. Соответственно этому ищем решение уравнения (1) в виде W = W(x — vt), где х — координата в перпендикулярном к границе направлении. Имеем:

откуда после двукратного интегрирования находим следующий закон обраще­ния W в нуль:

Wco\x\^Vn, (3)

где \х\ — расстояние от границы нагретой области. В то же время этим под­тверждается вывод о наличии границы нагретой области (вне которой W, а с ней и Т равны нулю), если показатель п > 0. Если п г=: 0, то уравнение (2) не имеет решений, обращающихся в нуль на конечном расстоянии, т. е. тепло распределено в каждый момент по всему пространству.

2. В той же среде в начальный момент времени в плоскости к = 0 скон-
центрировано количество тепла, равное (будучи отнесено к единице площа-
ди) Q, а в остальном пространстве Т — 0. Определить- распределение темпе-
ратуры в последующие моменты времени.

Решение. В одномерном случае уравнение (1) гласит:

Из имеющихся в нашем распоряжении параметров Q и а и переменных х t можно составить лишь одну безразмерную комбинацию:

(Q и а имеют размерность соответственно эрг/см² и см²/сек (см³/эрг)^п). По­этому искомая функция W(x, I) должна иметь вид где безразмерная функция?(|) умножена на величину, имеющую размер­ность эрг/см³. После этой подстановки уравнение (4) дает

«+*£(''3)+«i+'-»

Это уравнение в полных производных имеет простое решение, удовлетворяю­щее условиям задачи:

где So — постоянная интегрирования.

При п > 0 эга формула дает распределение температуры в области ме­жду границами х = ±х₀, определяющимися равенством £ = ±£о", вне этих границ W = 0. Отсюда следует, что границы нагретой области расширяются со временем по закону

*„ - const f^1/(2+">.

Постоянная go определяется условием постоянства полного количества тепла:

Q= J Wdx = Q J f(l)dl, (8)

-*> -So

откуда получается

(9)

_)I+„₂,_„ r*(_ + _)

,24-11 (2 +Я)'

⁶⁰ пя"^/2 Г»(1/п) '

При п = —V < 0 напишем решение в виде

П1) = [у^(_£? + 1²)]^_1/". (Ю)

Здесь тепло распределено по всему пространству, причем на больших рас­стояниях W убывает по степенному закону: W ~ x~^2,v. Это решение приме­нимо лишь при v < 2; при v:> 2 нормировочный интеграл (8) (который бе­рется теперь в пределах ±оо) расходится, что физически означает мгновен­ный уход тепла на бесконечное расстояние. При v < 2 постоянная |₀ в (10) равна

_rv f'J_ _ 1\
₂__v 2(2-v)3t^v/2 U 2)
_h - -._rv_(1/v) • ОО

Наконец, при л -*- 0 имеем g₀ -> 2/У«и решение, определяемое форму­лами (5—7), дает

п-*о (2 -vW V 4аг/ J 2-vW в согласии с формулой (51,7).

§ 52. Теплопроводность в ограниченной среде

В задачах о теплопроводности в ограниченной среде задание начального распределения температуры недостаточно для одно­значности решения, и необходимо еще задание краевых условий на ограничивающей среду поверхности.

Рассмотрим теплопроводность в полупространстве (х > 0) и начнем со случая, когда на граничной поверхности х = 0 под­держивается заданная постоянная температура. Эту температуру мы примем условно за нуль, т. е. будем отсчитывать от нее тем­пературу в других точках среды.

В начальный момент времени по-прежнему задано распреде­ление температуры во всей среде. Таким образом, граничные и начальные условия гласят:

Г = 0 при х = 0; T = T₀(x,y,z) при f = 0, х > 0. (52,1)

Решение уравнения теплопроводности с этими условиями можно свести к решению того же уравнения для среды, не огра­ниченной в обоих направлениях оси х, при помощи следующего искусственного приема. Представим себе, что среда распростра­няется и по левую сторону от плоскости х— 0, причем в началь­ный момент времени распределение температуры в этой части среды описывается той же функцией Г₀, но только взятой с об­ратным знаком. Другими словами, в начальный момент времени распределение температуры во всем пространстве описывается некоторой функцией, нечетной по переменной х, т. е. такой, что

Го (—х, у, z) = —Го (х, у, z). (52,2)

Из равенства (52,2) следует, что Г₀(0, у, z)——Т₀(0, у, z) = 0, т. е. требуемое граничное условие (52,1) автоматически выпол­нено в начальный момент времени, и из симметрии условий за­дачи очевидно, что оно будет выполнено и во всякий другой мо­мент времени.

Таким образом, задача свелась к решению уравнения (50,4) в неограниченной среде с начальной функцией Г₀(х, у, г), удов­летворяющей (52,2), и без какого бы то ни было граничного условия. Поэтому мы можем воспользоваться общей формулой (51,2).

Разобьем в (51,2) область интегрирования по dx' на две части: от —оо до 0 и от 0 до со, и воспользуемся соотношением (52,2). Мы получим тогда:

оо оо

^хN{"^TJr¹¹}^_ехрЬ "У)]^dx'^d«'^dz'- <⁵²'³>

Эта формула полностью решает поставленную задачу, опреде­ляя температуру во всей среде.

Если начальное распределение температуры зависит только от х, то формула (52,3) принимает вид

о

-^exp{-^J£tr¹}]^- <⁵²'⁴⁾

В качестве примера рассмотрим случай, когда в начальный момент везде, кроме х = 0, температура равна заданной постоян­ной величине, которую, не ограничивая общности, можно поло­жить равной — 1; температура же на плоскости х = 0 все время равна нулю. Соответствующее решение получается непосред­ственно подстановкой Т₀(х) = —1 в (52,4). Разобьем интеграл в (52,4) на два интеграла и в каждом из них произведем за­мену переменных типа

х' — х ^

Тогда мы получим для Т(х, t) следующее выражение:

^•<>-iM-T7irH^rf(w)}'

где функция erf х определяется как

X

erf х==—~[e-l'dl (52,5)

Л/я J

о

и называется интегралом Ошибок (заметим, что erf(oo) = ^.По­скольку

erf (—х) = — erf(x), то мы получаем окончательно:

На рис. 40 изображен график функции erf g. С течением времени распределение температуры по пространству все более сглажи­вается. Это сглаживание происходит таким образом, что каж­дое заданное значение температуры перемещается вправо про­порционально -\/'t. Последний результат, впрочем, заранее оче­виден. Действительно, рассматриваемая задача определяется всего одним параметром — начальной разностью температур Г₀ граничной плоскости и остального пространства (положенной выше условно равной единице). Из имеющихся в нашем распо­ряжении параметров Го и % и переменных х и t можно составить всего одну безразмерную комбинацию x/-\/%t; поэтому ясно, что искомое распределение температуры должно определяться функ­цией вида T = T₀f{xl-\/%t).

Рассмотрим теперь случай, когда граничная поверхность среды теплоизолирована. Другими словами, на плоскости * = 0

О 0,4 0,8 ],2 1,в 2Д

Рис. 40

тепловой поток должен отсутствовать, т. е. должно быть дТ/дх = 0. Таким образом, имеем теперь следующие граничные и начальные условия:

|^ = 0 при х = 0; Т = Т₀(х, у, г) при t = 0, х>0. (52,7)

Для нахождения решения поступим аналогично тому, как мы делали в предыдущем случае. Именно, опять представим себе среду неограниченной в обе стороны от плоскости х = 0. Распре­деление же температуры в начальный момент времени предста­вим себе теперь симметричным относительно плоскости х — 0. Другими словами, функцию Т₀(х, у, г) предположим теперь четной по переменной х:

Т₀{-х,у,г) = Т₀(х,у,г). (52,8)

Тогда

дТ₀ (х, у, z) ₌ дТ₀ (- х, у, г)
дх дх

и при jc = 0 будет дТо/дх = 0. Из симметрии очевидно, что это условие автоматически будет выполнено и во все последующие моменты времени. Повторив произведенные выше вычисления, но используя при этом (52,8) вместо (52,2), найдем, что общее решение поставленной задачи дается формулами, отличающи­мися от (52,3) или (52,4) лишь тем, что вместо разности двух членов в квадратных скобках стоит их сумма.

Перейдем к задачам с другого рода граничными условиями, тоже допускающими решение уравнения теплопроводности в об­щем виде. Рассмотрим среду, ограниченную плоскостью х = 0, через которую извне подводится поток тепла, являющийся за­данной функцией времени. Другими словами, имеем граничные и начальные условия:

— и-ц- —<7(0 при * = 0; Г = 0 при / = — оо, _х > О, (52,9)

где q(t) — заданная функция.

Предварительно решим вспомогательную задачу, в которой q(t) = 8(t). Легко сообразить, что эта задача физически экви­валентна задаче о распространении тепла в неограниченной среде от точечного источника, содержащего заданное полное ко­личество тепла. Действительно, граничное условие — к Jf~ ^{= o}(0

при * = 0 физически означает, что через каждую единицу пло­щади плоскости х = О мгновенно подводится количество тепла,

Дата добавления: 2014-11-07