Ol — V2X 54 страница

При заданном начальном термодинамическом состоянии газа (т. е. заданных р\, V\) ударная волна определяется всего одним каким-либо параметром: если, например, задать давление р₂ за волной, то по адиабате Гюгонио определится V₂, а затем по формулам (85,4) и (85,6) — плотность потока / и скорости vi и Vi. Напомним, однако, что мы рассматриваем здесь ударную волну в системе координат, в которой газ движется нормально к ее поверхности. Если же учесть возможность расположения ударной волны под косым углом к направлению потока, то по­надобится еще один параметр, например, значение касатель­ной к ее поверхности составляющей скорости.

Укажем здесь на следующее удобное графическое истолко­вание формулы (85,6). Если соединить хордой точку р_и Vi на ударной адиабате (рис. 53) с некоторой произвольной точкой р₂, V₂ на ней, то (р₂ — Pi) / (V₂— Vi)= —j² есть не что иное, как тангенс угла наклона этой хорды к оси абсцисс (к ее положи­тельному направлению). Таким образом, значение /, а с ним и скорости ударной волны, определяется в каждой точке ударной адиабаты углом наклона хорды, проведенной в эту точку из на­чальной точки.

Наряду с другими термодинамическими величинами в удар­ной волне испытывает разрыв также и энтропия. В силу закона возрастания энтропии последняя для газа может лишь возра­стать при его движении. Поэтому энтропия s₂ газа, прошедшего через ударную волну, должна быть больше его начальной энтро­пии Sb

s₂>si. (85,11)

Мы увидим ниже, что это условие налагает существенные огра­ничения на характер изменения всех величин в ударной волне.

Подчеркнем здесь следующее обстоятельство. Наличие удар­ных волн приводит к возрастанию энтропии при таких движе­ниях, которые можно рассматривать во всем пространстве как движение идеальной жидкости, не обладающей вязкостью и теп­лопроводностью. Возрастание энтропии означает необратимость движения, т. е. наличие диссипации энергии. Таким образом, разрывы представляют собой механизм, который приводит к диссипации энергии при движении идеальной жидкости. В связи с этим для движения тел в идеальной жидкости, сопровождаю­щегося возникновением ударных волн, не имеет места парадокс Даламбера (§ 11) — при таком движении тело испытывает силу сопротивления.

Разумеется, истинный механизм возрастания энтропии в ударных волнах заключен в диссипативных процессах, происхо­дящих в тех весьма тонких слоях вещества, которые в действи­тельности представляют собой физические ударные волны (см. § 93). Замечательно, однако, что величина этой диссипации це­ликом определяется одними лишь законами сохранения массы, энергии и импульса, примененными к обеим сторонам этих слоев: их ширина устанавливается как раз такой, чтобы дать требуе­мое этими законами сохранения увеличение энтропии.

Возрастание энтропии в ударной волне оказывает еще и дру­гое существенное влияние на движение: если движение газа впе­реди ударной волны потенциально, то за ней оно, вообще говоря, становится вихревым; мы вернемся к этому обстоятельству в § П4.

§ 86. Ударные волны слабой интенсивности

Рассмотрим ударную волну, в которой все величины испыты­вают лишь небольшой скачок; о таких разрывах мы будем гово­рить как об ударных волнах слабой интенсивности. Преобразуем соотношение (85,9), производя в нем разложение по степеням малых разностей s₂— Si и р₂ —Рь Мы увидим, что при таком разложении в (85,9) сокращаются члены первого и второго по­рядков по р₂— pi\ поэтому необходимо производить разложение по р₂ — р\ до членов третьего порядка включительно. По раз­ности же s₂— s\ достаточно разложить до членов первого по­рядка. Имеем:

= (|^)_р (* - s_t) + (|^-)_s (р₂ - р.) +

Но согласно термодинамическому соотношению dw — Tds -f* + Vdp имеем для производных:

(*).-'• (■£).-"•

Поэтому

Щ — Щ = 7", (s₂ — si) + Vi (р₂ — Pi) +

Объем У2 достаточно разложить только по р₂ — рь поскольку во втором члене уравнения (85,9) уже имеется малая разность •р₂ — pi и разложение по s₂—si дало бы член порядка (s₂ — — Si) (Р2 — Pi), не интересующий нас. Таким образом,

"•-"-(£).<* "'■>⁺т(3).⁽*-''-

Подставляя эти разложения в (85,9), получим следующее соот­ношение:

s₂-s, = -!— (~\ (p₂-pi)³. ⁽86,1)

Таким образом, скачок энтропии в ударной волне слабой интен­сивности является малой величиной третьего порядка по срав­нению со скачком давления.

Адиабатическая сжимаемость вещества — (дV/dp)_s практи­чески всегда падает с увеличением давления, т. е. вторая произ-

водная ')

(!?■). >°- ^

Подчеркнем, однако, что это неравенство не является термоди­намическим соотношением и, в принципе, возможны его нару­шения²). Как мы неоднократно увидим ниже, в газодинамике знак производной (86,2) весьма существен; в дальнейшем мы будем всегда считать его положительным.

Проведем через точку / (р_ь Vi) на р, К-диаграмме две кри­вые— ударную адиабату и адиабату Пуассона. Уравнение адиа­баты Пуассона есть s₂ — Si = 0. Из сравнения этого уравнения с уравнением (86,1) ударной адиабаты вблизи точки / видно, что обе кривые касаются в этой точке, причем имеет место каса­ние второго порядка — совпадают не только первые, но и вторые производные. Для того чтобы выяснить взаимное расположение обеих кривых вблизи точки /, воспользуемся тем, что согласно (86,1) и (86,2) при р2> Р\ на ударной адиабате должно быть Sa > si, между тем как на адиабате Пуассона остается s₂ = si-Поэтому абсцисса точки на ударной адиабате должна быть при той же ординате р₂ больше абсциссы точки на адиабате Пуас­сона. Это следует из того, что согласно известной термодинами­ческой формуле

V ds)р с_р \ дТ)_р

') Для политропного газа (д⁷У\ _ у+1 V_ \ dp²)s Y² Р² * Это выражение проще всего можно получить путем дифференцирования урав­нения адиабаты Пуассона pV^v = const. ^г) Так, это может иметь место в области вблизи критической точки жид­кость — газ. Ситуация с нарушением условия (86,2) может быть также имитирована на ударной адиабате для среды, допускающей фазовый переход (в результате чего на адиабате возникает излом). См. об этом в книге: Зель­дович Я- Б., Райзер Ю. П. Физика ударных волн и высокотемпературных гидродинамических явлений. — Изд. 2-е. — М.: Наука, 1966, гл. I, § 19; гл. XI, § 20. ⁸) При (dVldT)p < 0 расположение обеих кривых было бы обратным»

энтропия растет с увеличением объема при постоянном давле­нии — для всех тел, которые расширяются при нагревании, т. е. у которых (дУ/дТ)_р>0. Аналогично убеждаемся в том, что ниже точки / (т. е. при рй < pi) абсциссы точек адиабаты Пуассона должны быть больше абсцисс ударной адиабаты. Таким обра­зом, вблизи точки своего касания обе кривые расположены ука­занным на рис. 55 образом (##' — ударная адиабата, а РР' —• адиабаты Пуассона)³), причем в силу (86,2) обе обращены вог­нутостью вверх.

При малых р2—pi и V₂—Vi формулу (85,6) можно напи­сать в первом приближении в виде

г—т.

(мы пишем здесь производную при постоянной энтропии, имея в виду, что касательные к адиабатам Пуассона и ударной в точке 1 совпадают). Далее, скорости vi и v₂ в том же приближении одинаковы и равны

-я'-л/-^(*).-л/Ш.

Но это есть не что иное, как скорость зву­ка с. Таким образом, скорость распростра­нения ударных волн слабой интенсивности совпадает в первом приближении со ско­ростью звука:

v = c. (86,3)

Рис. 56 Из полученных свойств ударной адиаба-

ты в окрестности точки 1 можно вывести ряд существенных следствий. Поскольку в ударной волне долж­но выполняться условие s₂ > s\, то должно быть и

Р2 > Pl,

т. е. точки 2 (р₂, V₂) должны находиться выше точки /. Далее, поскольку хорда 12 идет круче касательной к адиабате в точке / (рис. 53), а тангенс угла наклона этой касательной равен про­изводной {dpi/dV\)si, имеем:

г->-Ш,-

Умножая это неравенство с обеих сторон на V\, находим:

где Ci — скорость звука, соответствующая точке /. Таким обра­зом,

Vi > С\.

Наконец, из того, что хорда 12 расположена менее круто, чем касательная в точке 2, аналогичным образом следует, что

V2 < С₂ ').

') Последняя аргументация применима только вблизи точки 1, где тан­генс угла наклона касательной к ударной адиабате в точке 2 отличается от производной {dp₂idVi)_s лишь на величину второго порядка малости.

§ 87] НАПРАВЛЕНИЕ ИЗМЕНЕНИЯ ВЕЛИЧИН В УДАРНОЙ ВОЛНЕ 463

Упомянем еще, в заключение, что при (d²V/dp²)_s <. О из ус­ловия S2 > Si для ударных волн слабой интенсивности следо­вало бы р₂ < Рь а для скоростей — те же неравенства v\ > С\, о₂ < с₂.

§ 87. Направление изменения величин в ударной волне

Таким образом, в предположении положительности производ­ной (86,2) для ударных волн слабой интенсивности можно весь­ма просто показать, что условие возрастания энтропии с необ­ходимостью приводит также и к неравенствам

р₂ > Рь (87,1)

oi > с_и v₂ < с₂. (87,2)

Из замечания, сделанного по поводу формулы (85,6) следует, что если р2 > Рь то

V₂ < V_u (87,3)

а поскольку / == V\/V\ = v₂/V₂, то и')

v_x > о₂. (87,4)

Неравенства (87,1) и (87,3) означают, что при прохождении газа через ударную волну происходит его сжатие — его давление и плотность возрастают. Неравенство oi > С\ означает, что ударная волна движется относительно находящегося перед ней газа со сверхзвуковой скоростью; ясно поэтому, что в этот газ не могут проникнуть никакие исходящие от ударной волны воз­мущения. Другими словами, наличие ударной волны вовсе не сказывается на состоянии газа впереди нее.

Покажем теперь, что все неравенства (87,1—4) справедливы и для ударных волн произвольной интенсивности — при том же предположении о знаке производной (d²V/dp²)_s²).

') Если перейти в систему отсчета, в которой газ / перед ударной вол­ной покоится, а волна движется, то неравенство t>i > i/₂ означает, что газ позади ударной волны будет двигаться (со скоростью v_x — i>₂) в ту же сто­рону, куда движется сама волна. ²) Неравенства (87,1—4) были получены для ударных волн произвольной интенсивности в политропном газе Жуге (£. Jouguet, 1904) н Цемпленом (G, Zemplen, 1905). Излагаемое ниже доказательство для произвольной среды дано Л. Д. Ландау (1944).

Величина j² определяет наклон хорды, проведенной из на­чальной точки ударной адиабаты / в произвольную точку 2 (—j² есть тангенс угла наклона этой хорды к оси V). Пока­жем, прежде всего, что направление изменения этой величины при перемещении точки 2 вдоль адиабаты однозначно связано с направлением изменения энтропии s₂ при том же переме­щении.

Продифференцируем соотношения (85,5) и (85,8) по вели­чинам, относящимся к газу 2 при заданном состоянии газа /. Это значит, что дифференцируются р₂> V₂, w₂ и / при задан­ных значениях р_ь V\, w\. Из (85,5) получаем:

dp₂ + j² dV₂ = {V\ - V₂) d (j²), (87,5)

а из (85,8):

dw₂ + j²V₂ dV₂ = \ (V² - Vl) d {f) или, раскрыв дифференциал dw₂:

т₂ ds₂ + v₂ {d_P2 + f dv₂)=j {v] - vi) d (/).

Подставив сюда dp₂ + j²dV₂ из (87,5), получим соотношение

T₂ds₂ = ±{V_x-V₂)²d(f).

(87,6)

Отсюда видно, что

d(j²)/ds₂>0,

(87,7)

т. е. j² и s₂ меняются в одинаковом направлении.

Дальнейшие рассуждения имеют своей следующей целью по­казать, что на ударной адиабате не может быть точек, в кото­рых бы она касалась проведенной из точки / прямой (как это имело бы место в точке О на рис. 56.

В такой точке угол наклона хорды (прове­денной из точки /) имеет минимум, а /²—со­ответственно максимум, и потому

d(j²)/dp₂ = 0.

Рис. 56

_ Из соотношения (87,6) видно, что в таком V случае будет и

ds₂/dp₂ = 0.

Далее, вычислим производную d(j²)/dp₂ в произвольной точ­ке ударной адиабаты. Подставив в соотношение (87,5) диффе­ренциал dV₂ в виде

взяв для ds₂ выражение (87,6) и разделив все равенство на dp₂, получим

dpi

(V, - V₂) [l­

2Г_а

j² (У, - У_г) (dVi

\ ds₂ /pj

(87,8)

Отсюда видно, что обращение этой производной в нуль влечет за собой также и равенство

6V, - -²

V 3Pi Js, ^с2

т. е. U2 = с₂. Обратно, из равенства у₂ = с₂ следует, что произ­водная d(j²)/dp₂ = 0; последняя могла бы не обратиться в нуль, лишь если бы вместе с числителем в (87,8) обратился бы в нуль также и знаменатель; но выражения в числителе и знаме­нателе представляют собой две различные функции точки 2 на ударной адиабате, их одновременное обращение в нуль могло бы произойти лишь чисто случайно и потому невероятно¹). Таким образом, все три равенства

чрт=*> ж-⁰' ^v*=^c* <⁸⁷-⁹>

являются следствиями друг друга и имели бы место одновре­менно в точке О на кривой рис. 56 (имея в виду последнее из этих равенств, будем условно называть такую точку звуковой). Наконец, для производной от (v₂/c₂)² в этой точке имеем

dp₂\4) d_P.₂['\др₂л,J Vдр²₂А/

Ввиду предполагаемой везде положительности производной (d²V/dp²)_s имеем, следовательно, в звуковой точке:

Тр-Л<*- <⁸⁷'¹⁰>

Теперь уже легко доказать невозможность существования звуковой точки на ударной адиабате. В точках, лежащих вблизи начальной точки / над ней, имеем и₂ < с₂ (см. конец предыду­щего параграфа). Поэтому равенство v₂ = с₂ может быть до­стигнуто лишь при увеличении у₂/с₂; другими словами, в звуко­вой точке должно было бы быть d(vi/c₂) /dp₂ > 0, между тем как согласно (87,10) мы имеем как раз обратное неравенство. Аналогичным образом можно убедиться в невозможности обра­щения v₂/c₂ в единицу и на нижней части ударной адиабаты, под точкой /.

Имея в виду доказанную таким образом невозможность су­ществования звуковых точек, можно заключить непосредственно из графика ударной адиабаты, что угол наклона хорды 12 умень­шается при передвижении точки 2 вверх по кривой, а /² соот-

') Подчеркнем, во избежание недоразумений, что сама производная d('f)Idp2 не является еще одной независимой функцией точки 2; выражение (87,8) есть ее определение.

ветственно монотонно возрастает; ввиду неравенства (87,7) от­сюда следует, что монотонно возрастает и энтропия s₂. Таким образом, при соблюдении необходимого условия s₂ > Sj будет и р₂ > Рь

Легко, далее, убедиться в том, что на верхней части удар­ной адиабаты справедливы также и неравенства v₂ < с_2> v\ > С\. Первое следует прямо из того, что оно справедливо вблизи точки /, а сделаться равным единице отношение v₂/c₂ нигде не может. Второе следует из того, что ввиду невозмож­ности такого перегиба адиабаты, какой изображен на рис. 56, всякая хорда из точки / в находящуюся над ней точку 2 рас­положена более круто, чем касательная к ударной адиабате в точке /.

Таким образом, на верхней части ударной адиабаты выпол­няются условие s₂ > s\ и все три неравенства (87,1—2). Наобо­рот, на нижней части адиабаты все эти условия не выполняют­ся. Следовательно, все эти условия оказываются эквивалент­ными друг другу и выполнение одного из них автоматически влечет за собой также и выполнение всех остальных.

Напомним лишний раз, что в изложенных рассуждениях все время предполагалось выполненным условие положительности производной (d²V/dp²)_s. Если эта производная могла бы ме­нять знак, то из необходимого термодинамического неравенства s₂ > Si уже нельзя было бы сделать никаких универсальных за­ключений о неравенствах для остальных величин.

§ 88. Эволюционность ударных волн

Вывод неравенств (87,1—4) в §§ 86, 87 был связан с определенным предположением о термодинамических свойствах среды —с положительностью производной (d²V/dp²)_s. Весьма существенно, однако, что неравенства

vi > си v₂ < с₂ (88,1)

для скоростей могут быть получены также и из совершенно иных соображений, показывающих, что ударные волны с нару­шенными условиями (88,1) все равно не могли бы существо­вать, даже если бы это не противоречило изложенным выше чисто термодинамическим соображениям ').

') Напомним в то же время, что (по крайней мере для ударных волн слабой интенсивности) эти термодинамические соображения приводят к усло­виям (88,1) также и при (д² V/др²) _s < 0, когда ударная волна является вол­ной разрежения (а не сжатия); это обстоятельство было отмечено в конце § 86.

Именно необходимо исследовать еще вопрос об устойчивости ударных волн. Наиболее общее необходимое условие устойчи­вости состоит в требовании, чтобы любое бесконечно малое воз-

мущение начального (в некоторый момент t — 0) состояния при-
водило бы лишь к вполне определенным бесконечно малым же
изменениям течения, — по крайней мере в течение достаточно
малого промежутка времени t. Последняя оговорка означает не-
достаточность указанного условия; так, если начальное малое
возмущение возрастает даже экспоненциально (как с поло-
жительной постоянной у), то в течение времени t возму-
щение остается малым, хотя в конце концов оно и приводит к
разрушению данного режима движения. Возмущением, не удов-
летворяющим поставленному необходимому условию, является
расщепление ударной волны на два (или более) последователь-
ных разрыва; очевидно, что изменение движения при этом сразу
же оказывается не малым, хотя при малых t (когда оба раз-
рыва не разошлись еще на большое расстояние) оно и занимает
лишь небольшой интервал расстояний ох.

Произвольное начальное малое возмущение определяется не­которым числом независимых параметров. Дальнейшая же эво­люция возмущения определяется системой линеаризованных гра­ничных условий, которые должны удовлетворяться на поверх­ности разрыва. Поставленное выше необходимое условие устой­чивости будет выполнено, если число этих уравнений совпадает с числом содержащихся в них неизвестных параметров — тогда граничные условия определяют дальнейшее развитие возмуще­ния, которое при малых t > 0 останется малым. Если же число уравнений больше или меньше числа независимых параметров, то задача о малом возмущении не имеет решений вовсе или имеет их бесконечное множество. Оба случая свидетельствовали бы о неправомерности исходного предположения (малость воз­мущения при малых г) и, таким образом, противоречили бы по­ставленному требованию. Сформулированное таким образом условие называют условием эволюционности течения.

¹) Излагаемое ниже обоснование неравенств (88,1) принадлежит Л. Д. Ландау (1944).

Рассмотрим возмущение ударной волны, представляющее со­бой ее бесконечно малое смещение в направлении, перпендику­лярном ее плоскости¹). Оно сопровождается бесконечно малым возмущением также и других величин — давления, скорости и т. д. газа по обеим сторонам поверхности разрыва. Эти воз­мущения, возникнув вблизи волны, будут затем распространять­ся от нее, переносясь (относительно газа) со скоростью звука; это не относится лишь к возмущению энтропии, которое будет переноситься только с самим газом. Таким образом, произволь­ное возмущение данного типа можно рассматривать как сово­купность звуковых возмущений, распространяющихся в газах / и 2 по обе стороны ударной волны, и возмущения энтропии; по­следнее, перемещаясь вместе с газом, будет, очевидно, существо­вать лишь в газе 2 позади ударной волны. В каждом из звуко­вых возмущений изменения всех величин связаны друг с другом определенными соотношениями, следующими из уравнений дви­жения (как в любой звуковой волне; § 64); поэтому каждое та­кое возмущение определяется всего лишь одним параметром.

Подсчитаем теперь число возможных звуковых возмущений. Оно зависит от относительной величины скоростей газа v\, v₂ и скоростей звука С\, с₂. Выберем направление движения газа (со стороны / на сторону 2) в качестве положительного направления оси х. Скорость распространения возмущения в газе / относи­тельно неподвижной ударной волны есть u\—V\±C\, а в газе 2 «2 = v2 ± с₂. Тот факт, что эти возмущения должны распростра­няться по направлению от ударной волны, означает, что должно быть «] < 0, и₂ > 0.

v,>c.	vz<c2	vt<c,	V2<EZ
		—-
©		©
	vz>cz	ц<с,	vz>c2
	X	©

Предположим, что v\ > с_и о₂ < с₂. Тогда ясно, что оба зна­чения щ = v\ ± с\ будут положительными, а из двух значений

м₂ будут положительными лишь v₂ + -f с₂. Это значит, что в газе / вообще не сможет быть интересующих нас звуковых возмущений, а в газе 2 — всего одно, распространяющееся отно­сительно самого газа со скоростью -}- с₂. Аналогичным образом произво­дится подсчёт в других случаях.

Результат изображен на рис. 57,
где каждая стрелка соответствует од-
ному звуковому возмущению, распро-
Рис. 57 страняющемуся относительно газа в

указываемую стрелкой сторону. Каж­дое же звуковое возмущение определяется, как было выше ука­зано, одним параметром. Кроме того, во всех четырех случаях имеется еще по два параметра: параметр, определяющий рас­пространяющееся в газе 2 возмущение энтропии, и параметр, определяющий самое смещение ударной волны.

Для каждого из четырех случаев на рис. 57 цифрой в круж­ке указано получающееся таким образом полное число парамет­ров, определяющих произвольное возмущение, возникающее при смещении ударной волны.

С другой стороны, число необходимых граничных условий, ко­торым должно удовлетворять возмущение на поверхности раз­рыва, равно трем (условия непрерывности потоков массы, энер­гии и импульса). Во всех изображенных на рис. 57 случаях, за исключением лишь первого, число имеющихся независимых па­раметров превышает число уравнений. Мы видим, что эволю-ционны лишь ударные волны, удовлетворяющие условиям (88,1). Эти условия, таким образом, необходимы для существования ударных волн, вне зависимости от термодинамических свойств

среды. Искусственно созданный разрыв, не удовлетворяющий этим условиям, немедленно распался бы на другие разрывы¹).

Эволюционная ударная волна устойчива по отношению к рассмотренному типу возмущений и в обычном смысле этого сло­ва. Если искать смещение ударной волны (а с ним и возмуще­ния всех остальных величин) в виде, пропорциональном е~^ш, то заранее очевидно, что однозначно определяемое граничными условиями значение со может быть только нулем — уже хотя бы из тех соображений, что в задаче нет никаких параметров раз­мерности обратного времени, которые могли бы определить от­личное от нуля значение со.

Мы вернемся к вопросу об устойчивости ударных волн в § 90.

§ 89. Ударные волны в политропном газе

Применим полученные в предыдущих параграфах общие со­отношения к ударным волнам в политропном газе.

Тепловая функция такого газа дается простой формулой
(83,11). Подставив это выражение в (85,9), получим после про-
стого преобразования р₂/р₁
следующую формулу: i

Ll-v_t —

^_ (у+ 1) pi + (у — 1>ра (Y-l)Pi + (Y+»)/»» " (89,1)

О -1/6

Рис. 58

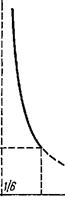
По этой формуле можно определить по трем из величин р_и Vi, р₂, V₂ чет­вертую. Отношение V₂/V\ является монотонно убы­вающей функцией отно­шения pi/pi, стремящей­ся к конечному пределу (у—1)/(у+1). Кривая, изображающая зависи­мость между р₂ и V₂ при заданных р\, V\ (ударная адиабата), представлена на рис. 58. Это — равнобочная гипербола с асимптотами

Y+ 1

Уг у — 1 £± Y—1

Pi

Y+ 1

') Во всех перечисленных на рис. 57 неэволюционных случаях возмуще­ние недоопределено — число произвольных параметров превышает число урав­нений Упомянем, что в магнитной гидродинамике ударные волны могут быть неэволюционными в силу кзк недоопределенности, так и переопределенности возмущений (см. VIII, § 73).

Реальным смыслом обладает, как мы знаем, только верхняя часть кривой над точкой V₂/Vi = Р2/Р1 = 1, изображенная на рис. 58 (для у = 1,4) сплошной линией.

Для отношения температур с обеих сторон разрыва имеем согласно уравнению состояния термодинамически идеального газа Т₂/Т_х = p₂V₂/piVi, так что

ll — H. Г <У + ^!>Р' + (V —0Р2 1 /oq ™

Ti р, L(Y-1)P. + (Y+1)P₂J^{- (} '>

Для потока / получаем из (85,6) и (89,1):

;2 _ (Y — 0 Pi + (у+ О Р2 _(яа о\

/------------------- 21Л----------- (оУ.-э)

и отсюда для скорости распространения ударной волны относи­тельно газов впереди и позади нее:

.2

°i = Т" [(V - 1) Pi + (Y + 1) Р₂] -= |г [(V ~ D + (Y + 1).

(89 4)

„ У, [(У+1)Р! + (У-1)Р₂]² с₂ Г, п. /,п^р<1 ^pl°-2-[(Y-l)p, + (Y+l)p₂l ⁼2^L<V-D + (Y+1)-^J.

и для разности скоростей:

V2TT(p₂-p,) ₅₎

[(Y-l)Pi + (Y+Dp₂]^{,/2 V}

В применениях полезны формулы, выражающие отношения плотностей, давлений и температур в ударной волне через число Mi = Vi/cu эти формулы без труда выводятся из полученных выше соотношений и гласят:

^Р2 " ^{(Y + 1)M}' (89,6)

р, о₂ (_v_l)Mf + 2

_Pl ^. - V*,- (ад

£2_ Pl

Г₂ [_2YM²-(v-l)][(Y-l)M² + 2]

Г, (y + 0²М² ' ¹ ' '

Число же М₂ = у₂/с₂ выражается через число Mi посредством

₂ 2 + (у-1)М²

М? = —-5^ —. (89,9)

2_YM²-(y- 1) ^v

Это соотношение симметрично относительно Mi и М₂, как это •становится очевидным, если записать его в виде уравнения

2yMiMl - (y — 1) (М? + Ml) = 2.

Выпишем предельные формулы для ударных волн очень большой интенсивности (требуется, чтобы бьмо (7 — 1)р₂"> >(V— 1)pi). Имеем из (89,1—2):

Дата добавления: 2014-11-07