
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Статистическая проверка статистических гипотез
|
|
|
|
Статистической называют гипотезу о виде неизвестного распределения или о параметре известного распределения.
Наряду с выдвинутой гипотезой рассматривают и противоречащую ей гипотезу. Если выдвинутая гипотеза будет отвергнута, то имеет место противоречащая гипотеза.
Нулевой (основной) называют выдвинутую гипотезу Н 0.
Конкурирующей (альтернативной) называют гипотезу Н 1, которая противоречит нулевой.
Например, если нулевая гипотеза состоит в предположении, что математическое ожидание а нормального распределения равно 10 (Н 0: а = 10), то конкурирующая гипотеза, в частности, может состоять в предположении, что а ≠ 10 (Н 1: а ≠ 10).
Простой называют гипотезу, содержащую только одно предположение.
Сложной называют гипотезу, которая состоит из конечного или бесконечного числа простых гипотез.
Так как проверку статистической гипотезы проводят статистическими методами, то ее (проверку) называют статистической.
В итоге проверки в двух случаях может быть принято неправильное решение, т.е. могут быть допущены ошибки двух родов.
Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза.
Ошибка второго рода состоит в том, что будет принята неправильная гипотеза.
Вероятность совершить ошибку первого рода обозначают через  и называют уровнем значимости.
и называют уровнем значимости.
Чаще всего берут  =0,05 или
=0,05 или  =0,01. Если, например, взять уровень значимости
=0,01. Если, например, взять уровень значимости  = 0,05, то это означает, что в пяти случаях из ста имеется риск допустить ошибку первого рода.
= 0,05, то это означает, что в пяти случаях из ста имеется риск допустить ошибку первого рода.
Статистическим критерием (критерием) называют случайную величину К, которая служит для проверки нулевой гипотезы Н 0.
Наблюдаемым значением Кнабл. называют значение критерия, вычисленное по выборкам.
|
|
|
Критической областью называют совокупность значений критерия, при которых Н 0 отвергают.
Областью принятия гипотезы (областью допустимых значений) называют совокупность значений критерия, при которых гипотезу принимают.
Основной принцип проверки статистических гипотез: если наблюдаемое значение критерия принадлежит критической области, то гипотезу отвергают; если наблюдаемое значение критерия принадлежит области принятия гипотезы, то гипотезу принимают.
Критическими точками (границами) Ккр называют точки, отделяющие критическую область от области принятия гипотезы.
Правосторонней называют критическую область, определяемую неравенством К > Ккр, где Ккр – положительное число

Левосторонней называют критическую область, определяемую неравенством К < Ккр, где Ккр – отрицательное число
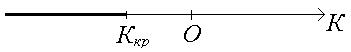
Односторонней называют правостороннюю или левостороннюю критическую область.
Двусторонней называют критическую область, определяемую неравенствами К < Ккр .1, К > Ккр .2, где Ккр .2 > Ккр .1

В частности, если критические точки симметричны относительно нуля, то двусторонняя критическая область определяется неравенствами (в предположении, что Ккр > 0)
К <− Ккр, К > Ккр,
или
| К | > Ккр

При нахождении критической области задаются уровнем значимости  и ищут критические точки, исходя из следующих соотношений:
и ищут критические точки, исходя из следующих соотношений:
а) для правосторонней критической области
Р (К > Ккр) =  (Ккр > 0);
(Ккр > 0);
б) для левосторонней критической области
Р (К < Ккр) =  (Ккр < 0);
(Ккр < 0);
в) для двусторонней симметричной области
Р (К > Ккр) = 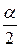 , Р (К <− Ккр) =
, Р (К <− Ккр) = 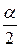
(Ккр > 0).
Мы строили критическую область, исходя из требования, чтобы вероятность попадания в нее критерия была равна  при условии, что справедлива нулевая гипотеза. Оказывается целесообразным ввести в рассмотрение вероятность попадания критерия в критическую область при условии, что нулевая гипотеза неверна и, следовательно, справедлива конкурирующая гипотеза.
при условии, что справедлива нулевая гипотеза. Оказывается целесообразным ввести в рассмотрение вероятность попадания критерия в критическую область при условии, что нулевая гипотеза неверна и, следовательно, справедлива конкурирующая гипотеза.
|
|
|
Мощностью критерия называют вероятность попадания критерия в критическую область при условии, что справедлива конкурирующая гипотеза.
Другими словами, мощность критерия есть вероятность того, что нулевая гипотеза будет отвергнута, если верна конкурирующая гипотеза.
В этом случае строят критическую область так, чтобы мощность критерия была максимальной. Если вероятность ошибки второго рода (принять неправильную гипотезу) равна  , то мощность равна 1−
, то мощность равна 1− . Если мощность 1−
. Если мощность 1− возрастает, то уменьшается вероятность
возрастает, то уменьшается вероятность  совершить ошибку второго рода. Таким образом, чем мощность больше, тем вероятность ошибки второго рода меньше.
совершить ошибку второго рода. Таким образом, чем мощность больше, тем вероятность ошибки второго рода меньше.
Замечание. Уменьшить одновременно  и
и  невозможно: если уменьшить
невозможно: если уменьшить  , то
, то  будет возрастать.
будет возрастать.
Единственный способ одновременного уменьшения вероятностей ошибок первого и второго рода состоит в увеличении объема выборок.
Проверка гипотезы о согласованности мнений экспертов (априорное ранжирование переменных)
Пусть т специалистам (экспертам), хорошо знакомым с исследуемым процессом, предлагается расположить п факторов Х 1, Х 2, …, Хп в порядке убывания их влияния на результат процесса (на переменную состояния Y).
Пусть аij – ранг, выставленный i -м экспертом j -му фактору (1 ≤ аij ≤ п, i = 1, 2, …, m, j = 1, 2, …, n).
Результаты опроса вносятся в таблицу
| Факторы Эксперты | Х 1 | Х 2 | … | Хп |
| а 11 | а 12 | … | а 1 п | |
| а 21 | а 22 | … | а 2 п | |
| … | … | … | … | … |
| т | ат 1 | ат 2 | … | атп |
По результатам опроса экспертов проверяется гипотеза
Н 0: мнения экспертов согласованы
при конкурирующей гипотезе
Н 1: мнения экспертов не согласованы (рассогласованы).
Сумма рангов по строке (сумма рангов, выставляемых конкретным экспертом) для всех строк одинакова и равна
 .
.
Среднее значение рангов в строке:
 .
.
Среднее значение суммы рангов в столбце:
 .
.
Вычисляется коэффициент согласия (коэффициент конкордации):
W = 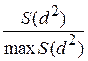 ,
,
где S (d 2) – сумма квадратов отклонения суммы рангов от средней суммы:
S (d 2) =  =
=  ,
,
 =
= 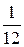 т 2(п 3 − п).
т 2(п 3 − п).
Если мнения экспертов согласованы, то S (d 2) =  , т.е. W = 1.
, т.е. W = 1.
Если мнения экспертов не согласованы, то значение S (d 2) близко к нулю и W ≈ 0.
|
|
|
Если из нескольких факторов эксперт ни одному не может отдать предпочтение, то в этом случае в таблицу ранжирования этим факторам он выставляет одинаковые дробные ранги. Тогда коэффициент конкордации вычисляется по формуле
W =  =
=  ,
,
где
Ti = 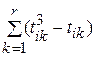 ,
,
где i – номер эксперта;
k – номер повторения;
tik – число одинаковых рангов в k- ом повторении у i -го эксперта.
Для проверки нулевой гипотезы Н 0 в качестве статистического критерия используют случайную величину
 = (п − 1) тW,
= (п − 1) тW,
т.е. используют  -распределение с числом степеней свободы k = n − 1. При этом строится левосторонняя критическая область.
-распределение с числом степеней свободы k = n − 1. При этом строится левосторонняя критическая область.
Правило проверки гипотезы Н 0
1. Вычисляют наблюдаемое значение критерия
 = (п − 1) тW.
= (п − 1) тW.
2. По заданному уровню значимости  и числу степеней свободы k = n − 1 определяют критическую точку
и числу степеней свободы k = n − 1 определяют критическую точку 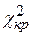 (
( ; k) по таблице критических точек
; k) по таблице критических точек  -распределения.
-распределения.
3. Если  >
> 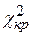 , то гипотеза Н 0 принимается, т.е. мнения экспертов согласуются;
, то гипотеза Н 0 принимается, т.е. мнения экспертов согласуются;
Если  <
< 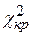 , то мнения экспертов рассогласованы.
, то мнения экспертов рассогласованы.
Если мнения экспертов согласованы, то строится ранжировочная гистограмма. В ней по оси абсцисс откладываются факторы, а по оси ординат – суммы рангов в обратном порядке.
По виду гистограммы судят о значимом или незначимом влиянии факторов на переменную состояния и об использовании этих факторов в дальнейшем.
Пример. Для некоторого технологического объекта рассматриваются 6 факторов, влияющих на переменную состояния. Мнения 4 экспертов приведены в таблице
| Факторы Эксперты | Х 1 | Х 2 | Х 3 | Х 4 | Х 5 | Х 6 |
| 1,5 | 1,5 | |||||
| 4,5 | 4,5 | |||||
| 5,5 | 5,5 |
Проверить гипотезу о согласованности мнений экспертов и, если они справедливы, то построить гистограмму ранжирования. Уровень значимости взять равным  = 0,05.
= 0,05.
□
Имеем п = 6, т = 4. Найдем среднее значение суммы рангов в столбце:
 =
=  = 14.
= 14.
Построим таблицу
| Факт. Эксп. | Х 1 | Х 2 | Х 3 | Х 4 | Х 5 | Х 6 | ti 1 |
 - ti 1 - ti 1
| ti 2 |
 - ti 2 - ti 2
| Ti |
| 1,5 | 1,5 | ||||||||||
| 4,5 | 4,5 | ||||||||||
| 5,5 | 5,5 | ||||||||||
| 4 | 1,5 | 3,5 | 1,5 | 3,5 | |||||||

| 14,5 | 16,5 | |||||||||
| dj | −7 | 0,5 | −9 | 2,5 | |||||||

| 0,25 | 6,25 |
|
|
|
Так как в таблице присутствуют дробные ранги, то коэффициент кокордации вычисляем по формуле
W =  .
.
Найдем S (d 2):
S (d 2) =  =
=  =
=  = 49+0,25+81+25+6,25+64 = 225,5.
= 49+0,25+81+25+6,25+64 = 225,5.
Найдем 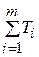 :
:
Ti = 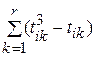 =
= 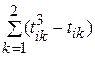 :
:
T 1 = (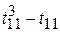 ) + (
) + (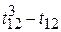 ) = 6 + 0 = 6,
) = 6 + 0 = 6,
T 2 = (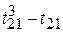 ) + (
) + (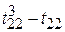 ) = 6 + 0 = 6,
) = 6 + 0 = 6,
T 3 = (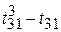 ) + (
) + (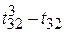 ) = 6 + 0 = 6,
) = 6 + 0 = 6,
T 4 = (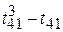 ) + (
) + ( ) = 6 + 6 = 12.
) = 6 + 6 = 12.
Тогда
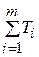 =
=  = 6 + 6 + 6 + 12 = 30.
= 6 + 6 + 6 + 12 = 30.
Следовательно,
W =  =
= 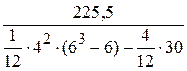 = 0,805.
= 0,805.
Проверка гипотезы Н 0:
1.Вычислим наблюдаемое значение критерия:
 =(п − 1) тW = 4·(6 – 1)·0,805=16,1.
=(п − 1) тW = 4·(6 – 1)·0,805=16,1.
2. По заданному уровню значимости  = 0,05 и числу степеней свободы k = 6 − 1 = 5 определим критическую точку
= 0,05 и числу степеней свободы k = 6 − 1 = 5 определим критическую точку 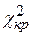 (
( ; k) по таблице критических точек
; k) по таблице критических точек  -распределения:
-распределения:
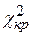 (
( ; k) =
; k) = 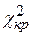 (0,05;5) = 11,07.
(0,05;5) = 11,07.
3. Так как  >
> 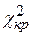 , то мнения экспертов согласованы (гипотеза Н 0 принимается).
, то мнения экспертов согласованы (гипотеза Н 0 принимается).
Построим ранжировочную гистограмму:

■
Проверка гипотезы о нормальном распределении генеральной совокупности по критерию Пирсона
Пусть имеется эмпирическое распределение в виде последовательности вариант. Требуется, используя критерий Пирсона, проверить гипотезу Н 0: генеральная совокупность Х распределена по нормальному закону.
Правило проверки гипотезы Н 0
1. Записать эмпирическое распределение в виде последовательности интервалов [ xi, xi +1) c соответствующими частотами пi (пi – сумма частот, попавших в i -й интервал):
[ xi, xi +1): [ x 1, x 2) [ x 2, x 3) …[ xs, xs +1)
пi: п 1 п 2 … пs
2. Вычислить выборочную среднюю 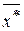 и среднее квадратическое отклонение
и среднее квадратическое отклонение 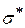 , причем в качестве варианты
, причем в качестве варианты 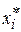 принимают среднее арифметическое концов интервала:
принимают среднее арифметическое концов интервала:
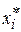 =
= 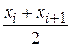 .
.
3. Пронормировать Х, т.е. перейти к случайной величине
Z =  ,
,
и вычислить концы интервалов:
zi =  , zi +1 =
, zi +1 =  ,
,
причем наименьшее значение Z, т.е. z 1, полагают равным −∞, а наибольшее, т.е. zs, полагают равным +∞.
4. Вычисляют теоретические частоты
 = п · Рi,
= п · Рi,
где
п – объем выборки;
Рi = Φ (zi +1) − Φ (zi) – вероятность попадания Z в интервалы (zi, zi +1), Φ (z) – функция Лапласа.
5. Сравнить эмпирические и теоретические частоты с помощью критерия Пирсона. Для этого:
а) составляют расчетную таблицу, по которой находят наблюдаемое значение критерия Пирсона
 =
= 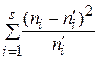 ;
;
б) по таблице критических точек распределения  , по заданному уровню значимости
, по заданному уровню значимости  и числу степеней свободы k = s – 3 (s – число интервалов выборки) находят критическую точку правосторонней критической области
и числу степеней свободы k = s – 3 (s – число интервалов выборки) находят критическую точку правосторонней критической области 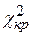 (
( , k).
, k).
6. Если  <
< 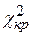 , то гипотезу Н 0 о нормальном распределении генеральной совокупности принимается. Другими словами, эмпирические и теоретические частоты различаются незначимо.
, то гипотезу Н 0 о нормальном распределении генеральной совокупности принимается. Другими словами, эмпирические и теоретические частоты различаются незначимо.
Если  >
> 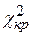 , то гипотезу Н 0 отвергают. Другими словами, эмпирические и теоретические частоты различаются значимо.
, то гипотезу Н 0 отвергают. Другими словами, эмпирические и теоретические частоты различаются значимо.
Пример. Используя критерий Пирсона, при уровне значимости  = 0,05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности Х с эмпирическим распределением выборки объема п = 100:
= 0,05 проверить, согласуется ли гипотеза о нормальном распределении генеральной совокупности Х с эмпирическим распределением выборки объема п = 100:
5, 10, 13, 15, 7, 20, 14, 12, 20, 20, 16, 20, 18, 18, 25, 27, 13, 5, 20, 20, 23, 20, 18, 14, 20, 20, 10, 12, 15, 7, 13, 28, 18, 15, 16, 20, 20, 18, 18, 13, 17, 12, 8, 7, 8, 7, 13, 8, 13, 20, 20, 20, 25, 23, 23, 28, 17, 18, 18, 20, 20, 20, 23, 25, 28, 30, 33, 37, 18, 25, 18, 18, 20, 20, 20, 25, 28, 23, 23, 20, 20, 23, 23, 30, 32, 35, 20, 20, 18, 18, 18, 20, 23, 23, 18, 32, 33, 35, 33, 33.
□
Запишем распределение выборки в виде
хi 5 7 8 10 12 13 14 15 16 17 18 20 23 25 27 28 30 32 33 35 37
ni 2 4 3 2 3 6 2 3 2 2 15 25 10 5 1 4 2 2 4 2 1
1. Запишем эмпирическое распределение в виде последовательности интервалов c соответствующими частотами. Пусть началом первого интервала будет 3, а шаг равен 5. Учитываем, что левая граница входит в интервал, а правая не входит:
Таблица 1.
| Номер интервала, i | Границы интервала | Частота, пi | |
| xi | xi +1 | ||
2. Вычислим выборочную среднюю 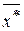 и среднее квадратическое отклонение
и среднее квадратическое отклонение 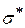 , причем в качестве варианты
, причем в качестве варианты 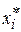 принимают среднее арифметическое концов интервала:
принимают среднее арифметическое концов интервала:
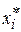 =
= 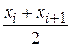 .
.
В результате получим распределение:
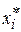 5,5 10,5 15,5 20,5 25,5 30,5 35,5
5,5 10,5 15,5 20,5 25,5 30,5 35,5
ni 6 8 15 40 16 8 7
Тогда
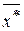 =
=  =
=  ·(6·5,5+8·10,5+15·15,5+40·20,5+16·25,5+8·30,5+7·35,5 = 20,7;
·(6·5,5+8·10,5+15·15,5+40·20,5+16·25,5+8·30,5+7·35,5 = 20,7;
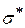 =
= 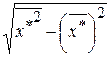 ;
;
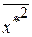 =
=  =
=  ·(6·5,52 +8·10,52 +15·15,52 +40·20,52 +16·25,52 +8·30,52 +7·35,52 =
·(6·5,52 +8·10,52 +15·15,52 +40·20,52 +16·25,52 +8·30,52 +7·35,52 =
= 481,45;
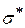 =
= 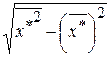 =
= 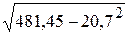 = 7,28.
= 7,28.
3. Найдем интервалы (zi, zi +1), учитывая, что 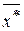 = 20,7 и
= 20,7 и 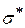 = 7,28. Для этого составим таблицу 2 (левый конец первого интервала примем равным −∞, а правый конец последнего интервала примем равным +∞)
= 7,28. Для этого составим таблицу 2 (левый конец первого интервала примем равным −∞, а правый конец последнего интервала примем равным +∞)
Таблица 2.
| i | Границы интервала | Границы интервала | ||
| хi | xi +1 | zi = 
| zi +1 = 
| |
| −∞ | −1,74 | |||
| −1,74 | −1,06 | |||
| −1,06 | −0,37 | |||
| −0,37 | 0,32 | |||
| 0,32 | 1,00 | |||
| 1,00 | 1,69 | |||
| 1,69 | +∞ |
4. Найдем теоретические вероятности Рi и теоретические частоты  = п · Рi. Для этого составим таблицу 3.
= п · Рi. Для этого составим таблицу 3.
Таблица 3.
| i | Границы интервала | Pi = = Φ (zi +1)− − Φ (zi) |  =
=100 Рi =
=100 Рi
| |
| zi | zi +1 | |||
| −∞ | −1,74 | 0,0409 | 4,09 | |
| −1,74 | −1,06 | 0,1037 | 10,37 | |
| −1,06 | −0,37 | 0,2111 | 21,11 | |
| −0,37 | 0,32 | 0,2698 | 26,98 | |
| 0,32 | 1,00 | 0,2158 | 21,58 | |
| 1,00 | 1,69 | 0,1132 | 11,32 | |
| 1,69 | +∞ | 0,0455 | 4,55 | |

|
5. Сравним эмпирические и теоретические частоты, используя критерий Пирсона:
а) вычислим наблюдаемое значение критерия Пирсона. Для этого составим расчетную таблицу 4.
Таблица 4.
| i | ni |

| 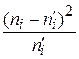
| 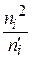
|
| 4,09 | 0,8920 | 8,8019 | ||
| 10,37 | 0,5416 | 6,1716 | ||
| 21,11 | 1,7684 | 10,6584 | ||
| 26,98 | 6,2833 | 59,3052 | ||
| 21,58 | 1,4428 | 11,8628 | ||
| 11,32 | 0,9737 | 5,6537 | ||
| 4,55 | 1,3192 | 10,7692 | ||

|  =13,22 =13,22
| 113,22 |
Последний столбец служит для котроля: разница 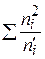 − п должна равняться наблюдаемому значению критерия Пирсона. Проверим это:
− п должна равняться наблюдаемому значению критерия Пирсона. Проверим это:
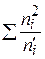 − п = 113,22 − 100 =13,22 =
− п = 113,22 − 100 =13,22 =  .
.
Значит, вычисления выполнены правильно.
б) по таблице критических точек распределения 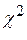 по уровню значимости
по уровню значимости  = 0,05 и числу степеней свободы k = s – 3 = 7 − 3 = 4 (s – число интервалов выборки) найдем критическую точку правосторонней критической области
= 0,05 и числу степеней свободы k = s – 3 = 7 − 3 = 4 (s – число интервалов выборки) найдем критическую точку правосторонней критической области 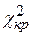 (
( , k):
, k):
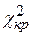 (
( , k) =
, k) = 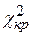 (0,05; 4) = 9,5.
(0,05; 4) = 9,5.
6. Так как  >
> 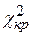 , то гипотезу Н 0 о нормальном распределении генеральной совокупности отвергаем. Другими словами, эмпирические и теоретические частоты различаются значимо.
, то гипотезу Н 0 о нормальном распределении генеральной совокупности отвергаем. Другими словами, эмпирические и теоретические частоты различаются значимо.
■
|
|
|
|
|
Дата добавления: 2014-10-15; Просмотров: 560; Нарушение авторских прав?; Мы поможем в написании вашей работы!