Определение. а) системы функций и являются полными

Определение.

Пример.

а) системы функци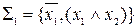й и 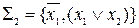являются полными. Доказать, что система 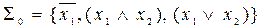также является полной.

Действительно, из законов де Моргана и двойного отрицания следует, что в каждой из этих двух систем недостающая до 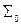функция выражается через остальные две: 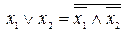, 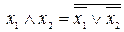. Следовательно, булева формула 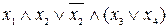в системе 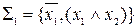перейдет в формулу 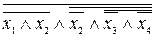, а в системе 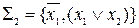- в формулу .

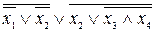Система функций 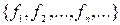из 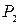, суперпозицией которых может быть представлена любая функция из некоторого множества булевых функций и в которой допускаются константы 0 и 1, называется ослаблено функционально полной или функционально полной в слабом смысле.

В терминах замкнутого класса можно дать следующее определение полноты.

Система булевых функций 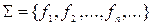называется функционально полной, если .

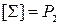Исходя из рассмотренных определений можно предположить, что не каждая система является полной. Пост предложил и исследовал условия, называемые критерием полноты, выполнение которых позволяет определить, является ли произвольная система булевых функций полной в сильном смысле.

Рассмотрим теорему полноты Поста, которая является основной теоремой о функциональной полноте булевых функций.

Теорема Поста о функциональной полноте.

Для того чтобы система функций 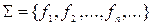была функционально полной, необходимо и достаточно, чтобы она содержала хотя бы одну функцию, не сохраняющую ноль, хотя бы одну функцию, не сохраняющую единицу, хотя бы одну несамодвойственную функцию, хотя бы одну немонотонную функцию, хотя бы одну нелинейную функцию.

Одна и та же функция может представлять в функционально полной системе одно или несколько требуемых свойств, а также может обладать всеми пятью требуемыми свойствами. Следовательно, минимальное число булевых функций в функционально полном наборе равно единице.

Если каждая из взятых функций обладает лишь одним свойством (но каждая другим), то для функциональной полноты необходима система из 5-ти функций.

Говорят, что функционально полная система функций образует базис в логическом пространстве.

Дата добавления: 2014-10-22