Нелинейная регрессия

В практических исследованиях использование линейных моделей для моделирования экономических зависимостей во многих случаях дает вполне удовлетворительный результат. Линейные модели в силу свой простоты, четкой экономической интерпретации параметров широко используются для анализа и прогнозирования. Однако зависимости между многими экономическими явлениями имеют нелинейный характер, и использование линейной модели не позволит неадекватно отобразить исследуемое явление. Примером нелинейной зависимости может служит зависимость урожайности от количества осадков, спрос на товар от его цены и т.д. Поэтому ограничиться рассмотрением только линейных регрессионных моделей невозможно.

Говоря о линейности модели, этот термин можно отнести как к независимым переменным модели, так и к ее параметрам. Различают два класса нелинейных регрессии:

- нелинейные относительно объясняющих переменных, но линейные по оцениваемым параметрам;

- нелинейные по оцениваемым параметрам.

Класс регрессий, нелинейных относительно включаемых в нее объясняющих переменных, но линейных по оцениваемым параметрам, включает уравнения, в которых зависимая переменная линейно связана с параметрами. Примером таких регрессий могут служить:

полиномы разных степеней - ;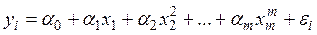

равносторонняя гипербола - .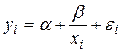

К классу регрессий, нелинейных по оцениваемым параметрам относятся уравнения, в которых зависимая переменная нелинейно связана с параметрами. Примером таких регрессий являются функции:

степенная - ;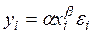

показательная - ;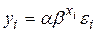

экспоненциальная - .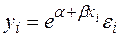

При оценке параметров регрессий, нелинейных по объясняющим переменным, используется метод замены переменных. Суть которого состоит в заменен нелинейных объясняющих переменных новыми линейными переменными, в результате чего нелинейная регрессия сводится к линейной. К новой, преобразованной модели может быть применен обычный метод наименьших квадратов. Например, в полиноме второго порядка

,

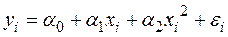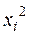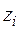
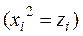заменяя переменную на , получим двухфакторное уравнение линейной регрессии:

,

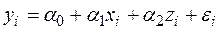для оценки параметров которого может быть применен обычный МНК.

Полином любого порядка сводится к линейной регрессии с ее методами оценивания параметров и проверки гипотез. Среди нелинейной полиномиальной регрессии чаще всего используется парабола второй степени, в отдельных случаях – полином третьего порядка. Ограничение в использовании полиномов более высоких порядков связано с требованием однородности исследуемой совокупности: чем выше порядок полинома, тем больше изгибов имеет кривая и, соответственно, менее однородна совокупность по результативному признаку.

Парабола второй степени целесообразна к применению, если для определенного интервала значений фактора меняется характер связи с результатом: прямая связь меняется на обратную или обратная на прямую. Например, изменение заработной платы работников физического труда от возраста. С увеличение возраста повышается заработная плата ввиду одновременного увеличения опыта и повышения квалификации работника. Однако с определенного возраста ввиду старения организма и снижения производительности труда дальнейшее повышение возраста может приводить к снижению заработной платы. Значение фактора, при котором достигается максимальное (или минимальное) значение результативного признака, определятся приравниванием к нулю первой производной второй степени.

Ввиду симметричности кривой параболу второй степени далеко не всегда можно использовать в конкретных исследованиях. Чаще исследователь имеет место лишь с отдельными сегментами параболы, а не с полной параболической формой. Поэтому если исходные данные не обнаруживают изменения направленности связи, то параметры параболы второй степени становятся трудно интерпретируемыми, а форма связи может быть заменена другими нелинейными моделями.

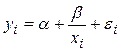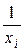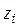
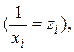Для равносторонней гиперболы , заменяя на получим линейное уравнение регрессии 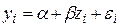, для оценки параметров которого может быть использован обычный МНК.

Равносторонняя гипотеза может быть использована, например, для характеристики связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции. Также примером использования равносторонней гиперболы являются кривые Филлипса (показывает взаимное изменение уровней безработицы и инфляции в экономике) и Энгеля (показывает величину расходов на товары в зависимости от роста дохода).

Регрессии, нелинейные по оцениваемым параметрам, подразделяются на два типа:

- нелинейные модели внутренне линейные;

- нелинейные модели внутренне нелинейные.

Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду (например, логарифмированием или заменой переменных). Примером регрессии, нелинейной по параметрам, но внутренне линейной, является степенная функция, которая широко используется в эконометрических исследованиях при изучении зависимости спроса от цены: 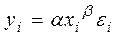, где y – величина спроса, х - цена товара.

Данная модель нелинейна относительно оцениваемых параметров, так как включает параметры α и β неаддитивно. Однако ее можно считать внутренне линейной, ибо логарифмирование данного уравнения по основанию е приводит его к линейному виду:

.

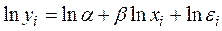Оценки параметров α и β в полученной линейной модели могут быть найдены с помощью МНК.

Широкое использование степенной функции 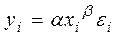связано с тем, что параметр β в ней имеет четкое экономическое истолковании, - он является коэффициентом эластичности. Это значит, что величина коэффициента β показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%.

Коэффициент эластичности можно определять и при других формах связи, но только для степенной функции он представляет собой постоянную величину, равную параметру β.

В рассматриваемой выше степенной функции предполагается, что случайная составляющая ε_i мультипликативно связана с объясняющей переменной х. Если же модель представить в виде 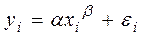, то она становится внутренне нелинейной, так как ее невозможно преобразовать в линейный вид.

Внутренне нелинейными будут и модели вида

, ,

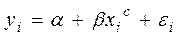потому, что эти уравнения не могут быть преобразованы в уравнения, линейные по коэффициентам.

Если же нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции и для оценки ее параметров используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода.

В моделях, нелинейных по оцениваемым параметрам, но приводимых к линейному виду, метод наименьших квадратов применяется к преобразованным уравнениям. Если в линейной модели и моделях, нелинейных по переменным, при оценке параметров исходят из критерия 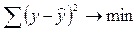, то в моделях, нелинейных по оцениваемым параметрам, требование МНК применяется не к исходным данным результативного признака, а к их преобразованным величинам, т.е. lny, 1/y. Так в степенной функции 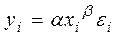оценка параметров основывается на минимизации суммы квадратов отклонений в логарифмах:

.

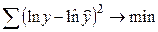Соответственно, если в линейных моделях (включая нелинейные по переменным) 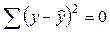, то в моделях, нелинейных по оцениваемым параметрам, 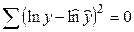, а 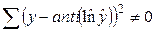. Вследствие этого оценка параметров для линеаризуемых функций методом наименьших квадратов оказывается несколько смещенной.

Дата добавления: 2014-10-22