Понятие задачи Коши

(О.Л.Коши (1789-1857) – выдающийся французский математик).

Отметим задачу, называемой задачей Коши для дифференциального уравнения первого порядка. Она гласит:

Требуется найти решение у = у(х) данного дифференциального уравнения, удовлетворяющего начальному условию у(х₀) = у₀, где (х₀;у₀) – заданная точка плоскости(х;у).

Конечно, в каждом данном случае задача Коши может иметь и не иметь решение. Если задача Коши имеет решение, то важно выяснить, единственно ли оно. Уже сейчас мы отметим важный факт, который будет для дифференциального уравнения первого порядка в разрешенной относительно у^/ форме иметь вид:

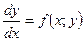, ((х;у)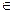G)

Задача имеет решение и притом единственное для любой точки (х₀;у₀) области G плоскости (х;у), если заданная на этой плоскости функция f(х;у) непрерывна вместе со своей частной производной .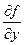

Конечно, единственность решения задачи Коши надо понимать в том смысле, что если у(х) и у₁(х) суть ее решения, удовлетворяющие одному и тому же начальному условию (у(х₀) = у₁(х₀) = у₀), заданные соответственно на интервалах (а;b) и (c;d), то

у(х) = у₁(х) на пересечении этих интервалов.

Основные тины дифференциальных уравнений:

• Уравнения с разделяющимися переменными
• Однородные уравнения

1) Уравнения с разделяющимися переменными.

Уравнениями с разделяющимися переменными называются уравнения вида 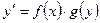, где - непрерывна на некотором 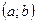, а непрерывна на 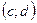, причем 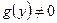на .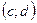

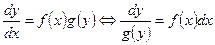(метод разделения переменных).

Интегрируя обе части, получаем .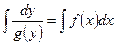

Обозначая 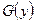любую первообразную для , а 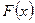- любую первообразную для , перепишем это уравнение в виде неявно выраженной функции 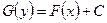. Это – искомая интегральная кривая.

Например:

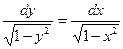интегрируя, получим

.

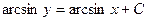Возьмем синус от обеих частей алгебраического уравнения: 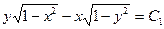(общее решение в неявном виде).

Дата добавления: 2014-10-22