Теорема и вектор Пойнтинга в стационарном электромагнитном поле

.

ВОЛНОВЫЕ УРАВНЕНИЯ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ.

В лекции изложены волновые уравнения электромагнитного поля и уравнения Гельмгольца, а также понятие вектора Пойнтинга и теорема Пойнтинга в стационарном электромагнитном поле..

Запишем следующие уравнения Максвелла для сред с неизменными значениями , :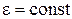

,

.

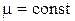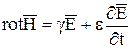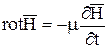Решим совместно эти уравнения. Для этого возьмем rot от левой и правой частей:

.

Учтем, что

,

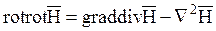а в однородной среде

.

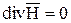Тогда:

Полученное уравнение для вектора 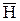называютволновым:

.

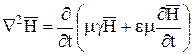Аналогичное уравнение можно получить и для вектора :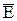

.

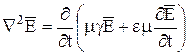Решениями этих уравнений в общем случае являются волновые функции, в аргументы которых входят линейные комбинации переменных — времени t и пространственных координат x, у, z.

Рассмотрим приведенные выше волновые уравнения и в синусоидальных полях и сделаем прямой переход к их сим­волической форме записи .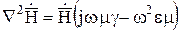

Обозначим 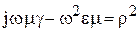. Тогда волновые уравнения для векторов 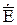и примут вид:

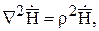
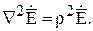
Эти уравнения носят названиеуравнений Гельмгольца. В этих уравнениях параметр

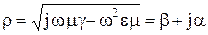
называют коэффициентом распространения; 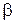— коэффициентом затухания; 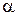- коэффициентом фазы.

В основе теоремы Пойнтинга лежит закон сохранения энергии. Теорема носит фундаментальный характер и имеет большое прикладное значение. Она часто используется при расчетах параметров, энергий и сил в различных электротехнических устройствах.

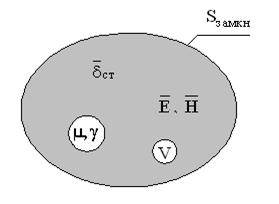
Рис. 22

Сущность теоремы покажем на примере объема V, ограни­ченного замкнутой поверхностью S, с характеристиками физических свойств 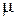, 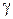(рис. 22). В этом объеме сторонний источ­ник (например, в виде 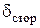) возбуждает поле тока и, как следствие, магнитное стацио­нарное поле. В самом общем виде можно утверждать, что часть энергии, выделяемая источником 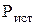, расходуется на джоулево тепло в объеме V, а остальная часть энергии затрачивается на тепло за пределами этого объема. В частности, на рис. 23

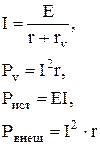
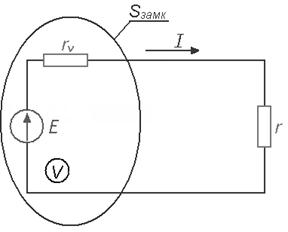
Рис. 92

Рис. 23

Так как часть мощности источников, расходуемая за пределами объема, вынуждена поки­нуть этот объем, пересекая по­верхность S, ее принято называть мощностью излучения. Тогда можно утверждать, что 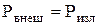и, следовательно,

.

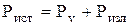Покажем, что выражения длявсех составляющих мощности могут быть получены в общем виде. Поле в объеме описывается уравнениями:

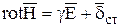
- закон полного тока,

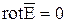
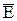-кулоновское потенциальное поле, и его rot равен нулю.

Решим совместно эти уравнения:

.

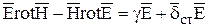Из курса математики известно, что в этом уравнения левая часть есть и, следовательно,

.

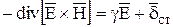Проинтегрируем левую и правую части уравнения по объему V:

.

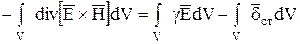Преобразуем левую часть с помощью теоремы Остроградского-Гауссa

.

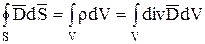В результате:

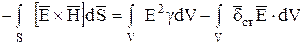
Векторное произведение

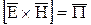
носит название —вектор Пойнтинга.

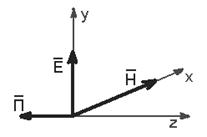
Рис. 24

Как видно (рис. 24), вектор 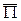перпендикулярен плоскости, составленной векторам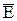ии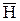, и имеет размер­ность поверхностной плотности мощности — В-А/м². Перепишем уравнение с учетом выражения для :

.

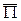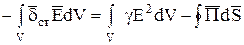Уравнение баланса мощности это и есть теорема Пойнтинга в стационарном поле. Назначение каждого слагаемого в ней очевидно:

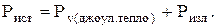
Таким образом, мощность излучения есть поток вектора Пойнтинга через замкнутую поверхность S, ограничивающую объем V.

Если в исследуемом объеме сторонние источники поля отсутствуют, то теорема Пойнтинга упрощается и принимает вид

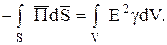
Это значит, что при отсутствии сторонних источников взятый с обратным знаком положительный поток вектора Пойнтинга, пронизывающий замкнутую поверхность S, равен джоулевым (тепловым) потерям в объеме, ограниченном этой поверхностью.

Если, например, объем V — проводник сечением S, длиной l с проводимостью 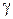, то

.

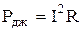Так как в рассматриваемом случае 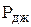равно потоку вектора Пойнтинга, сопротивление R объема V можно представить в виде:

.

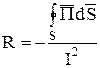Теорема Пойнтинга позволяет объяснить важные свойства, ка­сающиеся передачи электроэнергии от источника к приемнику.

Вернемся к приведенному выше примеру. Рассмотрим объем V с сопротивлением r (рис. 25) и запишем теорему Пойнтинга для этого объема

.

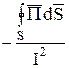Согласно этой теореме, мощность в сопротивление поступает из окружающего пространства, проникая через поверхность S. Вместе с тем замкнутая поверхность S не является однородной. Часть поверхности, охватывающей проводник с током, определяется удвоенным поперечным сечением провода, а большая ее часть – это любая мысленная поверхность в окружающем пространстве.

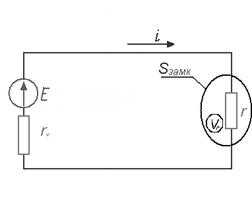Рис.25

По каким путям поступает мощность в объем проводника? Для этого решим следующую конкретную задачу. Цилиндрический провод (рис. 26) обтекается током l, удельная проводимость провода - 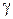. Определить поток вектора Пойнтинга через замкнутую поверхность, охватывающую провод на длине l. Очевидно, что эта замкнутая поверхность будет состоять из двух торцевых и боковой поверхностей .

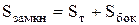Рис. 26

Теперь нужно рассчитать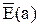,,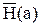 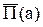на поверхности провода и 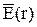, , 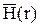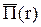внутри него, а затем найти соответствующие составляющие потока вектора Пойнтинга (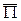) через замкнутую поверхность. Рассмотрим произвольную точку внутри провода и определим направления векторов 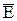, , 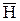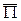. Исходя из условий осевой симметрии:

.

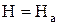Так как

,

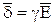то 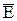направлена вдоль оси провода. Очевидно, что вектор 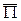лежит в плоскости поперечного сечения провода, а это значит, что его поток через торцевые сечения равен нулю. Но если это так, то мощность в объем провода поступает из окружающего пространства через боковую поверхность провода и расходуется там на тепло. Таким образом, поскольку

, , ,

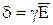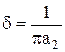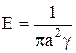то

.

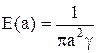В окружающем пространстве напряженность магнитного поля в силу осевой симметрии будет изменяться так же, как в поле линейного провода с током I:

.

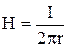На поверхности провода

,

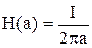отсюда

.

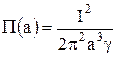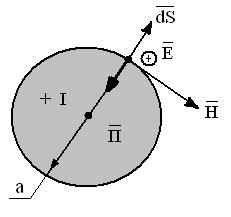
Рис. 27

На боковой поверхности 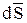направлен в сторону внешней нормали (рис. 27), а 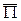вглубь провода. Тогда на боковой поверхности

,

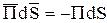причем на всей боковой поверхности

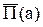=const.

В итоге

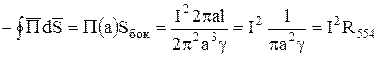
Этот пример говорит о том, что направление вектора Пойнтинга одновременно указывает и нанаправление передачи потока энергии, а величина его определяет интенсивность этого потока или поверхностную плотность мощности излучения.

Теорема и вектор Пойнтинга в комплексной форме. Пусть вновь, как и в стационарных полях, в некотором объеме V (ω, μ, γ, ε), ограниченном замкнутой поверхностью S (рис. 104), сторонними токами 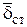возбуждено электромагнитное поле.

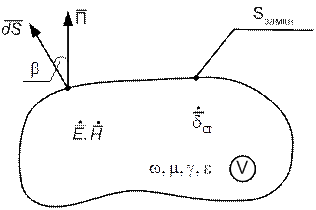
Рис. 28

Закон сохранения энергии позволяет утверждать, что мощность источников частично расходуется на тепло и изменение электри­ческой и магнитной энергий в объеме V, а оставшаяся часть излучается за пре­делы объема через поверхность, ограничивающую этот объем,

.

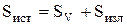Установим соотношения для этих мощностей. В качестве исходных, запишем уравнения Максвелла:

,

.

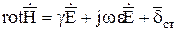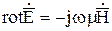Перепишем уравнение в сопряженных комплексах

.

.

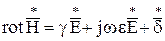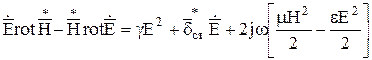В квадратных скобках выражения записана разность удельных магнитной и электрической энергий в объеме V, где 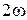— частота, с которой изменяются мгновенные значения этих энергий. Выше было показано, что левая часть уравнения раскрывается как 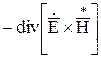. Заметим также, что комплексный вектор Пойнтинга определяется как

.

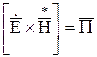Тогда:

.

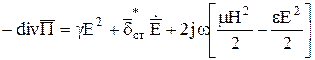Интегрирование (5.30) по объему V позволяет получить

.

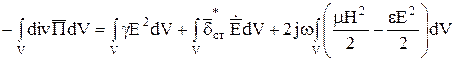К левой части (5.31) применим теорему Остроградского—Гаусса и перепишем в следующем виде:

.

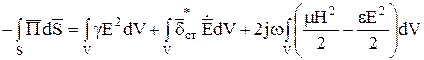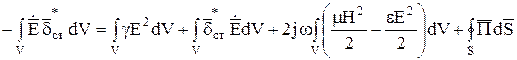
Выражение (5.32) и представляет собой теорему Пойнтинга для синусоидального электромагнитного поля. Здесь левая часть описывает комплексную мощность источников в объеме V. Первое слагаемое в правой части — мощность джоулевых потерь в объеме V,второе — реактивная мощность в объеме V. Как видно, в объеме V происходит обменный процесс энергиями между электрическими и магнитными полями, а также между полями и источниками. Далее под реактивной мощностью будем понимать мощность в синусоидальном режиме, которая появляется при изменении электрической или магнитной энергии. При этом обмен энергиями происходит с двойной частотой относительно источника поля. Очевидно, что третье слагаемое — это мощность излучения, определяемая как поток вектора Пойнтинга (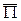) через замкнутую поверхность S.

Если в объеме V сторонние токи отсутствуют, теорема упрощается и принимает вид

.

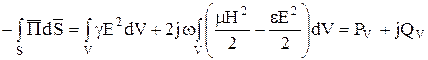Таким образом, следует, что взятый с обратным знаком положительный поток комплексного вектора Пойнтинга через замкнутую поверхность равен полной комплексной мощности, выделяемой в объеме V, ограниченном этой замкнутой поверхностью. Если, например, объем — это проводник, обтекаемый током I, то комплексное сопротивление этого проводника определяется как

.

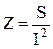Но если это так, то теорема Пойнтинга позволяет рассчитывать комплексные сопротивления различных устройств по формуле

.

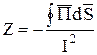Отметим, что теорема Пойнтинга в комплексной форме широко применяется при расчете и исследовании электротехнических устройств (электрических машин, трансформаторов, линий электропередач и т. д.).

Лекция 7

Дата добавления: 2014-10-22