Примеры решения задач. Задача 1. Определить натуральную величину отрезка прямой и углы его наклона к плоскостям проекций (метод прямоугольного треугольника)

Задача 1. Определить натуральную величину отрезка прямой и углы его наклона к плоскостям проекций (метод прямоугольного треугольника).

Дано: Решение:

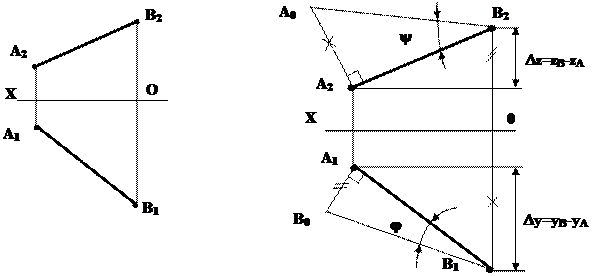
Рис.4.3

Строим прямоугольный треугольник, взяв за один катет горизонтальную (или фронтальную) проекцию отрезка - проекцию А₁В₁ (рис.4.3), а за другой – разность удалений концов отрезка от горизонтальной плоскости проекций Dz=z_В-z_А (или соответственно от фронтальной плоскости проекций - Dy=y_В-y_А). Величину Dz можно определить, проведя вспомогательную линию через один из концов отрезка перпендикулярно линии связи. Гипотенуза прямоугольного треугольного треугольника А₁В₁В_о и будет равна истинной величине отрезка АВ. Угол между гипотенузой и катетом, равным горизонтальной проекции отрезка, определяет величину угла наклона j заданного отрезка к горизонтальной плоскости проекций. Для определения угла наклона y к фронтальной плоскости проекций необходимо еще раз построить истинную величину отрезка с помощью прямоугольного треугольника А₂А₀В₂. При этом |А₀А₂|=|А₁В₀|. Если по условию задачи требуется определить только истинную величину отрезка прямой, достаточно построить прямоугольник на одной из проекций.

Задача 2. Разделить отрезок АВ точкой С в отношении 2:3 (рис.4.4).

Дано: Решение:

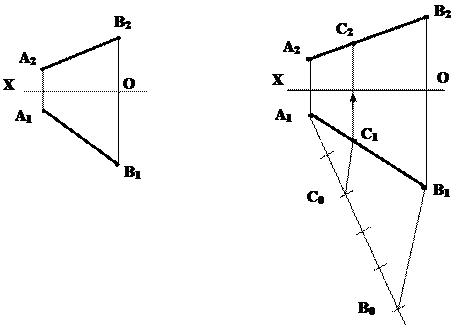Рис.4.4

Для того, чтобы построить точку С, делящую отрезок в заданном отношении, достаточно одну из проекций отрезка (на рис. 4.4) горизонтальная проекция) разделить в этом отношении, а затем построить вторую проекцию искомой точки, используя линию связи. Деление проекции А₁В₁ произведено с помощью теоремы Фалеса. Для этого из любого конца проекции А₁В₁, например из точки А₁ проводим луч под произвольным углом, на котором откладываем 2+3=5 равных отрезков произвольной длины. Соединяем точки В₀В₁, затем проводим через С₀ прямую С₀С₁||B₀B₁.

Задача 3. Достроить отрезок АВ, если длина его равна 50 мм (рис.4.5).

Задача является обратной к определению истинной величины отрезка прямой.

Рис.4.6

На прямой а зададимся произвольным отрезком АВ. С помощью прямоугольного треугольника А₁В₁В₀ определим истинную величину отрезка АВ. Далее от точки А₁ откладываем вдоль гипотенузы заданный отрезок 30 мм. Определяем искомую точку С(С₁,С₂), используя положение о пропорциональности деления отрезка, при этом С₀С₁||В₀В₁.

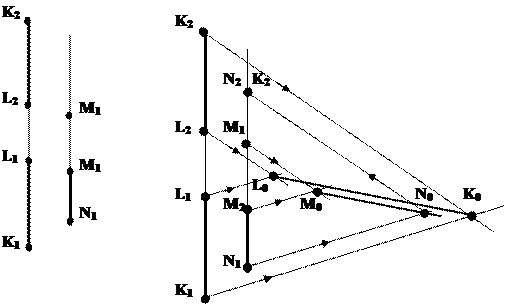
Задача 5. (Задача на профильные прямые). Достроить прямую NM, параллельную прямой КL (рис.4.7).

Замечание. Задачи на профильные прямые могут быть решены различными методами, в частности, с помощью построения третьей проекции этих прямых, либо с помощью методов косоугольного параллельного проецирования путем построения, так называемых, вспомогательных прямых. К этому типу задач следует отнести задача по определению взаимного положения профильных прямых, построения точки пересечения профильных прямых, а также ряд позиционных задач, связанных с построением точек пересечения профильной прямой и плоскости. Приведем решение задачи на профильные прямые методом построения вспомогательных прямых.

Дано: Решение:

Рис.4.7

Для того, чтобы построить недостающую фронтальную проекцию N₂ точки N, воспользуемся методом вспомогательных прямых. Суть его заключается в следующем. Для исходных профильных прямых методом косоугольного проектирования строятся вспомогательные прямые. По взаимному положению вспомогательных прямых судят о взаимном положении соответствующих им профильных прямых: если вспомогательные прямые параллельны, то параллельны соответствующие профильные прямые, если вспомогательные пересекаются, то исходные прямые или пересекаются или скрещиваются. Построим вспомогательную прямую для прямой KL. Для этого из точек K₁ и K₂ проведем лучи произвольного направления до пересечения в точке K₀. Точка К₀ – является вспомогательной для точки К. Аналогично строим точку L₀ – вспомогательную для точки L. При этом [L₁L₀)|| [K₁K₀), [L₂L₀)|| [K₂K₀). Прямая К₀L₀ является вспомогательной для прямой KL. Так как точка M, принадлежащая второй профильной прямой определена однозначно (известны обе ее проекции), построим вспомогательную ей точку М₀, при построении которой должна быть соблюдена параллельность проецирующих лучей на соответствующих проекциях: [М₁М₀)|| [K₁K₀)|| [L₁L₀) и [М₂М₀)|| [K₂K₀)|| [L₂L₀). Так как исходные прямые должны быть параллельны, поэтому через построенную точку М₀ зададим направление вспомогательной прямой М₀N₀, параллельно прямой K₀L₀. Для нахождения точки L₀ проведем проецирующий луч из точки L₁, параллельно лучам на горизонтальной проекции до пересечения с прямой, проведенной из точки M₀. Точка пересечения L₀будет являться вспомогательной для точки L, с помощью которой отыскивается неизвестная фронтальная проекция L₂ точки L.

Дата добавления: 2014-10-23