
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 6. Пределы и непрерывность
|
|
|
|
Функция, способы ее задания, свойства, график функции, преобразование графика сдвигом и деформацией.
Если 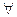 х
х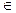 Х по закону f ставится (ставят) в соответствие единственное действительное у
Х по закону f ставится (ставят) в соответствие единственное действительное у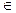 У, то говорят, что на множестве Х задана функция аргумента х. Пишут так у=f(x).
У, то говорят, что на множестве Х задана функция аргумента х. Пишут так у=f(x).
(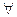 х
х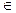 Х читаем так: для любого х из множества Х)
Х читаем так: для любого х из множества Х)
Множество Х принято называть областью определения функции. Она может быть задана или ее находят, используя вид функции. Множество У называют областью значений. Иногда область значений находят или она известна.
Например, областью определения функции y=lnx являются положительные действительные числа (пишут так х>0). Областью значений этой функции будут все действительные числа.
В обозначении у=f(x) содержится двусмысленность. Дело в том, что f (закон) - это фактически перечень правил, в строгой последовательности выполнения которых получаем единственное действительное значение у для произвольно взятого значения х из Х. Т.е. записано «число равно закону», что фактичеки неверно, но исторически принято считать приемлемой такую запись. Поэтому часто в литературе можно встретить и запись вида у=у(х), что также считается приемлемым. Просто не следует забывать, что есть что в записи у=f(x) (или у=у(х)).
Рассматривают несколько способов задания функции. Аналитический – с помощью одной или нескольких «формул». При этом запись вида у=f(х) рассматривают как явный способ задания функции. Если же переменных х и у связаны уравнением с двумя переменными, то говорят о неявном способе задания функии (Фактически, записав у=f(х) в виде у-f(х)=0 или f(х)-у=0 мы получаем неявное задание функции). Если же переменные (аргумент и функцию удобно связать соотношениями 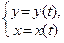 то говорят о параметрическом задании функции (связь реализована через параметр t).
то говорят о параметрическом задании функции (связь реализована через параметр t).
|
|
|
Из других способов задания функции отметим табличный способ и программный. В первом случае функция представляет собой таблицу с одним входом (столбец значений аргумента) и одним выходом (столбец значений функции). А во втором результат вычислений представлен либо цифровыми данным на экране или в файле.
Графиком функции называют кривую в избранной системе координат. При этом каждая точка кривой имеет координаты х и у, связанные законом f.
Опр. Пусть 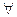 х
х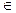 Х
Х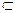 R задана у=f(х). Пусть
R задана у=f(х). Пусть 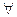 t
t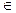 T
T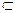 R задана x=ф(t). Тогда говорят, что на T задана сложная функция аргумента t и обозначают этот факт так y=f(ф(t)).
R задана x=ф(t). Тогда говорят, что на T задана сложная функция аргумента t и обозначают этот факт так y=f(ф(t)).
При этом х называют промежуточным аргументом, а t – основным. Закон f(ф(t)) называют наложением (суперпозицией) функций.
Пример 3.1. y=Sin ln(1-x2). Имеем функцию y=Sinz с промежуточным аргументом z=lnu, функцию z=lnu с промежуточным аргументом u=1-x2 и функцию u=1-x2 с основным аргументом х. Или просто сложную функцию у от аргумента х.
Пусть 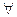 х
х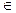 Х
Х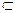 R задана у=f(х). Пусть мы смогли решить уравнение у=f(х) относительно переменной х. Т.е. получили запись х=ф(у). Т.к. оба равенства у=f(х) и х=ф(у) дают один и тот же график, но во втором случае аргументом будет переменная у, это неудобно (не принято так писать). Тогда можно в записи х=ф(у) поменять местами переменные х и у и получить привычную запись функции у=ф(х).
R задана у=f(х). Пусть мы смогли решить уравнение у=f(х) относительно переменной х. Т.е. получили запись х=ф(у). Т.к. оба равенства у=f(х) и х=ф(у) дают один и тот же график, но во втором случае аргументом будет переменная у, это неудобно (не принято так писать). Тогда можно в записи х=ф(у) поменять местами переменные х и у и получить привычную запись функции у=ф(х).
Определение. Две функции у=f(х) и у=ф(х) принято называть взаимно обратными функциями.
Отмечаем, что областью определения функции у=ф(х) будет область значений функции у=f(х). А областью значений функции у=ф(х) будет область определения функции у=f(х). Графики взаимно обратных функций симметричны относительно линии у=х (биссектрисы 1-го и 3-го координатных углов декартовой системы координат).
К простейшим свойствам функций относят: монотонность, периодичность, четность и нечетность.
Определение. Приращением переменной называют разность двух ее значений. Приращений обозначают символом  , за которым следует имя переменной. Например,
, за которым следует имя переменной. Например,  х – приращение переменной х (или просто дельта х).
х – приращение переменной х (или просто дельта х).
|
|
|
Определение. Если знаки приращения функции и аргумента в данной точке совпадают, то функция называется возрастающей в данной точке.
Аналогично дают определение убывающей в данной точке функции. Два этих понятия объединяют понятием монотонность.
Определение. Если f(x) определена на R и существует такое действительное Т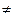 0, что f(x+Т)= f(x), то говорят, что f(x) периодическая с периодом Т (Т- периодической).
0, что f(x+Т)= f(x), то говорят, что f(x) периодическая с периодом Т (Т- периодической).
Периодические функции обладают свойствами.
Если f(x) Т- периодична, то она и nT- периодична. Док. Имеем f(x+nT)= =f((x+(n-1)T)+T)= f(x+(n-1)T)= f((x+(n-2)T)+T)=…= f(x+T)= f(x).
Если f(x) Т- периодична, то функция ф(х)= f(аx) Т/a –периодична. Док. Имеем ф(х+ Т/a)=f(a(x+ Т/a))=f(ax+T)=f(ax)=ф(х).
Определение. Если f(-x) = - f(x), то функцию называют нечетной.
Определение. Если f(-x) = f(x), то функцию называют четной.
При проверке свойства четности ответ следует давать только по четности. Это значит, что, если условие f(-x) = f(x) не выполняется, нельзя говорить ” Функция нечетная”, но следует говорить ”Функция не будет четной”, т.к. речь идет не о четных числах, а о свойстве четности. (Если проверяете пиджак, чистый ли он, то он может быть либо чистым либо грязным. И нет никакого дела, какого цвета пиджак).
При схематическом построении графиков функций следует использовать указанные свойства их. Помимо этого используют при схематическом построении (говорят о качественной картине без уточнения конкретных цифровых характеристик) наложение линейной функциональной зависимости на данную функцию. Это значит на основе базовой функции у= f(x) можно строить графики функций вида у=Аf(аx+b)+B. Выполним такое построение поэтапно, а затем запишем жесткий алгоритм построения графика функции у=Аf(аx+b)+B.
1.Пусть мы имеем базовый график (известный нам) у= f(x).
2.Для построения графика функции у= f(аx) достаточно график у=f(x) сжать вдоль оси Ох в направлении оси Оу в а раз при а>1 (растянуть график у=f(x) вдоль оси Ох от оси Оу в а раз при а <1). Если при этом а отрицательно, то следует деформируемый график еще и отразить в оси Оу.
3.Для построения графика функции у=Аf(x) достаточно график у=f(x) сжать вдоль оси Оу в направлении оси Ох в а раз при A<1 (растянуть график у=f(x) вдоль оси Оy от оси Оx в а раз при A>1). Если при этом A отрицательно, то следует деформируемый график еще и отразить в оси Оx.
|
|
|
4.Для построения графика функции у=f(x+м) достаточно сдвинуть базовый график у=f(x) на величину м вдоль оси Ох вправо, если м<0 и влево, если м>0.
5.Для построения графика функции у=f(x)+В достаточно сдвинуть базовый график у=f(x) на величину В вдоль оси Оу вниз, если В<0 и вверх, если В>0.
Общий алгоритм. Для построения графика функции у=Аf(аx+b)+B следует: переписать равенство в виде у=Аf(а(x+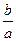 ))+B; построить базовый график у= f(x); выполнить п.п.2 и 3 в любой последовательности; выполнить п.п.4 и 5 в любой последовательности.
))+B; построить базовый график у= f(x); выполнить п.п.2 и 3 в любой последовательности; выполнить п.п.4 и 5 в любой последовательности.
Комментарий. При достаточном опыте построения графиков, последовательность можно изменить. Однако нужно помнить, что п.п. 2 и 3 не изменяют “точку опоры” (расположение начала системы координат) и потому последующий сдвиг легко и всегда правильно реализуется. Если же сначала произвести сдвиг кривой, то теряется возможность деформировать ее, т.к. становится неизвестным “куда сжимать”, хотя “вдоль чего” остается тем же. Неизвестной будет также ось отражения при необходимости.
Пример 3.2. Изобразите схематически (качественно) кривую
y=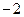 -3
-3 .
.
Решение. Построим сначала базовую кривую y=x1,5 . Это – парабола с вершиной в начале координат, проходящая через точки (0;0) и (1;1) как и всякая типовая парабола. Для отрицательных х кривой нет и график расположен в 1-й четверти. Ветви параболы загнуты вверх т.к. 1,5>1. Рисунок базовой кривой представлен на Рис 3.1.
 |

y=x1,5
 |
1 * (1;1)
 1
1
 |
Рис 4. Базовая кривая y=x1,5
Теперь строим график функции y=-3 x1,5. Растянув базовый график в 3 раза вдоль оси Оу от оси Ох и отразив его в оси Ох, получим кривую, представленную на Рис 4 –1. Масштаб возьмем несколько иной. Так как деформация и отражение завершены, можно выполнять сдвиг вдоль координатных осей: сдвинуть кривую на 1 вправо и опустить полученное на 2 вниз. Получим результативную (требуемую) кривую y=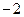 -3
-3 .
.
|
|
|
Отметим, что на всех графиках нанесена точка, обозначенная символом *, но с разными координатами. Сделано это умышленно, чтобы можно было проследить за преобразованием графика по отдельно взятой точке, т.к. в противном случае при всех преобразованиях парабола остается параболой и качественная картина ее не меняется

 1
1

 -1
-1
-----1 кривая y= -3x1,5

 -2
-2
 -3 * (1; -3)
-3 * (1; -3)
2 ------
 -5 * (2; -5)
-5 * (2; -5)
Рис 3.2. Кривые: y=-3x1,5 – 1; y=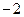 -3
-3 -2
-2
Основные элементарные функции и наиболее важные функции
Используя известные сведения и приведенный алгоритм, можно сделать обзор графиков некоторых важных в приложениях функций.
Определение. Назовем основными элементарными функциями такие: степенная у=ха (а- действительное); показательная у=ах (а>0 и а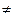 1); логарифмическая у=logax (а>0 и а
1); логарифмическая у=logax (а>0 и а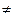 1); круговые тригонометрические y=Sinx, y=Cosx, y=tgx, y=ctgx; обратные тригонометрические y=arcSinx, y=arcCosx, y=arctgx, y=arcctgx. Они и служат базовыми при построении графиков других функций.
1); круговые тригонометрические y=Sinx, y=Cosx, y=tgx, y=ctgx; обратные тригонометрические y=arcSinx, y=arcCosx, y=arctgx, y=arcctgx. Они и служат базовыми при построении графиков других функций.
Определение. Все функции, которые получены из основных элементарных действиями сложения, вычитания, умножения, деления и наложения функциональной зависимости (суперпозиции), назовем элементарными.
Все остальные функции назовем неэлементарными.
Все степенные функции у=ха при а>0 имеют графики, которые условно можно назвать параболами. Схематическое их построение следует начинать с величины показателя а. Графики всех парабол проходят через две точки О(0;0) и А(1;1). При 0 < а < 1 ветви всех парабол изогнуты выпуклостью вверх, а при а >1 изогнуты выпуклостью вправо. После построения ветви параболы в
1-й четверти декартовой системы координат переходят к построению в других четвертях, используя свойство четности, нечетности и расположение области определения. Так, например, график функции y=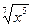 проходит через известные точки О и А, представлен выпуклой ветвью в 1-й четверти. Т.к. функция определена при любых х, то можно воспользоваться четностью и отразить центрально ветвь параболы из 1-й четверти в 3-ю (центр симметрии – начало координат точка О).
проходит через известные точки О и А, представлен выпуклой ветвью в 1-й четверти. Т.к. функция определена при любых х, то можно воспользоваться четностью и отразить центрально ветвь параболы из 1-й четверти в 3-ю (центр симметрии – начало координат точка О).
При отрицательном а графики степенных функций условно назовем гиперболами, т.к. схематически графики похожи на график обратно пропорциональной зависимости у=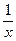 . Остальная схема построения графика изложена выше.
. Остальная схема построения графика изложена выше.
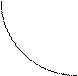
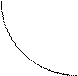
На основе графика функции у=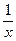 следует научиться строить график дробно-линейной функции у=
следует научиться строить график дробно-линейной функции у=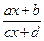 . Для этого сначала выполняют преобразование правой части равенства делением “уголком” и получают сумму целой части и правильной дроби. Затем приводят выражение к виду у=
. Для этого сначала выполняют преобразование правой части равенства делением “уголком” и получают сумму целой части и правильной дроби. Затем приводят выражение к виду у=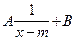 . Остается выполнить деформацию кривой у=
. Остается выполнить деформацию кривой у=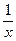 с коэффициентом А и затем реализовать сдвиг вдоль осей координат полученного графика.
с коэффициентом А и затем реализовать сдвиг вдоль осей координат полученного графика.
 |

 У у
У у
*(2;3)
 | |||
 | |||
* (1;1) + (0;1)
О х х
 |  | ||||
 |
+(-1;-1)
Рис 5. Базовая гипербола (слева) и преобразованная (справа)
Пример 3.3. Пусть нам требуется построить схематически график функции у=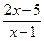 . Выделим целую часть. Получаем
. Выделим целую часть. Получаем
у=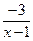 +2
+2
Выполним растяжение графика с левого рисунка в 3 раза вдоль Оу от Ох. Затем полученную кривую сдвинем вправо на 1 и вверх на 2. Получим правую кривую. При необходимости можно вычислить координаты точек пересечения результативной кривой с осями координат.
Показательную функцию у=ах (а>0 и а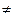 1) часто называют экспонентой и обозначают так у=ехрах. Отметим, что все экспоненты проходят через точку (0;1). При 0 < а < 1 экспоненты убывают, но остаются положительными, а при
1) часто называют экспонентой и обозначают так у=ехрах. Отметим, что все экспоненты проходят через точку (0;1). При 0 < а < 1 экспоненты убывают, но остаются положительными, а при
а >1 все экспоненты возрастают, оставаясь положительными. Легко видеть, что при очень больших а и при очень малых а (но всегда положительных!) графики экспонент очень “крутые”. При а близких к 1 графики очень “пологие” и прижимаются к горизонтальной прямой у=1. Норвежский математик Непер предположил, что существует такое основание а, при котором касательная к экспоненте в точке (0;1) образует угол 45о с осью Ох. При дальнейших исследованиях выяснилось, что таким числом будет иррациональное число, значение которого приближенно равно 2,71828…. Это число принято называть числом Непера и обозначать буквой е. Т.о. имеем приближенное равенство
е= 2,71828…. Показательная функция с таким основанием записывается так у=ех или у=ехрх.
Графики экспонент приводить не будем в силу их общеизвестности.
Логарифмическая функция y=logax (а>0 и а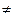 1) определяется (договор!) как обратная к экспоненте и потому подчиняется все свойствам обратной функции: область определения y=logax – положительные х (т.е. область значений экспоненты); график y=logax симметричен графику экспоненты относительно биссектрисы у=х первого и третьего координатных углов. Это значит, что все логарифмики (графики логарифмических функций) проходят через точку (1;0). При 0 < а < 1 все логарифмы – убывающие функции, а при а >1 все логарифмы возрастающие функции. И при этом все графики расположены правее оси Оу. Наиболее широко используют логарифмы по основаниям 10 (обозначение y=lgx) и натуральные (непрерывны) логарифмы (обозначение lnx). Последняя логарифмика обладает свойством – касательная к этой кривой в точке (1;0) проходит под углом 45о к оси Ох. Эта функция, наряду с функцией у=ех (или у=ехрх) наиболее применяемы в технических приложениях математики.
1) определяется (договор!) как обратная к экспоненте и потому подчиняется все свойствам обратной функции: область определения y=logax – положительные х (т.е. область значений экспоненты); график y=logax симметричен графику экспоненты относительно биссектрисы у=х первого и третьего координатных углов. Это значит, что все логарифмики (графики логарифмических функций) проходят через точку (1;0). При 0 < а < 1 все логарифмы – убывающие функции, а при а >1 все логарифмы возрастающие функции. И при этом все графики расположены правее оси Оу. Наиболее широко используют логарифмы по основаниям 10 (обозначение y=lgx) и натуральные (непрерывны) логарифмы (обозначение lnx). Последняя логарифмика обладает свойством – касательная к этой кривой в точке (1;0) проходит под углом 45о к оси Ох. Эта функция, наряду с функцией у=ех (или у=ехрх) наиболее применяемы в технических приложениях математики.
Круговые тригонометрические функции y=Sinx, y=Cosx,y=tgx, y=ctgx известны из школьного курса. Отметим лишь, что они периодические и потому обладают специфическими свойствами (см. 3.2.1). И что они по интервально монотонны.
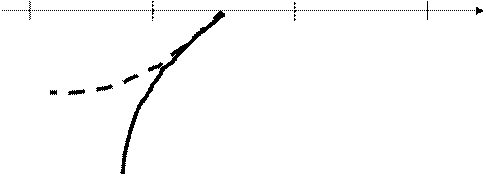
На основании круговых тригонометрических функций строятся обратные для них: y=arcSinx, y=arcCosx, y=arctgx, y=arcctgx. Графики обратных тригонометрических функций строят только для того участка области определения основной функции, на котором основная функция монотонна. Сначала строят монотонную часть основной функции. Затем полученный график отражают в биссектрисе 1-го и 3-го координатных углов. Ниже приведены рисунки построенных взаимно обратных функций y=Sinx и y=arcSinx, а также y=tgx и y=arctgx. Аналогично строятся графики функций
 Y=arcCosx y=arcctgx.
Y=arcCosx y=arcctgx.
 Y
Y
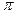 /2 y=arcSinx
/2 y=arcSinx


у=x
 y=Sinx
y=Sinx
 1
1 
- /2 -1 1
/2 -1 1  /2 X
/2 X
 |
 -1
-1
 -
- /2
/2
 |


 Y
Y
Y=tgx y=x

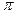 /2
/2


 y=arctgx
y=arctgx
 -
- /2
/2 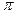 /2 X
/2 X
 |
-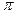 /2
/2

Рис 6. Примеры построения обратных функций
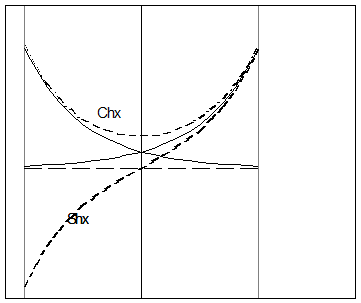
В математических приложениях применяются гиперболические функции. Рассмотрим только две из них y=Shx (гиперболический синус) и y=Chx (гиперболический косинус). Эти две функции определяются равенствами y=Shx=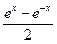 и y=Chx=
и y=Chx=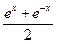 . В отличие от круговых тригонометрических функций (функций в круге), обладающих свойством Cos2x +Sin2x =1, гиперболические обладают свойством Cos2x - Sin2x =1. Первое из известных тождеств похоже на уравнение окружности с центром в начале координат и единичным радиусом (поэтому и функции в круге или круговые). А второе похоже на каноническое уравнение гиперболы (а потому и функции гиперболические). Графики этих функций строят схематически, используя принцип «суммирования ординат».
. В отличие от круговых тригонометрических функций (функций в круге), обладающих свойством Cos2x +Sin2x =1, гиперболические обладают свойством Cos2x - Sin2x =1. Первое из известных тождеств похоже на уравнение окружности с центром в начале координат и единичным радиусом (поэтому и функции в круге или круговые). А второе похоже на каноническое уравнение гиперболы (а потому и функции гиперболические). Графики этих функций строят схематически, используя принцип «суммирования ординат».
 |
 |
Рис 7. Построение Shx и Сhx суммированием экспонент 0,5е-х и 0,5ех
Известно, что линейная комбинация гармоник одинаковой частоты есть гармоника той же частоты. В самом деле
aSinkt+bCoskt=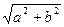 (
(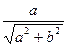 Sinkt+
Sinkt+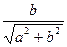 Coskt) =
Coskt) =
=A(CosфSinkt+Sinф Coskt)=Asin(kt+ф). В самом деле, выражения 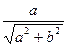 и
и 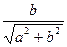 по модулю не превосходят 1, а в сумме дают 1. Поэтому они могут быть истолкованы как синус и косинус (в любом порядке; в данном случае они истолкованы так
по модулю не превосходят 1, а в сумме дают 1. Поэтому они могут быть истолкованы как синус и косинус (в любом порядке; в данном случае они истолкованы так 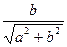 =Sinф
=Sinф 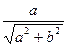 =Cosф). Далее применена формула синуса суммы двух углов (а может быть применена формула разности углов). Величина А, полученная в результате преобразования, носит название амплитуды гармоники k - частоты.
=Cosф). Далее применена формула синуса суммы двух углов (а может быть применена формула разности углов). Величина А, полученная в результате преобразования, носит название амплитуды гармоники k - частоты.
Руководствуясь такой схемой можно утверждать качественно, что графиком функции f(x)=ex Sin(kx+ф) будет график затухающиих (при < 0) или развивающихся (при > 0) колебаний, т.к. ex может быть истолкована как амплитуда этих колебаний.
Контрольные вопросы и задания для самостоятельной подготовки:
1. Множества. Обозначения. Логические символы. Операции над множествами.
2. Вещественные числа и их основные свойства.
3. Числовая прямая.
4. Абсолютная величина числа.
5. Понятие функции.
6. Числовые функции. Способы задания функций.
7. Ограниченность, монотонность, четность и периодичность функции.
8. Обратная функция. Простейшие элементарные функции.
9. Сложная функция.
10. Рациональные функции.
11. Класс элементарных функций.
12. Преобразование графиков функций.
13. Дана функция 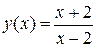 . Найти
. Найти 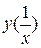 .
.
14. Найти область определения функции 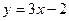
15. Найти область определения функции 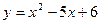
16. Найти область определения функции 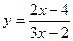
17. Найти область определения функции 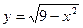
18. Найти область определения функции 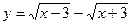
19. Найти область определения функции 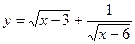
20. Найти область определения функции 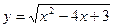
21. Найти область определения функции 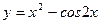
22. Найти область определения функции 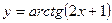
23.Найти область определения функции 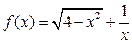
24.Найти область определения функции 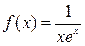
25.Найти область определения функции
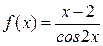
26. Найти область определения функции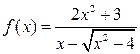
27. Найти область определения функции 
28. Найти область определения функции 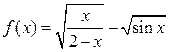
29. Найти область определения функции 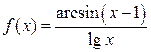
30. Найти область определения функции 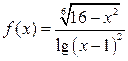
31. Найти область определения функции 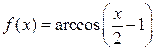
32. Найти область определения функции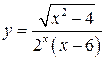
Рассматривается понятие предела числовой последовательности. Предел функции в бесконечности и в точке. Непрерывность функции в точке. Свойства числовых множеств и последовательностей. Бесконечно малые и бесконечно большие величины. Основные теоремы о пределах. Признаки существования предела. Замечательные пределы. Глобальные свойства непрерывных функций.
|
|
|
|
|
Дата добавления: 2014-10-23; Просмотров: 461; Нарушение авторских прав?; Мы поможем в написании вашей работы!