Тема: наближення інтерполяції та точні оцінки похибок інтерполювання

Лабораторна робота 10.

Завдання.

Контрольні питання.

1. В чому полягає задача інтерполяції?

2. Визначить вузли інтерполяції, інтерполюючу функцію, інтерполяційниймногочлен.

3. Що таке інтерполяційна формула?

4. Визначитьподілені різниці нульового порядку, поділені різниці k – го порядку.

5. Запишіть інтерполяційну формулу Ньютона з поділеними різницями.

6. Чи є необхідним для обчислення таблиці поділених різниць, щоб всі вузли інтерполяції були попарно відмінними?

7. Чи можна отримати поділену різницю порядку 10, якщо дано 10 вузлів інтерполяції?

8. Чи можна отримати будь – яку поділену різницю порядку 10, якщо дано 11 попарно відмінних вузлів інтерполяції?

9. Чи всі поділені різниці порядку 10 знаходяться у таблиці поділених різниць, якщо дано 11 попарно відмінних вузлів інтерполяції?

10. Чи можна додати ще один вузол інтерполяції у таблицю поділених різниць у довільне місце, чи лише в кінці таблиці (як у задачі 2)?

11. Якщо треба виписати інтерполяційну формулу Ньютона, то чи потрібні інші елементи таблиці поділених різниць, окрім одного її рядка?

12. Чи можна, обчислюючи таблицю поділених різниць, обмежитись одним її рядком?

Задача. 1. Для функції f, заданої наступною таблицею, знайти такі її поділені різниці.

2. Записати інтерполяційну формулу Ньютона з поділеними різницями для функції f,

заданої такою таблицею.

Варіант 1.

i
xi	2,31	4,72	7,83	5,82	6,46
yi	0,837248	1,551809	2,057963	1,7613	1,865629

поділені різниці: f (x₂; x₃; x₄), f (x₀; x₁; x₂; x₃), f (x₀; x₁; x₂; x₃; x₄), f (x₀; x₁; x₃; x₄)

Варіант 2.

i
xi	3,12	7,42	8,73	8,52	4,66
yi	0,021591	0,907299	0,640215	0,786288	-0,99863

поділені різниці: f (x₁; x₂; x₃), f (x₁; x₂; x₃; x₄), f (x₀; x₁; x₂; x₃; x₄), f (x₁; x₂; x₄)

Варіант 3.

i
xi	3,12	7,42	8,73	8,52	4,66
yi	0,021591	0,907299	0,640215	0,786288	-0,99863

поділені різниці: f (x₁; x₂; x₃), f (x₁; x₂; x₃; x₄), f (x₁; x₂; x₃; x₄; x₀), f (x₃; x₄; x₀)

Варіант 4.

i
xi	1,23	2,47	3,78	2,58	1,37
yi	3,42123	11,82245	43,81604	13,19714	3,935351

поділені різниці: f (x₃; x₂; x₁), f (x₄; x₃; x₂; x₁), f (x₄; x₃; x₂; x₁; x₀), f (x₂; x₁; x₀)

Варіант 5.

i
xi	1,37	2,58	3,78	2,47	1,28
yi	0,979908	0,532535	-0,59592	0,622234	0,958016

поділені різниці: f (x₄; x₃; x₂), f (x₃; x₂; x₁; x₀), f (x₄; x₃; x₂; x₁; x₀), f (x₃; x₁; x₀)

Варіант 6.

i
xi	2,31	4,72	7,83	5,82	6,46
yi	0,837248	1,551809	2,057963	1,7613	1,865629

поділені різниці: f (x₁; x₂; x₃), f (x₁; x₂; x₃; x₄), f (x₁; x₂; x₃; x₄; x₀), f (x₃; x₄; x₀)

Варіант 7.

i
xi	3,12	7,42	8,73	8,52	4,66
yi	0,021591	0,907299	0,640215	0,786288	-0,99863

поділені різниці: f (x₃; x₂; x₁), f (x₄; x₃; x₂; x₁), f (x₄; x₃; x₂; x₁; x₀), f (x₂; x₁; x₀)

Варіант 8.

i
xi	1,37	2,58	3,78	2,47	1,28
yi	0,979908	0,532535	-0,59592	0,622234	0,958016

поділені різниці: f (x₃; x₂; x₁), f (x₄; x₃; x₂; x₁), f (x₄; x₃; x₂; x₁; x₀), f (x₂; x₁; x₀)

Варіант 9.

i
xi	1,23	2,47	3,78	2,58	1,37
yi	3,42123	11,82245	43,81604	13,19714	3,935351

поділені різниці: f (x₄; x₃; x₂), f (x₃; x₂; x₁; x₀), f (x₄; x₃; x₂; x₁; x₀), f (x₃; x₁; x₀)

Варіант 10.

i
xi	2,31	4,72	7,83	5,82	6,46
yi	0,837248	1,551809	2,057963	1,7613	1,865629

поділені різниці: f (x₃; x₂; x₁), f (x₄; x₃; x₂; x₁), f (x₄; x₃; x₂; x₁; x₀), f (x₂; x₁; x₀)

(2г.)

Мета: Отримати відомості про методи обчислення точних оцінок похибок

інтерполювання та навчитися застосовувати ці методи до конкретних задач.

Теоретичні відомості.

Нехай f (x) – задана функція, L_n(х) – інтерполяційний многочлен степеня n скажімо у

формі інтерполяційного многочлена Лагранжа

L_n(x) = 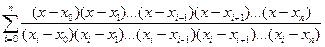f (x_i)

або у формі інтерполяційного многочлена Ньютона з поділеними різницями

L_n(x) = f (x₀) + f (x₀; x₁)(х – х₀) + … + f (x₀; x₁;…; x_n)(х – x₀)(х – x₁) … (х – х_n-1).

Нехай далі f (x) ≈ L_n(x) – відповідна інтерполяційна формула. Тоді

Означення. Різницю R_n(f,x) = f (x) – L_n (х) називають похибкою інтерполювання або залишковим членом інтерполяційної формули.

Теорема. (Оцінка похибки інтерполювання). Якщо вузли інтерполювання x_i (і = 0, 1, …, n) різні і належать відрізку [a; b], функція f (x) n + 1 раз неперервно диференційовна на [a; b], то похибка інтерполювання

R_n(f, x) = 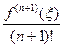ω_n+1(х), (1)

де ξ = ξ (x) є [a; b], ω_n+1(х) = (x – x₀)(x – x₁)…(x – x_n).

Зауважимо, що обчислювальна похибка інтерполяційної формули у комп’ютері не буває такою великою, щоби суттєво вплинути на результат, тобто за величиною зрівнятись з похибкою метода, оцінюваною у (1). Тому на відміну від ітераційних методів похибкою обчислень при інтерполюванні звичайно нехтують.

Хід роботи.

Задача 1. Нехай функція sin x задана таблично

i
xi	0,45	0,32	0,79	0,51	0,64
yi	0,434966	0,314567	0,710353	0,488177	0,597195

1. Записати інтерполяційну формулу Ньютона з поділеними різницями по заданій таблиці. 2. По цій формулі обчислити наближене значення в точці х = 0,58.

Розв’язання. Відповідна таблиця поділених різниць для заданої таблиці була отримана вже у задачі 1 лабораторної роботи 9:

	A	B	C	D	E	F
	х0	0,434966	0,926146	-0,2472	-0,14442	0,021447
	х1	0,314567	0,842099	-0,25586	-0,14034
	х2	0,710353	0,793486	-0,30077
	х3	0,488177	0,838601
	х4	0,597195

Тут потрібно, по – перше, виписати інтерполяційну формулу Ньютона:

f (x) ≈ L_n(x) = f (x₀) + f (x₀; x₁)(х – х₀) + … + f (x₀; x₁;…; x_n)(х – x₀)(х – x₁) … (х – х_n-1).

Оскільки за результатами розрахунків f (x₀) = 0,434966, f (x₀; x₁) = 0,926146, f (x₀; x₁; x₂) = – 0,2472, f (x₀; x₁; x₂; x₃) = – 0,14442, f (x₀; x₁; x₂; x₃; x₄) = 0,021447, то

f (x) ≈ 0,434966 + 0,926146(х – 0,45) – 0,2472(х – 0,45)(х – 0,32) – 0,14442(х – 0,45)(х – 0,32) (х – 0,79) + 0,021447(х – 0,45)(х – 0,32)(х – 0,79)(х – 0,51).

По – друге, треба знайти наближене значення функції sin x в точці х = 0,58. Нехай значення вузлів інтерполяції містяться додатково в діапазоні А16:Е16,

	A	B	C	D	E
	0,45	0,32	0,79	0,51	0,64

а задане значення х = 0,58 у чарунці А21. Тоді відповідні розрахунки можна виконати за допомогою наступної електронної таблиці:

	A	B	C	D	E
	= $А$21 – А16	→	→	→	→
		= A20*A19	→	→	→
	0,58	= СУММПРОИЗВ(A20:E20; A10:E10)

Тут у рядку 19 підраховуються значення у дужках (х – х_i) (i = 0, 1, 2, 3, 4); у рядку 20 множники на відповідні поділені різниці в інтерполяційній формулі Ньютона; у чарунці В21 шукане наближене значення f (0,58) по цій формулі. В результаті отримаємо:

	A	B	C	D	E
	0,13	0,26	-0,21	0,07	-0,06
		0,13	0,0338	-0,0071	-0,0005
	0,58	0,548024

Отже, sin 0,58 ≈ 0,548024.

Задача 2. За формулою (1) оцінити похибку, з якою значення sin 0,58 отримане у задачі 1. Скільки вузлів інтерполяції x_i треба застосувати, для того, щоби отримати це значення з точністю п’ятизначних математичних таблиць Брадіса.

Розв’язання. Тут f (x) = sin x, х = 0,58, n = 4. Тому за формулою (1) тут R₄(f, x) =

= ω₅(х), де ξ = ξ (x) є [0,32; 0,79]. Значення ω₅(х) = (х – x₀)(х – x₁) … (х – х₄) підрахуємо практично так само, як в задачі 1, у такій електронній таблиці:

	A	B	C	D	E
	= $А$21 – А16	→	→	→	→
	= A23	= A24*B23	→	→	→

Тут у рядку 23 підраховуються значення у дужках (х – х_i) (i = 0, 1, 2, 3, 4), у рядку 24 їх добутки ω_n(х); зокрема ω₅(х) отримаємо у чарунці E24. Маємо:

	A	B	C	D	E
	-0,13	-0,26	0,21	-0,07	0,06
	-0,13	0,0338	0,007098	-0,0005	-3E-05

Отже, ω₅(х) ≈ – 3∙10^-5. Таблиця для підрахунку 1/n! наступна

	A	B	C	D	E
		= А7*В6	→	→	→
	= 1/А7	→	→	→	→

В результаті дістанемо

	A	B	C	D	E
		0,5	0,166667	0,041667	0,008333

Отже, 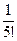≈ 0,008333. Далі │sin⁽⁵⁾(x)│=│cos x│≤ 1. Тож абсолютна похибка наближення для sin 0,58 │R₄(f, x)│ = 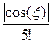│ω₅(х)│≤ 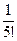│ω₅(х)│ ≈ 0,008333 ∙ 3 ∙ 10^-5 ≈ 2,4843∙10^-7. Таким чином наближення задачі 1 sin 0,58 ≈ 0,548024 має всі 6 вірних значущих цифр, що навіть перевищує вимоги п’ятизначних математичних таблиць Брадіса.

Чи можна зменшити кількість вузлів, якщо нам потрібні лише 5 вірних значущих цифр? Підрахуємо абсолютну похибку наближення │R₃(f, x)│ ≤ 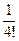│ω₄(х)│ ≈ 0,041667 ∙ 0,0005 ≈ 2,1∙10^-5. При такій похибці відповідне наближення для sin 0,58 буде мати лише 4 значущі цифри. Отже, для отримання необхідних 5 значущих цифр треба застосувати всі 5 вузлів інтерполяції з таблиці, заданої умовою задачі 1. Задачу розв’язано.

Дата добавления: 2014-10-31