Предел функции

Предел функции в точке

Пусть функция f (x) определена на некотором множестве X. Возьмем из Х последовательность точек

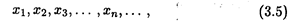
сходящуюся к точке а, причем а Х или a X. Соответ­ствующие значения функции в точках этой последовательности также образуют числовую последовательность

и правомерно рассмотреть вопрос о ее сходимости.

Определение. Число А называется пределом функции f (x) в точке а (или пределом функции при х 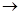а), если для любой cходящейся к а последовательности (3.5) значений аргумента х, отличных от а, соответствующая последовательность зна­чений функции (3.6) сходится к числу А.

Для обозначения предельного значения функции использу­ется следующая символика: f (x) 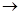А. Заметим, что функция f (x) может иметь в точке а только одно предельное зна­чение, поскольку последовательность f(x_n) имеет только один предел.

Приведем несколько примеров.

Пример 1. Функция f (x) = С = const имеет предел в каж­дой точке числовой прямой. Действительно, любой последо­вательности (3.5), сходящейся к точке а, соответствует после­довательность (3.6), состоящая из одного и того же числа C, откуда следует, что f (x_n) С при n .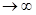

Пример 2. Функция f (x) = х в любой точке а числовой пря­мой имеет предел, равный а. Действительно, последователь­ности значений аргумента (3.5) и значений функции (3.6) в этом случае тождественны, и если последовательность { x_n } сходится к а, то и последовательность { f (x_n)} также сходится к а.

Пример 3. Функция f (x) = 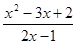имеет в точке x = 0 предел, равный -2. Действительно, пусть { x_n } — любая по­следовательность значений аргумента, сходящаяся к нулю, т.е. lim x_п = 0 при n 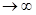, тогда в силу свойств последовательнос­тей 1—9 имеем

Левый и правый пределы функции

Здесь вводятся и в дальнейшем будут использоваться по­нятия односторонних пределов функции: когда последователь­ность значений аргумента x_n 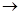а либо слева от точки а (левый предел), либо справа (правый предел), т.е. либо x_п < а, либо x_п > а. Для правого (левого) предела функции используется символическая запись:

Пример 4. Рассмотрим функцию f (x) = sign x (п. 3.1, при­мер 3). В точке x = 0 эта функция имеет левый и правый пределы:

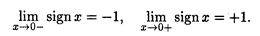
Действительно, для любой сходящейся к нулю последовательности { x_n }, у которой все элементы x_п < 0 (x_n > 0), соот­ветствующая последовательность значений функции состоит только из одного числа -1 (+1), т.е. предел слева (справа) в точке x = 0 также равен этому числу.

ТЕОРЕМА 1. Функция f(x) имеет в точке а предел тогда и только тогда, когда в этой точке существуют левый и правый пределы, причем они равны. В таком случае предел функции равен односторонним пределам.

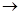
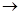Предел функции при х , x - , х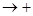

Кроме понятия предела функции в точке существует так­же и понятие предела функции при стремлении аргумента к бесконечности. Для обозначения предела функции при x 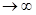используется запись: f (x) = А.

Приведем пример предела функции при х 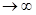. Пусть f (x) = 1/ x. Эта функция имеет предел при x 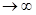, рав­ный нулю. Действительно, если (3.5) — бесконечно большая последовательность значений аргумента, то соответствующая последовательность (3.6) значений функции имеет вид 1/ x ₁, 1/ x ₂,..., 1/ x_n,...; она является бесконечно малой (п. 2.1), т. е. ее предел равен нулю, или в символической записи (1/ x) = 0.

Аналогично можно доказать, что (1/ xⁿ) = 0 при п > 0.

Дата добавления: 2014-10-15