Основные понятия теории

Определение 1. Дифференциальным уравнением второго по­рядка называется уравнение вида

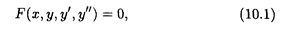
где х — независимая переменная, у — искомая функция, у' и у" — соответственно ее первая и вторая производные.

Примеры дифференциальных уравнений второго порядка:

Будем рассматривать уравнения, которые можно записать в виде, разрешенном относительно второй производной:

Как и в случае уравнения первого порядка, решением урав­нения (10.1) называется функция у = φ(x), определенная на некотором интервале (а, b), которая обращает это уравнение в тождество. График решения называется интегральной кривой. Имеет место теорема существования и единственности реше­ния уравнения второго порядка.

ТЕОРЕМА 1 (теорема Коши). Пусть функция f(x, у, у') и ее частные производные и 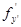, непрерывны в некоторой обла­сти D пространства переменных (x, у, у'). Тогда для любой внутренней точки М₀(х₀, у₀, у'₀) этой области существует единственное решение уравнения (10.2), удовлетворяющее ус­ловиям:

Геометрический смысл этой теоремы (ее доказательство мы не приводим) заключается в том, что через заданную точку (x ₀, y ₀) на координатной плоскости Оху проходит единствен­ная интегральная кривая с заданным угловым коэффициентом y ₀ ' касательной (рис. 10.1).

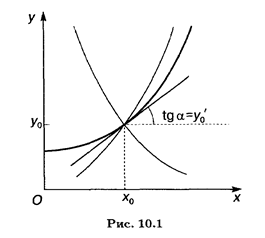
Условия (10.3) называются начальными условиями, а зада­чу отыскания решения уравнения (10.2) по заданным началь­ным условиям называют задачей Коши.

Общим решением уравнения (10.2) в некоторой области D называется функция у = φ(х, С ₁, С ₂), если она является реше­нием этого уравнения при любых постоянных величинах С ₁и C ₂, которые могут быть определены единственным образом при заданных начальных условиях (10.3). Частным решением уравнения (10.2) называется общее решение этого уравнения при фиксированных значениях постоянных С ₁ и C ₂: у = φ(х, С ₁⁰, С ₂⁰ ).

Рассмотрим для пояснения уравнение у" = 0. Его общее решение получается при двухкратном интегрировании этого уравнения:

где С ₁ и C ₂ — произвольные постоянные. Это решение пред ставляет собой семейство прямых, проходящих в произвольных направлениях, причем через каждую точку плоскости Охy проходит бесконечное число таких прямых. Поэтому для выделения частного решения, проходящего через заданную точку (х ₀, y ₀ ), следует задать еще и угловой коэффициент прямой, совпадающей в данном случае со своей касательной. Например, найдем частное решение, удовлетворяющее начальным условиям

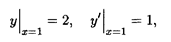
т.е. нужно найти прямую, проходящую через точку M (l, 2), с угловым коэффициентом, равным единице. Подстановка на­чальных условий в общее решение уравнения приводит к сис­теме двух линейных уравнений относительно постоянных С ₁и C ₂

откуда С ₁ = 1, C ₂ = 1. Таким образом, искомое частное реше­ние — это прямая у = х + 1.

Дата добавления: 2014-10-15