
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Тема 2.6. Основные теоремы линейного программирования
|
|
|
|
Определение. Линейная комбинация

точек  называется выпуклой, если
называется выпуклой, если
 > 0,
> 0, 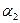 > 0,…,
> 0,…, 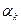 > 0 и
> 0 и  +
+ 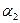 + …+
+ …+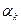 = 1.
= 1.
Определение. Множество точек называется выпуклым, если оно содержит любую выпуклую линейную комбинацию любых своих точек.
Теорема 1. Множество всех планов задачи ЛП является выпуклым множеством.
Доказательство. Пусть  – произвольные планы задачи ЛП. Это значит, что выполняются равенства:
– произвольные планы задачи ЛП. Это значит, что выполняются равенства:
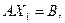
 …,
…,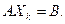
Пусть 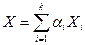 – выпуклая линейная комбинация взятых планов. Подставим в уравнение
– выпуклая линейная комбинация взятых планов. Подставим в уравнение  выражение
выражение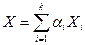 . Используя известные нам свойства линейных операций над матрицами, получаем:
. Используя известные нам свойства линейных операций над матрицами, получаем:
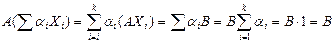 .
.
Таким образом,  является планом задачи ЛП. Теорема доказана.
является планом задачи ЛП. Теорема доказана.
Определение. Точка области называется вершиной (угловой точкой), если она не является выпуклой линейной комбинацией других точек.
Это определение не опирается на наглядность, но и не противоречит обыденному нашему представлению о вершине прямоугольника, треугольника, куба и т.п.
Теорема 2. Если оптимальный план задачи ЛП существует, то, по крайней мере, одна из вершин является оптимальным планом.
Доказательство. Обозначим через  оптимальный план. Будем считать, что
оптимальный план. Будем считать, что  – не вершина. Для конкретности рассуждений будем считать, что
– не вершина. Для конкретности рассуждений будем считать, что  – наибольшее значение целевой функции. Представим
– наибольшее значение целевой функции. Представим  в виде выпуклой линейной комбинации вершин
в виде выпуклой линейной комбинации вершин 
 , т.е.
, т.е.

 ,
,
где
 > 0,
> 0, 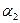 > 0,…,
> 0,…, 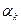 > 0 и
> 0 и  +
+ 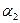 + …+
+ …+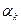 = 1.
= 1.
Тогда:
М = 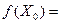

 )
)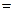
 =
=
=  .
.
Пусть 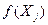 - наибольшее из чисел
- наибольшее из чисел
 .
.
Тогда:
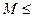
 =
=
( +
+ 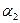 + …+
+ …+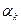 )
)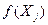 =
=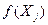 .
.
Отсюда следует, что 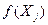 = М, то есть вершина
= М, то есть вершина 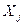 является оптимальным планом. Теорема доказана.
является оптимальным планом. Теорема доказана.
Теорема 3. Каждое невырожденное базисное решение системы ограничений задачи ЛП является вершиной.
Доказательство. Пусть 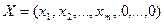 – невырожденное базисное решение системы ограничений (уравнений):
– невырожденное базисное решение системы ограничений (уравнений):  , где
, где
|
|
|
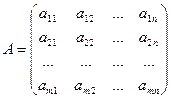 ,
, 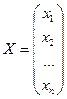 ,
,  .
.
Эту систему уравнений можно записать в виде:
 ,
,
где:  –
– 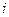 -й столбец матрицы
-й столбец матрицы  (
( .
.
Так как
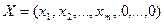 ,
,
то
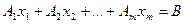 , (1)
, (1)
при этом векторы 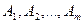 линейно независимые, коэффициенты
линейно независимые, коэффициенты 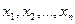 положительные.
положительные.
Допустим, что Х не является вершиной. Тогда  – выпуклая линейная комбинация k вершин (
– выпуклая линейная комбинация k вершин (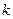 > 1). Очевидно, что все координаты этих вершин, начиная с (
> 1). Очевидно, что все координаты этих вершин, начиная с (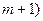 -й, равны нулю, ибо в противном случае, учитывая, что все
-й, равны нулю, ибо в противном случае, учитывая, что все 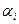 > 0 и что каждая координата точки Х является линейной комбинацией соответствующих координат этих вершин, точка X имела бы положительных координат больше m. Так как точка
> 0 и что каждая координата точки Х является линейной комбинацией соответствующих координат этих вершин, точка X имела бы положительных координат больше m. Так как точка
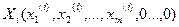
удовлетворяет системе ограничений, то справедливо равенство:
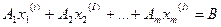 . (2)
. (2)
Вычтем из равенства (1) равенство (2). Получим равенство:
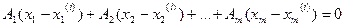 .
.
Но так как векторы 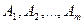 линейно независимые, то
линейно независимые, то
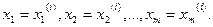
Таким образом, Х совпадает с вершиной Х . Теорема доказана.
. Теорема доказана.
Теорема 4. Каждая вершина области ограничений задачи ЛП является базисным решением ее системы ограничений.
Доказательство этой теоремы опускаем.
Тема 2.7. Метод последовательного улучшения плана (симплекс-метод)
Задача. Найти наибольшее значение функции f = 3 x  + 5 x
+ 5 x 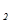 , если переменные величины x
, если переменные величины x  , x
, x 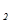 неотрицательные и удовлетворяют системе неравенств:
неотрицательные и удовлетворяют системе неравенств:

Решение. Вводим балансовые величины х 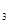 , х
, х  и в результате получаем систему ограничений в виде систем уравнений:
и в результате получаем систему ограничений в виде систем уравнений:
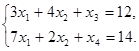
Балансовые переменные х 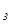 , x
, x 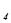 примем в качестве базисных, а переменные x
примем в качестве базисных, а переменные x  , х
, х 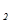 - в качестве свободных переменных. Выразим базисные переменные через свободные переменные:
- в качестве свободных переменных. Выразим базисные переменные через свободные переменные:
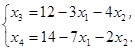
Целевую функцию f запишем в виде: f = 0 - (- З х  - 5 х
- 5 х 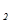 ). Приравняв свободные переменные к нулю, получим первое базисное решение (0;0;12;14). Ему соответствует значение
). Приравняв свободные переменные к нулю, получим первое базисное решение (0;0;12;14). Ему соответствует значение
f = 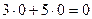 . Увеличение значения целевой функции
. Увеличение значения целевой функции
f = 0- (-3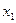 - 5
- 5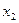 ) можно получить путем увеличения либо
) можно получить путем увеличения либо 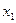 , либо
, либо 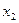 . Целесообразнее оставить
. Целесообразнее оставить 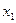 равным нулю, а увеличить
равным нулю, а увеличить 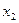 ибо модуль коэффициента при
ибо модуль коэффициента при 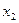 больше модуля коэффициента при
больше модуля коэффициента при 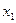 . Увеличить
. Увеличить 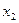 можно до тех пор, пока переменные
можно до тех пор, пока переменные  остаются неотрицательными, т.е.:
остаются неотрицательными, т.е.:
|
|
|

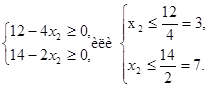
Положим, что:
 .
.
Тогда 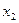 = 3,
= 3, 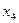 = 8. Получим второе базисное решение (0;3;0;8). Теперь
= 8. Получим второе базисное решение (0;3;0;8). Теперь 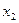 ,
, 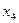 -базисные переменные,
-базисные переменные, 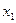 ,
, 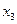 - свободные переменные. Второму базисному решению соответствует значение целевой функции
- свободные переменные. Второму базисному решению соответствует значение целевой функции
f = 3 0
0  = 15.
= 15.
Выразим базисные переменные х2, x 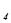 и целевую функцию через свободные переменные х
и целевую функцию через свободные переменные х  , х3.
, х3.
4 x 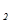 = 12 - 3 x
= 12 - 3 x  - х3, x
- х3, x 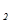 = 3-
= 3-
x 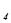 = 14-7 x 1 - 2
= 14-7 x 1 - 2
f = 3 x  + 5 x
+ 5 x 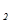 = 3 x
= 3 x  +5
+5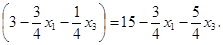
Итак, имеем:
f = 15 - 

Видим, что увеличение x  или х 3 с нулевого значения повлечет только уменьшение достигнутого ранее значения целевой функции. Таким образом, f max = 15 и (0;3) – оптимальный план (значение балансовых переменных опускаем).
или х 3 с нулевого значения повлечет только уменьшение достигнутого ранее значения целевой функции. Таким образом, f max = 15 и (0;3) – оптимальный план (значение балансовых переменных опускаем).
Теперь сформулируем алгоритм симплекс- метода.
I шаг. Приводим систему ограничений к виду:
x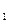 =
=  - (a
- (a xm+1 +a
xm+1 +a  m+2xm+2 +...+ a
m+2xm+2 +...+ a  nxn),
nxn),
х2 = 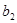 - (а2
- (а2 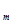 +
+  x
x 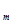
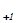 + а2
+ а2 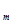
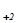 x m+2 +...+а2 n х n),
x m+2 +...+а2 n х n),
….........................................................................
хm =  - (a
- (a 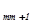 x
x 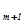 +a
+a  x
x 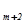 +
+  +a
+a 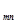 x
x  ),
),
где x  , x2,..., x m - базисные переменные, x
, x2,..., x m - базисные переменные, x 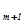 ,
,  ,x
,x  - свободные переменные,
- свободные переменные, 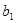
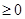 ,
, 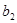
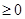 ,...,
,..., 
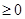 .
.
II шаг. Полагая свободные переменные равными нулю, получаем первое базисное решение
( 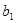 ,
, 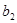 ,...,
,..., 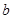
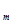 ,0,...,0). Находим также первое значение целевой функции, т.е. значение
,0,...,0). Находим также первое значение целевой функции, т.е. значение
f ( 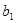 ,
, 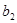 ,...,
,..., 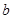
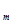 ,0,...,0) = f
,0,...,0) = f  .
.
III шаг. Выражаем целевую функцию f через свободные переменные:
f = f  - (
- ( m+1 xm+1 +
m+1 xm+1 +  m+2 xm+2+...+
m+2 xm+2+...+ 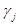
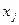 +...+
+...+  nxn).
nxn).
Если среди коэффициентов  m+1,...,
m+1,...,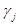 ,...,
,..., n нет отрицательных,
n нет отрицательных,
то f = fmax и (
= fmax и ( 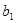 ,
, 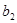 ,...,
,..., 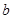
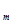 ,0,...,0) – оптимальный план, и задача решена.
,0,...,0) – оптимальный план, и задача решена.
Допустим, что среди чисел  m+1,…
m+1,…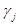 ,…,
,…, n имеются отрицательные, например,
n имеются отрицательные, например, 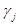 . Если при этом среди коэффициентов
. Если при этом среди коэффициентов 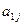 ,
, ,...,
,..., нет положительных, то х
нет положительных, то х 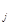 можно увеличивать неограниченно (переменные x
можно увеличивать неограниченно (переменные x  , x2,..., х m не станут от этого отрицательными) и, следовательно, fmax = +
, x2,..., х m не станут от этого отрицательными) и, следовательно, fmax = +
Пусть 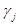 < 0, но среди коэффициентов а
< 0, но среди коэффициентов а , a
, a ,...,a
,...,a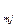 есть положительные. Без потери общности будем считать, что
есть положительные. Без потери общности будем считать, что
a >0, a
>0, a >0,..., a
>0,..., a >0.
>0.
Если
min 

то переменную х  выводим из состава базисных переменных, полагая x
выводим из состава базисных переменных, полагая x  = 0, а переменную
= 0, а переменную 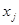 вводим в состав базисных переменных, полагая
вводим в состав базисных переменных, полагая 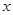
 =
=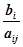 . Таким образом, приходим к новым базисным переменным и новым свободным переменным. Разрешаем систему ограничений относительно новых базисных переменных и переходим снова к шагу II.
. Таким образом, приходим к новым базисным переменным и новым свободным переменным. Разрешаем систему ограничений относительно новых базисных переменных и переходим снова к шагу II.
Таким образом, если оптимальное решение задачи ЛП существует, то симплекс-метод позволяет через конечное число шагов найти его среди базисных решений системы ограничений. В принципе, оптимальный план можно найти простым перебором всех базисных решений, если их не так много.
|
|
|
|
|
|
|
|
Дата добавления: 2014-10-31; Просмотров: 998; Нарушение авторских прав?; Мы поможем в написании вашей работы!