Загальна математична модель лінійного програмування

ГРАФІЧНИЙ МЕТОД РОЗВ’ЯЗУВАННЯ ЗАДАЧ ЛІНІЙНОГО ПРОГРАМУВАННЯ

ОСНОВНІ АНАЛІТИЧНІ ВЛАСТИВОСТІ РОЗВ’ЯЗКІВ ЗАДАЧ ЛІНІЙНОГО ПРОГРАМУВАННЯ

ГЕОМЕТРИЧНА ІНТЕРПРЕТАЦІЯ ЗЛП

Загальна лінійна математична модель економічних процесів і явищ — так звана загальна задача лінійного програмування (ЛП) подається у вигляді:

знайти максимум (мінімум) функції (1)

або

за умов

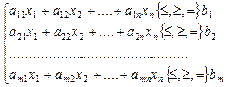(2)

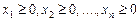. (3)

Отже, потрібно знайти значення змінних x ₁, x ₂, …, x_n, які задовольняють умови (2) і (3), тоді як цільова функція набуває екстремального (максимального чи мінімального) значення.

Задачу (1)—(3) легко звести до канонічної форми, тобто до такого вигляду, коли в системі обмежень (2) всі b_і (і = 1, 2, …, n) невід’ємні, а всі обмеження є рівностями.

Якщо якесь b_і від’ємне, то, помноживши і -те обмеження на (–1), дістанемо у правій частині відповідної рівності додатне значення. Коли і -те обмеження має вигляд нерівності , то останню завжди можна звести до рівності, увівши допоміжну змінну x_{n + 1}: .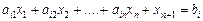

Аналогічно обмеження виду зводимо до рівності, віднімаючи від лівої частини допоміжну змінну х_{n + 2}, тобто

Приклад 1.

Записати в канонічній формі таку задачу ЛП:

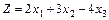® max

за умов

.

Розв’язування. Помножимо другу нерівність на (–1) і введемо відповідно допоміжні змінні х ₄ і х ₅ для другого та третього обмеження:

Неважко переконатися, що допоміжні змінні, у цьому разі х ₄ і х ₅, є невід’ємними, причому їх уведення не змінює цільової функції.

Отже, будь-яку задачу ЛП можна записати в такій канонічній формі:

знайти максимум функції 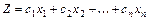® max (2.4)

за умов

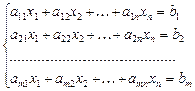(5)

. (6)

Задачу (2.4)—(2.6) можна розв’язувати на мінімум, якщо цільову функцію помножити на (–1), тобто

.

Дата добавления: 2014-10-31