Обратное преобразование Лапласа

Обратным преобразованием Лапласа называется определение временной функции f (t), для которой прямое преобразование Лапласа

.

Обратным Z -преобразованием или 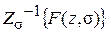называется определение дискретной функции времени f (nT) (f [(n + s) T ]), для которой или .

Отметим ограничения, которые следует иметь в виду, выполняя обратное преобразование Лапласа или обратное Z -преобразование.

1. Не каждая функция F (s) имеет обратное преобразование. Существование обратного преобразования определяется необходимыми и достаточными условиями, накладываемыми на F (s).

2. Прямое преобразование Лапласа единственно для каждой f (t), имеющей такое преобразование. Обратное утверждение, в общем случае, несправедливо. Различные разрывные функции могут иметь одинаковое преобразование Лапласа. Например, единичная ступенчатая функция f (t) = = 0 для t < 0 и f (t) = 1 для t > 0 имеет преобразование Лапласа 1/ s независимо от значения, принимаемого при t = 0.

3. Обратное Z – или Z _s - преобразование, если оно существует, позволяет определить лишь последовательность отдельных значений непрерывной функции-оригинала, существующих в моменты времени t = nT или
t = (n + s)T. Одной и той же последовательности дискретных значений f (тT) или f [(n + s)T] может соответствовать множество огибающих f (t). Поэтому по обратному Z – преобразованию принципиально невозможно восстановить непрерывную функцию f (t).

Существует два общих практических способа определения обратных преобразований как для непрерывных, так и для дискретных систем.

1. Использование таблиц обратных преобразований Лапласа и обратных Z –преобразований, например в [6]. Если исходного F (s) и F (z) изображения нет в таблице следует использовать разложение его на сумму или произведение изображений, имеющихся в таблице.

2. Использование формулы обращения.

Для непрерывного изображения

.

Значение контурного интеграла определяется в открытом интервале, где f (t) ограничена и имеет конечное число точек экстремума и разрыва. Решение часто удается получить при помощи теоремы о вычетах:

,

где z ₁, z ₂, …, z_n особые точки .

Вычисление интеграла обращения как суммы вычетов широко используется в различных программных продуктах, используемых при компьютерном моделировании систем автоматического управления.

Для дискретного изображения формула обращения имеет вид

.

Контур интегрирования R должен охватывать начало координат плоскости Z и все особые точки подынтегральной функции. Как и в непрерывном случае, круговой интеграл обычно рассчитывается как сумма вычетов подынтегральной функции в особых точках:

.

N – число вычетов; N = q + 1 для n = q для n > 0, где q – число особых точек функции F (z,s).

Вычеты вычисляются следующим образом:

- для простого полюса

;

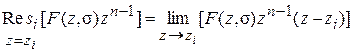- для кратного полюса кратности m

.

Кроме двух общих методов, в случае обратного Z –преобразования используется также разложение F (z,s) в ряд по возрастающим степеням z ^-1 в соответствии с основной формулой Z –преобразования

.

Когда F (z,s) представлено рациональной дробью разложение по степеням z ^-1 может быть выполнено простым делением числителя на знаменатель.

Пример. Пусть .

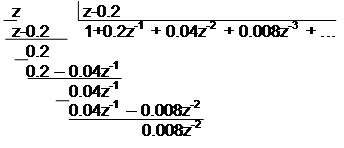Получаем f (n) = 1 0.2 0.04 0.008.

При более сложных выражениях F (z) и F (z,s) лучше использовать вычисление по рекуррентной формуле:

.

Здесь b ₀, …, b_k, …, b_p – коэффициенты числителя F (z,s) a ₀, …, a_i, …, a_q – коэффициенты знаменателя F (z,s). При q = p формулы значительно упрощаются

Аналогично преобразованию дифференциального уравнения непрерывной системы осуществляется Z -преобразование разностного уравнения дискретной системы.

Пусть дискретная система описывается уравнением

Подвергнем это разностное уравнение Z -преобразованию, принимая начальные условия нулевыми:

Записывая полученное уравнение в сжатой форме, получим

Беря отношения Z -изображений, получим передаточные функции дискретной системы по управляющему и возмущающему воздействиям:

.

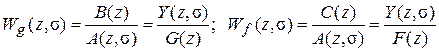Для дискретно-непрерывной системы определение дискретной передаточной функции выполняется на основе перехода от непрерывной передаточной функции приведенной непрерывной части к ее дискретному эквиваленту в Z -области. Покажем этот переход на примере разомкнутой дискретно-непрерывной системы с одним импульсным элементом на ее входе (рис. 5.7). На схеме .

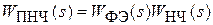Так как входной сигнал приведенной непрерывной части представляет собой сумму модулированных по площади входным сигналом g (t) d-функций, выходной сигнал y (t) будет представлять сумму реакции ПНЧ на d-функции; т. е. сумму функций веса ПНЧ

Если вместо непрерывного сигнала y (t)отмечать лишь его дискретные значения y (nT) или y [(n + s) T ], то получим решетчатую функцию y (n) или y (n, s):

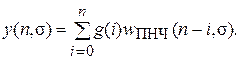
Подвергнем эту решетчатую функцию модифицированному Z -преобразованию

С учетом теоремы свертки имеем

Таким образом

.

Здесь - дискретная передаточная функция разомкнутой дискретно-непрерывной системы. С одной стороны, она связывает Z -изображения дискретных сигналов, с другой стороны, она определяется как Z -форма передаточной функции приведенной непрерывной части.

Дата добавления: 2014-10-31