Распределение ресурсов

Модель развития экономики (модель Харрода)

Основная производственная задача Л. В. Канторовича

Однопродуктовая модель

Однопродуктовая модель предназначена для оптимизации распределения объемов производства по способам производства. Постановка задачи может выполняться с различными экономическими оценками.

Определяемые величины обозначим через x (i) – величина планируемого производства продукции по i – му способу производства.

Основное ограничение предусматривает необходимость выполнения общего плана производства:

x (1) + x (2) +… + x (n) = V.

Здесь n – число способов производства, V – общий план производства. Каждая из величин x (i) должна быть больше нулялибо равна нулю:

x (i) > 0.

Оптимизационная оценка вариантов решения задачи имеет вид

f(x (1)) + f(x (2)) +… + f(x (n)).

Способ решения задачи зависит от вида функции f. При линейной функции методом решения будет линейное программирование, при нелинейной функции – возможно привлечение метода множителей Лагранжа либо динамического программирования.

Одна из первых математических моделей была разработана в 1939 г. Л. В. Канторовичем. Пусть имеется некий производственный процесс, предназначенный для выпуска n видов продукции. По каждому из видов продукции заданы ограничения на объем выпуска и нормы расхода привлекаемых ресурсов. Поставка продукции потребителю осуществляется комплектами, и поэтому требуется сформировать плановый ассортимент выпуска продукции, обеспечивающий максимальное число комплектов поставки продукции.

Формализуя математическую постановку задачи, введем следующие ограничения:

x(i) > 0;

a(s,1)x(1) + a(s,2)x(2) +… + a(s,n)x(n) ‹V(s).

Оптимизационная оценка имеет вид

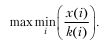
Здесь k(i) – количество единиц i – го продукта в комплекте. Решается задача методом линейного программирования, который фактически и появился как алгоритм решения этой математической задачи в 1939 г.

Одна из первых упрощенных моделей развития экономики страны была предложена английским экономистом Р. Харродом. В модели учитывается один определяемый фактор – капитальные вложения, а состояние экономики оценивается через размер национального дохода.

Для математической постановки задачи введем следующие обозначения:

y (t) – национальный доход в год t;

k (t) – производственные фонды в год t;

c (t) – объем потребления в год t;

s (t) – объем накопления в год t;

ν (t) – капитальные вложения в год t.

Будем предполагать, что функционирование экономики происходит при выполнении следующих условий:

y (t) = c (t) + s (t) – условие баланса доходов и расходов за каждый год;

s (t) = v (t) – условие исключения пролеживания капитала;

s (t) = ay (t) – условие пропорционального деления национального годового дохода.

Два условия принимаются для характеристики внутренних экономических процессов. Первое условие характеризует связь капитальных вложений и общей суммы производственных фондов, второе – связь национального годового дохода и производственных фондов. Капитальные вложения в год t могут рассматриваться как прирост производственных фондов или производная от функции, «производственные фонды» принимаются как капитальные годовые вложения:

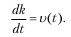
Национальный доход в каждый год принимается как отдача производственных фондов с соответствующим нормативным коэффициентом фондоотдачи:

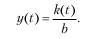
Соединяя условия задачи, можно получить следующее соотношение:

Отсюда следует итоговое уравнение Харрода:

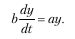
Его решением является экспоненциальное изменение национального дохода по годовым интервалам:

Несмотря на упрощенный вид математической модели, ее результат может быть использован для укрупненного анализа национальной экономики. Параметры a и b могут стать параметрами управления при выборе плановой стратегии развития с целью максимального приближения к предпочтительной траектории изменения национального дохода или для выбора минимального интервала времени достижения заданного уровня национального дохода.

Пусть имеется m видов ресурсов, каждый i – й ресурс в количестве b_i(i = 1… m). Эти ресурсы нужно использовать для n видов продукции. Для выпуска единицы j – го вида продукции необходимо a_ij единиц i – го вида ресурса. Требуется определить, сколько каждого вида продукции следует произвести, чтобы такой выпуск был наилучшим для принятого критерия оптимальности.

В реальных задачах суммарное количество основных x_j(j = 1… n) и дополнительных y_i (i = 1… m) переменных всегда больше, чем число зависимостей m, поэтому система (1) ограничений имеет бесчисленное множество решений. Из этого бесчисленного множества следует выбрать одно – оптимальное, соответствующее критерию – цели решения задачи.

Цель задачи распределения ресурсов определяется какой‑либо одной из двух взаимоисключающих постановок:

1. При заданных ресурсах максимизировать получаемый результат.

2. При заданном результате минимизировать потребные ресурсы.

Первая постановка аналитически будет сформулирована следующим образом:

где x_j – количество выпускаемой продукции j – го вида – искомая переменная (j = = 1… n); n – количество наименований продукции; с. – величина, показывающая, какой вклад в результат дает единица продукции j – го вида; b_i – заданное количество ресурса i – го вида (i = 1… m); m – количество наименований ресурсов; a_ij – норма расхода ресурса, т. е. количество ресурса i – го вида, потребляемого на производство единицы j – го вида продукции.

Решение задачи (1) дает нахождение таких значений x_j, которые обеспечивают при заданных ресурсах получение максимального результата.

Вторая постановка задачи будет иметь вид:

где C – минимально допустимое значение потребного результата.

Совместимость ограничивающих условий В общую постановку задачи оптимизации входят неравенства вида

где n – число неизвестных; m – число неравенств.

Если в каждое неравенство добавить неотрицательное неизвестное y ≥ 0 (i = 1… m), то от системы неравенств можно перейти к системе уравнений

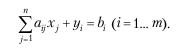
В этой системе общее число неизвестных N = n + m, где n – число основных неизвестных x_j; m – число дополнительных неизвестных y_i, которое равно числу уравнений.

Возможны три варианта соотношения величин N и m.

1. Число неизвестных меньше, чем число уравнений: N < m. Например, N = 1, m = 2.

Очевидно, эта система решения не имеет, т. е. нет таких значений x 1, которые бы удовлетворяли обоим уравнениям. В этом случае говорят, что система условий несовместна. Значит, если число неизвестных N меньше числа уравнений m, то система решения не имеет и является несовместной.

2. Число неизвестных равно числу уравнений: N = m.

Например, нетрудно вычислить, что решением этой системы будут значения x₁ = 2, x₂ = 1. Таким образом, линейная система, в которой число неизвестных N равно числу уравнений m, имеет одно решение.

3. Число неизвестных больше числа уравнений: N > m.

Например, 2x₁ + x₂ = 2. Очевидно, что все значения x₁ и x₂, лежащие на прямой этого уравнения, являются его решением. Если в системе число неизвестных N больше числа уравнений m, то такая система имеет бесчисленное множество решений.

Дата добавления: 2014-11-20