
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пределы и непрерывность
|
|
|
|
Рекомендации по решению типовых задач по дифференциальному исчислению
Число  называется пределом числовой последовательности
называется пределом числовой последовательности 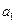 ,
, 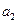 ,…,
,…, 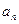 ,…, если для любого, даже сколь угодно малого положительного числа
,…, если для любого, даже сколь угодно малого положительного числа 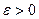 , найдется такой номер
, найдется такой номер 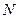 (зависящий от
(зависящий от 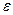 ,
, 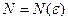 ), что для всех членов последовательности с номерами
), что для всех членов последовательности с номерами 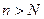 верно неравенство:
верно неравенство: 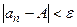 .
.
Предел числовой последовательности обозначается 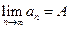 или
или 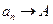 при
при 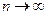 . Последовательность, имеющая предел, называется сходящийся, в противном случае – расходящейся.
. Последовательность, имеющая предел, называется сходящийся, в противном случае – расходящейся.
Число  называется пределом функции
называется пределом функции 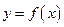 при
при 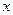 , стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа
, стремящемся к бесконечности, если для любого, даже сколь угодно малого положительного числа 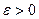 , найдется такое положительное число
, найдется такое положительное число 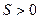 (зависящее от
(зависящее от 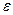 ;
; 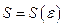 ), что для всех
), что для всех 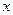 таких, что
таких, что 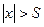 , верно неравенство:
, верно неравенство: 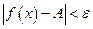 .
.
Число  называется пределом функции
называется пределом функции 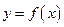 при
при 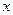 , стремящемся к
, стремящемся к 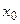 (или в точке
(или в точке 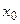 ), если для любого, даже сколь угодно малого положительного числа
), если для любого, даже сколь угодно малого положительного числа 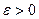 , найдется такое положительное число
, найдется такое положительное число 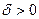 (зависящее от
(зависящее от 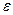 ;
; 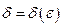 ), что для всех
), что для всех 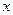 , не равных
, не равных 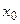 и удовлетворяющих условию
и удовлетворяющих условию 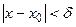 , выполняется неравенство:
, выполняется неравенство: 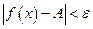 .
.
Теоремы о пределах:
1. Предел алгебраической суммы конечного числа функций равен такой же сумме пределов этих функций, т.е. 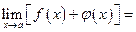
 .
.
2. Предел произведений конечного числа функций равен произведению пределов этих функций, т.е. 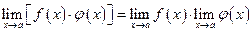 .
.
3. Предел частного двух функций равен частному пределов этих функций (при условии, что предел делителя не равен нулю), т.е. 
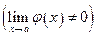 .
.
Первым замечательным пределом называется 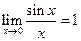 , вторым замечательным пределом
, вторым замечательным пределом 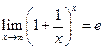 .
.
Пример 7.1. Найти следующие пределы: а) 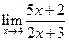 , б)
, б) 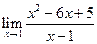 , в)
, в) 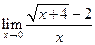 , г)
, г) 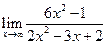 .
.
Решение.
а) Так как 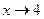 , то числитель дроби стремиться к числу
, то числитель дроби стремиться к числу 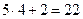 , а знаменатель – к числу
, а знаменатель – к числу 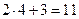 . Следовательно,
. Следовательно, 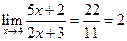 .
.
б) Числитель и знаменатель дроби при 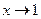 стремиться к нулю (неопределенность вида
стремиться к нулю (неопределенность вида 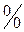 ). Разложим на множители числитель дроби:
). Разложим на множители числитель дроби:  .
.
|
|
|
в) Умножим числитель и знаменатель дроби на сумму 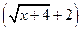 :
: 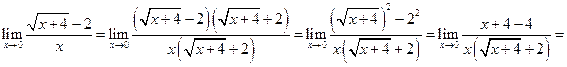
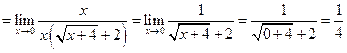 .
.
г) Числитель и знаменатель дроби неограниченно возрастают при 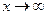 . В таком случае говорят, что имеет место неопределенность вида
. В таком случае говорят, что имеет место неопределенность вида 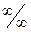 . Разделив на
. Разделив на 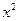 числитель и знаменатель дроби, получаем
числитель и знаменатель дроби, получаем 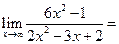
 , так как при
, так как при 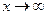 каждая из дробей
каждая из дробей 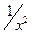 ,
,  ,
, 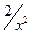 стремиться к нулю.
стремиться к нулю.
Пример 7.2. Используя первый замечательный предел вычислить: а) 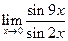 , б)
, б) 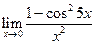 .
.
Решение.
а) Используя первый замечательный предел, имеем: 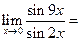
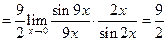 .
.
б) 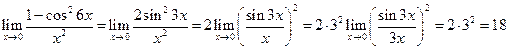 .
.
Пример 7.3. Используя второй замечательный предел вычислить 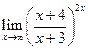 .
.
Решение. 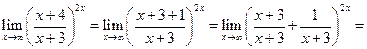
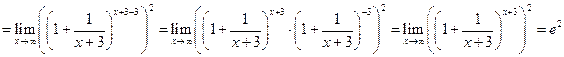 .
.
Функция 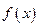 называется непрерывной в точке
называется непрерывной в точке 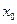 , если она удовлетворяет следующим трем условиям: 1) определена в точке
, если она удовлетворяет следующим трем условиям: 1) определена в точке 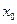 (т.е. существует
(т.е. существует 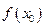 ); 2) имеет конечный предел функции при
); 2) имеет конечный предел функции при 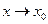 ; 3) этот предел равен значению функции в точке
; 3) этот предел равен значению функции в точке 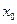 , т.е.
, т.е. 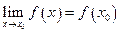 .
.
Пример 7.4. Для каждой из заданных функций найти точки разрыва и исследовать их характер: а) 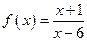 , б)
, б) 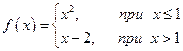 .
.
Решение.
а) Функция 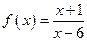 не определена в точке
не определена в точке 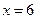 и, следовательно, в этой точке функция терпит разрыв. Найдем односторонние пределы:
и, следовательно, в этой точке функция терпит разрыв. Найдем односторонние пределы: 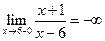 ,
, 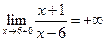 . Так как односторонние пределы равны бесконечности, значит, точка
. Так как односторонние пределы равны бесконечности, значит, точка 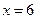 – точка разрыва 2-го рода, точка бесконечного разрыва.
– точка разрыва 2-го рода, точка бесконечного разрыва.
б) Функция 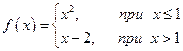 в точке
в точке  не является непрерывной – первое условие непрерывности выполнено – существует
не является непрерывной – первое условие непрерывности выполнено – существует 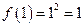 , но нарушено второе условие отсутствует
, но нарушено второе условие отсутствует 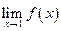 (точнее говоря, здесь существуют односторонние пределы функции слева
(точнее говоря, здесь существуют односторонние пределы функции слева 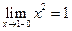 и справа
и справа 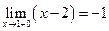 , но общего предела при
, но общего предела при 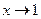 не существует).
не существует).
|
|
|
|
|
Дата добавления: 2014-11-25; Просмотров: 693; Нарушение авторских прав?; Мы поможем в написании вашей работы!