Лекция № 51. Тема 1: Определение кратного интеграла

КРАТНЫЕ ИНТЕГРАЛЫ

1.1. Задачи, приводящие к понятию кратного интеграла

Задача 1. Определение массы тела.

Рассмотрим тело, которое занимает пространственную область 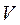, с плотностью 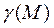, где точка 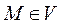. Найдём его массу. Если 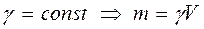. В нашем случае разобьём тело на части с объёмами: . Внутри каждой части произвольно выберем точку 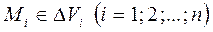и определим значение 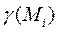. Если части разбиения достаточно малы, то , а вся масса

. (1)

При этом, чем меньше , тем равенство (1) точнее. Если ввести понятие диаметра области 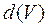- наибольшее расстояние между двумя точками её границы, то из формулы (1) путём предельного перехода получим точное значение массы тела

.

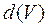Например, если область является круг, то - диаметр этого круга; если - прямоугольный параллелепипед, то 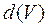- его диагональ.

Задача 2. Определение заряда тела.

Рассуждая аналогично, можно показать, что если в теле распределен заряд плотностью , то суммарная величина заряда вычисляется по формуле

.

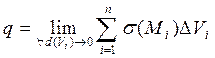1.2. Определение кратного интеграла и его основные свойства

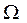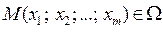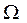Пусть в пространстве любого числа измерений т задана область , в каждой точке которой определена функция . Разобьём область на п подобластей с мерами (длина, площадь, объём и т.д.): . Внутри каждой из них произвольно выберем точки: и составим сумму вида

(2)

которая называется интегральной суммой для функции по области .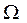

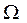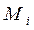Определение 1. Если существует предел интегральной суммы (2) и он не зависит от способа разбиения области на подобласти и выбора точек , то значение этого предела называется кратным интегралом от функции по области 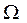и обозначается

Замечание 1. Легко проверить, что определение определённого интеграла является частным случаем кратного интеграла, если в качестве области 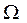рассмотреть отрезок числовой оси, на котором задана функция одной переменной. Из этого факта следует:

Теорема существования кратного интеграла. Если непрерывна в замкнутой области 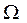, то она интегрируема в этой области.

Основные свойства кратных интегралов:

1. Свойство линейности. Если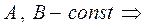

.

2. Свойство аддитивности. Есл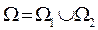и и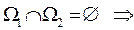

.

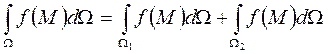3. - мера области.

4. Если .

Отсюда, если 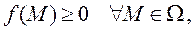то

5. Теорема об оценке интеграла.

Если .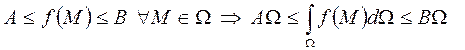

6. Теорема о среднем значении.

Существует такая точка 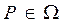, для которой выполняется

.

Дата добавления: 2014-11-16