
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция № 69. Определение функции комплексной переменной
|
|
|
|
ТЕОРИЯ ФУНКЦИЙ КОМПЛЕКСНОЙ ПЕРЕМЕННОЙ
1.1. Комплексные числа и действия над ними
Вначале введём понятие комплексного числа.
Определение 1. Комплексным числом называется выражение 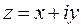 , где х и у действительные числа, а
, где х и у действительные числа, а  - мнимая единица.
- мнимая единица.
Такая форма представления комплексного числа называется алгеб-раической формой записи комплексного числа, при этом используются обозначения: 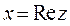 - действительная часть комплексного числа,
- действительная часть комплексного числа,  - мнимая часть комплексного числа.
- мнимая часть комплексного числа.
Из этого определения следуют правила действия над комплексными числами:
Если  и
и 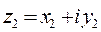 , то
, то
 , если
, если 


Определение 2. Комплексные числа 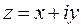 и
и  называются комплексно сопряженными.
называются комплексно сопряженными.
Легко показать, что  .
.
Тогда 
Пример 1. 
1.2. Тригонометрическая и показательная формы записи
комплексного числа
 Между комплексными числами
Между комплексными числами 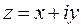 и точками
и точками 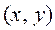 на плоскости можно установить взаимнооднозначное соответствие. В этом случае плоскость
на плоскости можно установить взаимнооднозначное соответствие. В этом случае плоскость  называется комплексной плоскостью, координат-ные оси - соответственно действительной осью и мнимой осью.
называется комплексной плоскостью, координат-ные оси - соответственно действительной осью и мнимой осью.
Тогда каждому комплексному
числу 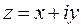 ставится в у
ставится в у 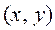
соответствие точка 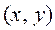
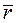
или её радиус-вектор  .
. 
О х
При этом полярные координаты 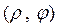 точки, изображающей комп-лексное число, называются соответственно модулем и аргументом комп-лексного числа и обозначаются
точки, изображающей комп-лексное число, называются соответственно модулем и аргументом комп-лексного числа и обозначаются  и
и  .
.
Так как  , то получим тригонометрическую форму записи комплексного числа
, то получим тригонометрическую форму записи комплексного числа
 (1)
(1)
Очевидно, если 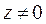 , то аргумент имеет бесконечно много значений, получаемых по формуле
, то аргумент имеет бесконечно много значений, получаемых по формуле 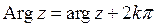 , где
, где  называют главным значением аргумента и по определению полагают
называют главным значением аргумента и по определению полагают  . Два комплексных числа будут равны, если
. Два комплексных числа будут равны, если  и
и  .
.
Если воспользоваться формулой Эйлера  , то фор-мула (1) примет вид (показательная форма записи комплексного числа)
, то фор-мула (1) примет вид (показательная форма записи комплексного числа)
|
|
|
 (2)
(2)
Такие формы представления комплексных чисел очень удобны для действий над ними. Так непосредственно можно проверить следующие правила:
 (3)
(3)
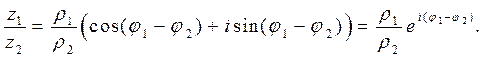 (4)
(4)
Из формулы (3) умножения комплексных чисел следует правило возведения в степень
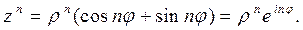 (5)
(5)
Из правила (5) с учетом определения корня п -ой степени из числа z получаем 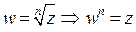 и, если
и, если 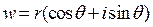 , а
, а  , то будут справедливы равенства
, то будут справедливы равенства 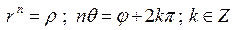 , из которых следуют соотношения
, из которых следуют соотношения  .
.
Таким образом, приходим к правилу извлечения корней из комплекс-ных чисел
 , (6)
, (6)
где, для того чтобы эти значения были различными, должно  .
.
Пример 2. Найти  .
.
Представим число i в тригонометрической форме (1)
 .
.
Тогда по формуле (6) получаем два различных корня:

 .
.
Путем возведения полученных корней в квадрат легко убедится в правильности полученного результата.
1.3. Определение функции комплексной переменной
Определение 3. Множество точек комплексной плоскости, которые удовлетворяют неравенству  , называется
, называется  -окрестностью точки
-окрестностью точки 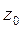 .
.
Геометрически оно представляет собой круг радиуса  с центром в точке
с центром в точке 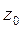 , так как
, так как
 .
.
Определение 4. Множество D точек комплексной плоскости называ-ется областью, если:
1. Каждая точка принадлежит D с некоторой окрестностью (свойство открытости);
2. Любые две точки, принадлежащие D, можно соединить непрерывной линией, все точки которой принадлежат D (свойство связности).
Определение 5. Область D с присоединенной границей называется замкнутой областью и обозначается  .
.
Например,  - замкнутая область (круг).
- замкнутая область (круг).
Определение 6. Область D называется односвязной, если любая замк-нутая кривая, полностью принадлежащая области, может быть стянута в точку с помощью деформации без выведения из границ области.

y


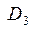
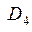
x
Здесь область  - односвязная, а области
- односвязная, а области  ,
, 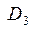 и
и 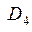 - много-связные.
- много-связные.
Определение 7. В области D определена функция комплексной пере-менной  , если каждой точке
, если каждой точке  по определённому правилу или закону поставлены в соответствие одна или несколько точек
по определённому правилу или закону поставлены в соответствие одна или несколько точек  .
.
|
|
|
Геометрически это выглядит так

y v
D  w
w
z  G
G
O x O и
В первом случае функция называется однозначной, а во втором – многозначной.
Если  , а
, а  , то для определения w достаточно задать две функции
, то для определения w достаточно задать две функции  и
и  .
.
 Определение 8. Функция
Определение 8. Функция  , ставящая в соответствие точке
, ставящая в соответствие точке  одну или несколько точек
одну или несколько точек  , называется обратной функцией к функции
, называется обратной функцией к функции  .
.
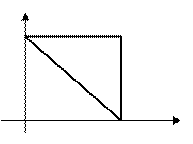
Пример 3. Рассмотрим функцию у
 , заданную в области D:
, заданную в области D:  D
D
Найти область G, в которую данная О 1 х
функция преобразует область D.
В этом случае

Подставим в эту систему уравнение 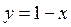 границы области D (гипотенуза треугольника) и тогда
границы области D (гипотенуза треугольника) и тогда 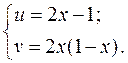
Получили параметрические уравнения линии (часть границы области G). Если исключить параметр х, то уравнение первой части границы области G примет вид 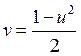 .
.
Подставим в систему уравнение 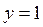 границы области D (катет треугольника):
границы области D (катет треугольника): 
И, наконец, аналогично поступим со следующей границей 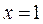 области D:
области D:

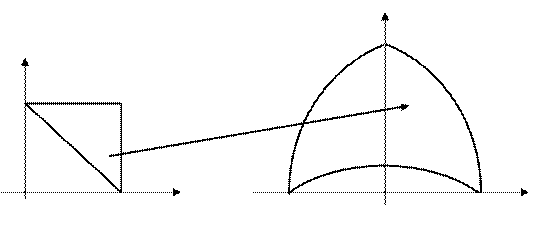
Изобразим все полученные границы области G на рисунке.
v
y
1 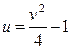
 w
w 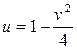
z 
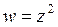 G
G 
O 1 x -1 O 1 u
Таким образом, данная функция отображает прямоугольный треуголь-ник D на криволинейный треугольник G.
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 584; Нарушение авторских прав?; Мы поможем в написании вашей работы!