
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решаем четыре системы сравнений 8 страница
|
|
|
|
Пример 7. 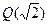 – простое алгебраическое расширение поля
– простое алгебраическое расширение поля  .
.
Пример 8. 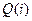 – поле гауссовых чисел – простое алгебраическое расширение поля
– поле гауссовых чисел – простое алгебраическое расширение поля  .
.
Пример 9. 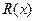 – простое трансцендентное расширение поля
– простое трансцендентное расширение поля  . Это поле рациональных функций над полем
. Это поле рациональных функций над полем  .
.
Определение 23. Пусть 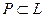 – башня полей. Расширение
– башня полей. Расширение  поля
поля  называется конечным расширением, если существует система элементов в
называется конечным расширением, если существует система элементов в 
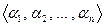 такая, что любой элемент
такая, что любой элемент 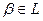 представляется однозначно в виде
представляется однозначно в виде 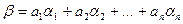 , где
, где  .
.
Легко видеть, что в этом случае поле  есть конечномерное линейное пространство над полем
есть конечномерное линейное пространство над полем  . Система элементов
. Система элементов 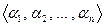 есть базис этого пространства.
есть базис этого пространства.
Определение 24. Размерность конечного расширения  поля
поля  как линейного пространства над
как линейного пространства над  называется степенью поля
называется степенью поля  над полем
над полем  и обозначается
и обозначается 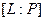 , а его базис называется базисом поля
, а его базис называется базисом поля  над полем
над полем  .
.
Теорема 1. Конечное расширение  поля
поля  является алгебраическим расширением.
является алгебраическим расширением.
Пример 10. 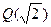 – конечное расширение поля
– конечное расширение поля  . Действительно, легко видеть, что система
. Действительно, легко видеть, что система 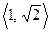 в данном случае является базисной. Отсюда
в данном случае является базисной. Отсюда 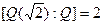 .
.
Теорема 2. Каждый элемент простого алгебраического расширения 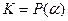 можно представить в виде многочлена от
можно представить в виде многочлена от 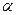 над полем
над полем  .
.
Следствие 1. Если 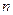 есть степень элемента
есть степень элемента 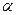 над полем
над полем  , то каждый элемент
, то каждый элемент 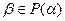
представляется многочленом над полем  , степень которого не превосходит
, степень которого не превосходит 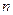 -1.
-1.
Следствие 2. Если 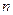 есть степень элемента
есть степень элемента 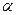 над полем
над полем  , то система элементов
, то система элементов 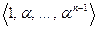 образует базис поля
образует базис поля  над полем
над полем  (т.н. степенной базис). Таким образом, поле
(т.н. степенной базис). Таким образом, поле 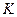 является конечным расширением поля
является конечным расширением поля  и
и 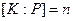 , т.е. степени присоединяемого элемента
, т.е. степени присоединяемого элемента 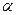 .
.
Пример 11. 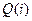 – поле гауссовых чисел является простым алгебраическим расширением поля
– поле гауссовых чисел является простым алгебраическим расширением поля  с базисом
с базисом 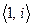 . Минимальный многочлен элемента i есть
. Минимальный многочлен элемента i есть 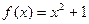 ,
, 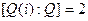 .
.
Теорема 3 (о степенях конечных расширений). Если в башне полей 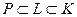 какие-либо две пары образуют конечные расширения, то и третья пара образует конечное расширение. При этом имеет место равенство
какие-либо две пары образуют конечные расширения, то и третья пара образует конечное расширение. При этом имеет место равенство 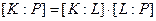 .
.
|
|
|
Пример 12. Пусть задана башня полей 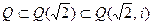 . В соответствии с теоремой, так как
. В соответствии с теоремой, так как 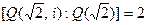 и
и 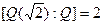 , получаем, что
, получаем, что 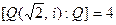 .
.
Пример 13. Пусть 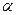 – корень многочлена
– корень многочлена 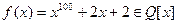 из примера 6. Его степень над полем
из примера 6. Его степень над полем  равна 100. Поэтому
равна 100. Поэтому 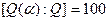 . Что можно сказать о степени
. Что можно сказать о степени 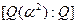 ?
?
Аналогом «Основной теоремы алгебры» служит следующая
Теорема 4 (Кронекера). Пусть  – поле и
– поле и 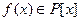 ,
, 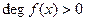 . Тогда существует конечное расширение поля
. Тогда существует конечное расширение поля  , в котором многочлен
, в котором многочлен 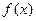 имеет корень.
имеет корень.
Следствие. В условиях теоремы существует конечное расширение поля  , над которым многочлен
, над которым многочлен 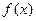 разлагается на линейные множители.
разлагается на линейные множители.
Это следствие вытекает легко из теоремы 3. Наконец, можно доказать и такой результат.
Теорема 5 (о примитивном элементе). Каждое конечное расширение является простым
алгебраическим.
Это, в частности, означает, что 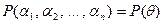 , для некоторого алгебраического элемента
, для некоторого алгебраического элемента 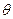 над
над  . Этот элемент и называют примитивным. Дадим еще
. Этот элемент и называют примитивным. Дадим еще
Определение 25. Пусть 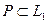 и
и 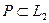 – поля. Если существует биективное отображение
– поля. Если существует биективное отображение 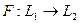 такое, что выполнены условия:
такое, что выполнены условия:
1) 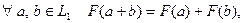
2) 
то говорят, поле 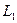 изоморфно полю
изоморфно полю 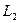 и пишут
и пишут 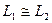 . Если при этом выполнено
. Если при этом выполнено
3) 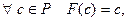
то изоморфизм называют относительным (относительно  ), а сами поля
), а сами поля 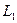 и
и 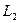 –
–
 -изоморфными.
-изоморфными.
Лемма 3. Бинарное отношение изоморфизма полей является отношением эквивалентности.
Свойства изоморфизма полей.
1) 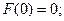
2) 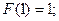
3) 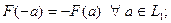
4) 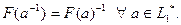
Пример 14. Можно показать, что 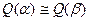 , где
, где 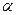 и
и 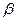 есть корни многочлена из примера 6.
есть корни многочлена из примера 6.
Определение 26. Пусть  – поле и
– поле и 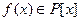 ,
, 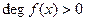 . Если
. Если 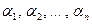 – все корни
– все корни 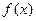 , то расширение
, то расширение 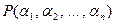 называется полем разложения многочлена
называется полем разложения многочлена 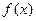 над полем
над полем  .
.
Пример 15. Полем разложения многочлена 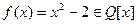 над полем
над полем  , очевидно, является поле
, очевидно, является поле 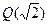 .
.
Пример 16. Полем разложения многочлена 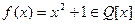 над полем
над полем  , очевидно, является поле
, очевидно, является поле 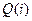 гауссовых чисел.
гауссовых чисел.
Теорема 6. Пусть  – поле,
– поле, 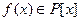 ,
, 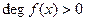 , тогда существует поле разложения многочлена
, тогда существует поле разложения многочлена 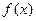 над полем
над полем  . Два любых поля разложения многочлена
. Два любых поля разложения многочлена 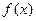 над
над  являются
являются  -изоморфными, а изоморфизм осуществляет некоторую перестановку корней этого многочлена.
-изоморфными, а изоморфизм осуществляет некоторую перестановку корней этого многочлена.
|
|
|
Определение 27. Пусть задано множество чисел 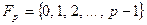 , где
, где 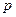 – простое число. Биекция
– простое число. Биекция 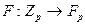 индуцирует на указанном множестве структуру конечного
индуцирует на указанном множестве структуру конечного
поля классов вычетов по простому модулю 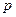 . И, таким образом,
. И, таким образом, 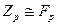 .Это поле
.Это поле
назовем полем Галуа порядка 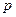 .
.
Как уже говорилось, каждое поле содержит простое подполе. Для таких подполей справедлива следующая
Теорема 7. Пусть  – поле и
– поле и 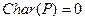 , тогда его простое подполе изоморфно полю
, тогда его простое подполе изоморфно полю  , а если
, а если 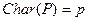 ,
, 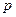 – некоторое простое число, то его простое подполе изоморфно полю
– некоторое простое число, то его простое подполе изоморфно полю 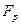 .
.
Задача 1. Доказать, что факторкольцо 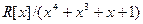 не может быть полем, каким бы ни было коммутативное кольцо
не может быть полем, каким бы ни было коммутативное кольцо  с единицей.
с единицей.
Задача 2. Показать, что для простого числа 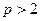 существует ровно два элемента
существует ровно два элемента 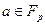 таких, что
таких, что  .
.
Задача 3. Доказать, что если 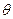 – алгебраический над полем
– алгебраический над полем  элемент, где
элемент, где  – алгебраическое расширение поля
– алгебраическое расширение поля  , то элемент
, то элемент 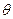 является алгебраическим и над полем
является алгебраическим и над полем  . Это значит, что если
. Это значит, что если 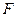 – алгебраическое расширение поля
– алгебраическое расширение поля  , то
, то 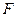 в то же время и алгебраическое расширение поля
в то же время и алгебраическое расширение поля  .
.
Задача 4. Доказать, что если  – расширение поля
– расширение поля  и степень
и степень  – простое число, то единственными полями
– простое число, то единственными полями 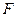 , удовлетворяющими условию
, удовлетворяющими условию 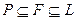 , являются
, являются 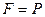 и
и 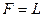 .
.
Задача 5. Расширения каких степеней над полем  можно получить, присоединяя к полю
можно получить, присоединяя к полю  корни многочлена
корни многочлена 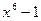 ? Описать получаемые расширения.
? Описать получаемые расширения.
Задача 6. Совпадают ли расширения 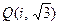 и
и 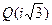 ?
?
Задача 7. Изоморфны ли поля 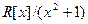 и
и 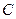 ? Можно ли сказать, что поля
? Можно ли сказать, что поля  -изоморфны?
-изоморфны?
Задача 8. Доказать, что матрицы вида 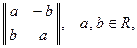 образуют поле изоморфное полю
образуют поле изоморфное полю 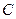 .
.
Задача 9. Построить поле разложения многочлена 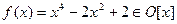 над полем
над полем  .
.
Задача 10. Построить поле разложения многочлена 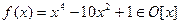 над полем
над полем  .
.
Раздел двадцатый
Конечные поля. Подполя конечного поля 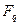 . Мультипликативная группа
. Мультипликативная группа 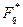 .
.
Первым конечным полем, как следует из предыдущих разделов, было поле классов вычетов по простому модулю 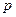 , т.е.
, т.е.  . Далее, был предложен его изоморфный образ
. Далее, был предложен его изоморфный образ 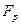 . Рассмотрим общий подход к описанию и построению конечных полей.
. Рассмотрим общий подход к описанию и построению конечных полей.
Лемма 1. Если 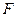 – конечное поле, являющееся расширением поля
– конечное поле, являющееся расширением поля  из q элементов, а
из q элементов, а 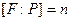 , то поле
, то поле 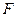 состоит из
состоит из 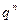 элементов.
элементов.
Лемма 2. Конечное поле 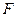 такое, что
такое, что 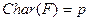 , состоит из
, состоит из 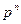 элементов, где
элементов, где 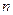 есть степень
есть степень 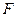 над его простым подполем.
над его простым подполем.
|
|
|
Последняя лемма есть прямое следствие предыдущей. Очевидно, что любое конечное поле имеет положительную характеристику. Теперь ясно, что количество элементов любого конечного поля есть некоторая натуральная степень его характеристики.
Лемма 3. Если 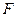 – конечное поле из
– конечное поле из 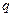 элементов, то для любого
элементов, то для любого 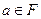 выполняется равенство
выполняется равенство 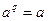 .
.
Из этой леммы, в частности, следует, что ненулевые элементы поля 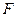 суть корни степени
суть корни степени 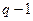 из мультипликативной единицы поля 1.
из мультипликативной единицы поля 1.
Лемма 4. Если 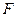 – конечное поле из
– конечное поле из 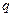 элементов, являющееся расширением поля
элементов, являющееся расширением поля  , и многочлен
, и многочлен 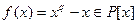 , то
, то 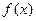 вполне разлагается над полем
вполне разлагается над полем 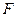 следующим образом:
следующим образом:
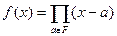 ,
,
так что поле 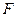 есть поле разложения многочлена
есть поле разложения многочлена 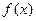 над полем
над полем  .
.
Наконец, опираясь на предыдущие леммы, можно доказать главный результат в виде следующей теоремы.
Теорема 1. (существование и единственность конечного поля). Для каждого простого числа 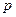 и каждого натурального числа
и каждого натурального числа 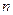 существует конечное поле из
существует конечное поле из 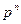 элементов. Любое конечное поле из
элементов. Любое конечное поле из 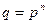 элементов изоморфно полю разложения многочлена
элементов изоморфно полю разложения многочлена 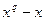 над полем
над полем 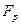 .
.
Эта теорема (своим выводом о единственности) позволяет говорить о вполне определенном поле данного порядка 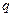 (т.е. о поле Галуа из
(т.е. о поле Галуа из 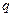 элементов). Это поле обозначают
элементов). Это поле обозначают 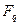 , где число
, где число 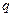 есть некоторая натуральная степень характеристики этого поля.
есть некоторая натуральная степень характеристики этого поля.
Теорема 2. (критерий подполя). Пусть 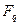 – конечное поле из
– конечное поле из 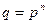 элементов, где
элементов, где 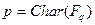 . Тогда каждое подполе поля
. Тогда каждое подполе поля 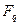 имеет порядок
имеет порядок 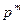 , где
, где 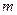 является делителем числа
является делителем числа 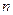 .
.
Обратно, если 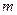 – положительный делитель числа
– положительный делитель числа 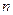 , то существует ровно одно подполе поля
, то существует ровно одно подполе поля 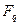 из
из 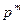 элементов.
элементов.
Если элементы поля 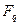 являлись корнями многочлена
являлись корнями многочлена 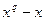 , то согласно последней теореме в нем содержится единственное подполе из
, то согласно последней теореме в нем содержится единственное подполе из 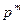 элементов для каждого положительного делителя
элементов для каждого положительного делителя 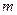 числа
числа 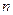 , и элементы этого подполя суть корни многочлена
, и элементы этого подполя суть корни многочлена 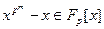 в поле
в поле 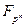 .
.
Пример 1. Подполя конечного поля 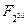 можно найти, составив список положительных делителей числа 30. Отношения включения между этими подполями указаны в следующей диаграмме.
можно найти, составив список положительных делителей числа 30. Отношения включения между этими подполями указаны в следующей диаграмме.
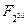
/ | \
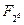

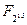
|
|
|
| / \ / \ |
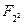
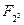
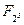
\ | /
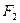
Следующий важный результат касается структуры мультипликативной группы конечного поля.
Теорема 3. Пусть 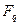 – конечное поле. Тогда мультипликативная группа этого поля
– конечное поле. Тогда мультипликативная группа этого поля 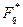 является циклической.
является циклической.
Определение 28. Образующий элемент циклической группы 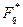 называется примитивным элементом поля
называется примитивным элементом поля 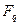 .
.
Здесь следует отметить отличие по смысловому содержанию этого понятия от того, что предлагалось в комментарии к теореме 5 из восемнадцатого раздела. Как известно, группа 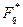 содержит
содержит 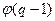 образующих элементов, где
образующих элементов, где  – функция Эйлера. Наличие примитивных элементов позволяет легко увидеть, что любое конечное поле есть простое алгебраическое расширение своего простого подполя.
– функция Эйлера. Наличие примитивных элементов позволяет легко увидеть, что любое конечное поле есть простое алгебраическое расширение своего простого подполя.
Теорема 4. Пусть 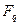 – конечное поле и
– конечное поле и 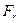 – его конечное расширение. Тогда
– его конечное расширение. Тогда 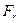 является простым алгебраическим расширением поля
является простым алгебраическим расширением поля 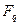 , причем образующим элементом этого простого расширения может служить любой примитивный элемент поля
, причем образующим элементом этого простого расширения может служить любой примитивный элемент поля 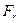 .
.
|
|
|
|
|
Дата добавления: 2014-11-16; Просмотров: 869; Нарушение авторских прав?; Мы поможем в написании вашей работы!