
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ускорением точки называется векторная величина , характеризующая быстроту изменения вектора скорости.
Определение ускорения точки
Пусть в некоторый момент времени t движущаяся точка находится в положении М и имеет скорость V, а в момент времени t1 приходит в положение М1 и имеет скоростьV1 (рисунок 1.3). Тогда за промежуток времени Dt=t1–t скорость точки получает приращение 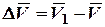
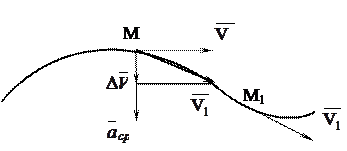 |

Рисунок 1.3
Для построения вектора 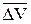 отложим от точки М вектор
отложим от точки М вектор 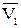 , и построим параллелограмм, в котором диагональю будет
, и построим параллелограмм, в котором диагональю будет 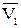 , а одной из сторон
, а одной из сторон  , тогда вторая сторона будет изображать вектор
, тогда вторая сторона будет изображать вектор 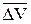 . Следует отметить, что вектор
. Следует отметить, что вектор 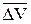 всегда направлен в сторону вогнутости траектории.
всегда направлен в сторону вогнутости траектории.
Отношение приращения вектора скорости 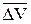 к соответствующему промежутку времени Dt определяет вектор среднего ускорения точки, за этот промежуток времени.
к соответствующему промежутку времени Dt определяет вектор среднего ускорения точки, за этот промежуток времени.
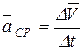 (1.5)
(1.5)
Вектор среднего ускорения имеет тоже направление, что и вектор 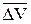 , т.е. направлен в сторону вогнутости траектории.
, т.е. направлен в сторону вогнутости траектории.
Ускорением точки в данный момент времени или мгновенным ускорением называется векторная величина 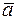 , к которой стремится среднее ускорение
, к которой стремится среднее ускорение 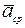 при стремлении промежутка времени Dt к нулю.
при стремлении промежутка времени Dt к нулю.
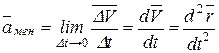 (1.6)
(1.6)
Следовательно, вектор мгновенного ускорения точки равен первой производной от вектора мгновенной скорости или второй производной от радиуса-вектора точки по времени.
Размерность ускорения [м/с2].
При прямолинейном движении точки вектор ускорения точки 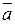 направлен вдоль прямой, по которой движется точка. Если траекторией точки является плоская кривая, то вектор ускорения
направлен вдоль прямой, по которой движется точка. Если траекторией точки является плоская кривая, то вектор ускорения 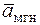 , также как и вектор
, также как и вектор 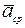 лежит в плоскости этой кривой и направлен в сторону её вогнутости.
лежит в плоскости этой кривой и направлен в сторону её вогнутости.
1.2 Координатный способ задания движения точки
Положение точки можно непосредственно определять её декартовыми координатами X,Y,Z, которые при движении точки будут с течением времени изменяться. Чтобы знать закон движения точки, т.е. её положение в пространстве в любой момент времени, надо знать значение координат точки в каждый момент времени, т.е. знать зависимости:
X=f1(t); Y=f2(t); Z=f3(t) (1.7)
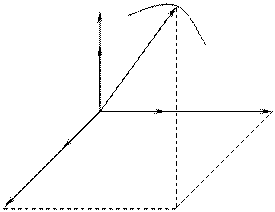
которые представляют собой уравнения движения точки в прямоугольных декартовых координатах (рисунок 1.4).
 M
M
z
z
y
о 
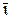
x
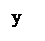 x
x
Рисунок 1.4
Эти уравнения представляют собой закон движения точки при координатном способе задания движения.
Если движение точки происходит на плоскости XOY, то в этом случае будет два уравнения движения:
X = f1 (t) и Y = f2 (t) (1.8)
При прямолинейном движении точки, например, вдоль оси X, будет одно уравнение движения:
X = f (t) (1.9)
Уравнения (1.7) и (1.8) представляют собой одновременно уравнение траектории точки в параметрической форме, где роль параметра играет время t. Чтобы получить уравнение траектории точки уравнения (1.7) или (1.8) решают совместно, исключая время t, поэтому уравнения траектории представляет собой зависимость между координатами точки:
X = f1 (y) или Y = f2 (x) (1.10)
Определение скорости и ускорения точки
Из рисунка 1.4 следует, что:
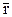 =
= 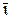 x +
x + 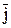 y +
y + 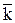 z
z
тогда, используя выражение (1.4), получим, что вектор скорости точки
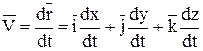 или
или
т.к.  =
= 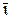 Vx +
Vx + 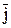 Vy +
Vy + 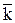 Vz, получим, что
Vz, получим, что
Vx = 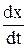 ; Vy =
; Vy = 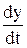 ; Vz =
; Vz = 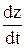 , (1.11)
, (1.11)
где Vx, Vy, Vz – проекции вектора скорости V на оси координат, а x, y, z – проекции вектора 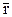 на эти же оси координат, т.е. проекции скорости точки на координатные оси равны первым производным от соответствующих координат точки по времени.
на эти же оси координат, т.е. проекции скорости точки на координатные оси равны первым производным от соответствующих координат точки по времени.
Зная проекции скорости, найдём её модуль и направление (т.е. углы a, b, g, которые вектор  образует с осями координат), по формулам:
образует с осями координат), по формулам:
V= 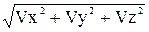
 (1.12)
(1.12)

 cosa =
cosa = 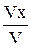 ; cosb =
; cosb = 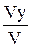 ; cosg =
; cosg = 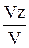 . (1.13)
. (1.13)
Вектор ускорения точки 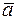 =
= 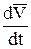 , поэтому
, поэтому 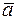 =
= 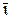
 , но т.к.
, но т.к. 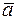 =
= 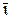 a x +
a x + 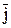 a y +
a y + 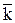 a z, то
a z, то
a x = 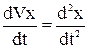 ; a y =
; a y = 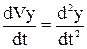 ; a z =
; a z = 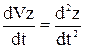 ; (1.14)
; (1.14)
Т.е. проекции ускорения точки на координатные оси равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени.
Модуль и направление ускорения найдутся по формулам:
a = 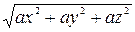 (1.15)
(1.15)
cosa1 = 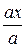 ; cosb1 =
; cosb1 = 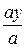 ; cosg1 =
; cosg1 = 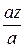 (1.16)
(1.16)
где a1, b1, g1 – углы, образуемые вектором ускорения с осями координат.
Если движение точки происходит на плоскости, то в формулах (1.11), (1.12), (1.14), (1.15) должна быть отброшена одна из проекций; при прямолинейном движении будет:
Vх = 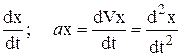 (1.17)
(1.17)
1.3 Естественный способ задания точки
Данным способом задания движения удобно пользоваться в том случае, когда траектория движущейся точки известна заранее. В этом случае на траектории выбирают какую-нибудь неподвижную точку О за начало отсчёта и устанавливают на траектории положительное и отрицательное направление отсчёта. Тогда положение точки М на криволинейной траектории (рисунок 1.5) будет однозначно определяться криволинейной координатой S которая равна расстоянию от точки О до точки М, измеренному вдоль дуги траектории и взятому с соответствующим знаком.
 A -O+
A -O+
 | |||
 | |||

 z M
z M
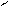 M1
M1


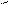 M2
M2
o y B
x
Рисунок 1.5
При движении точка М перемещается в положение М1, М2.., следовательно, расстояние S будет с течением времени меняться. Чтобы знать положение точки М на траектории в любой момент времени надо знать зависимость
S = f (t) (1.18)
Уравнение (1.18) выражает закон движения точки М вдоль траектории. Таким образом, чтобы задать движение точки естественным способом, надо задать:
1. Траекторию точки; 2. Начало отсчёта на траектории; 3. Положительное и отрицательное направления движения; 4. Закон движения точки вдоль траектории: S = f (t).
Вычисление скорости и ускорения точки
В этом случае значение векторов  и
и 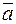 определяют по их проекциям не на оси системы отсчёта ОХУZ, как в предыдущих случаях, а на подвижные оси М τ n b, имеющие начало в точке М и движущиеся вместе с ней. Эти оси, называемые осями естественного трёхгранника, направлены следующим образом: ось Мτ – по касательной к траектории в сторону положительного направления отсчёта расстояния S; ось Мn – по нормали к траектории, лежащей в соприкасающейся плоскости и направленной в сторону вогнутости траектории; ось Мb – перпендикулярно к первым двум так, чтобы она образовывала с ними правую систему осей. Нормаль Мn – называется главной нормалью, а ось Мb – бинормалью (рисунок 1.6).
определяют по их проекциям не на оси системы отсчёта ОХУZ, как в предыдущих случаях, а на подвижные оси М τ n b, имеющие начало в точке М и движущиеся вместе с ней. Эти оси, называемые осями естественного трёхгранника, направлены следующим образом: ось Мτ – по касательной к траектории в сторону положительного направления отсчёта расстояния S; ось Мn – по нормали к траектории, лежащей в соприкасающейся плоскости и направленной в сторону вогнутости траектории; ось Мb – перпендикулярно к первым двум так, чтобы она образовывала с ними правую систему осей. Нормаль Мn – называется главной нормалью, а ось Мb – бинормалью (рисунок 1.6).
 |

 z
z
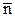
 – О +
– О + 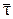

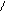





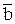
х
Рисунок 1.6
Скорость точки, направленная по касательной к траектории (рисунок 1.6) определяется только одной проекцией Vτ на ось Mτ, при этом Vτ = V или Vτ = -V: т.е. Vτ или совпадает с модулем скорости V, или отличается от V только знаком. Поэтому в дальнейшем будем обозначать скорость точки V и называть V – числовым (или алгебраическим) значением скорости.
Найдём значение V: если обозначить DS – приращение координаты S при перемещении точки из положения М в М1, то численно средней скоростью точки за этот промежуток времени будет
Vср= 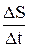 или в пределе V =
или в пределе V = 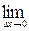
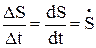 (1.19)
(1.19)
Вектор 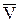 =
= 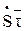 (1.20)
(1.20)
Таким образом, числовое значение скорости точки в данный момент времени равно первой производной от расстояния (криволинейной координаты) S этой точки по времени.
Величина V одновременно определяет и модуль скорости, и сторону, куда она направлена.
Ранее было установлено, что ускорение 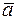 точки направленно в сторону вогнутости траектории, т.е. в соприкасающейся плоскости Mτ. Следовательно, проекция
точки направленно в сторону вогнутости траектории, т.е. в соприкасающейся плоскости Mτ. Следовательно, проекция 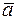 на бинормаль Mb равна нулю (ab=0). Найдём проекции
на бинормаль Mb равна нулю (ab=0). Найдём проекции 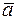 на две другие оси, проектируя (1.6) на оси Mτ и Mn:
на две другие оси, проектируя (1.6) на оси Mτ и Mn:
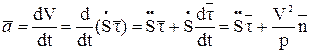 (1.21)
(1.21)
т.к. 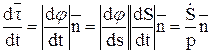 ;
;
где 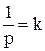 – кривизна траектории;
– кривизна траектории;
р – радиус кривизны траектории, который считаем положительным.
Получим разложение ускорения точки по осям естественного трёхгранника: 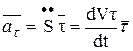 (1.21) – называется касательным ускорением;
(1.21) – называется касательным ускорением; 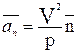 (1.22) – называется нормальным ускорением.
(1.22) – называется нормальным ускорением.
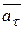 – всегда направлен по касательной к траектории в данной точке по оси τ;
– всегда направлен по касательной к траектории в данной точке по оси τ; 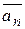 – направлен в сторону вогнутости траектории, по оси
– направлен в сторону вогнутости траектории, по оси 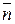 ;
; 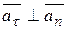 ; (рисунок 1.7).
; (рисунок 1.7).

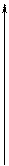 z
z 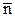


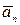
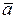

b
М 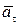
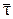

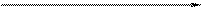
o y
x
Рисунок 1.7
Таким образом, ускорение точки
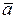 =
= 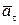 +
+ 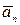 (1.23)
(1.23)
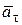 – измеряет быстроту изменения скорости по величине;
– измеряет быстроту изменения скорости по величине;
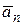 – измеряет быстроту изменения скорости по направлению.
– измеряет быстроту изменения скорости по направлению.
 M1
M1 

N2 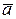 =
= 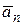
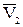
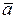 =
= 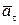 +
+ 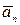 V = const
V = const
Переменное криволинейное движение Равномерное движение по окружности
М 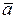
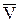



a= aτ
|
|
Дата добавления: 2014-11-08; Просмотров: 1656; Нарушение авторских прав?; Мы поможем в написании вашей работы!