
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Определение производной, дифференциала
Тема 5. Производная и дифференциал функции одного аргумента.
Пискунов, гл. III, § 1-26, упр 1-220
Гл. IV, § 1-7, упр 1-55.
1. Определение. Производной первого порядка от функции 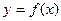 по аргументу xназывается предел отношения приращения функции
по аргументу xназывается предел отношения приращения функции 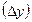 к приращению аргумента
к приращению аргумента 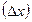 при условии, что
при условии, что 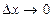 , т.е.
, т.е. 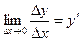 или
или 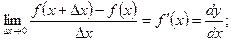
2. 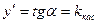 , где a- угол наклона касательной к
, где a- угол наклона касательной к 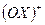
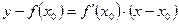 - уравнение касательной, проведённой в т.
- уравнение касательной, проведённой в т. 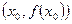
3. 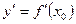 - скорость изменения функции в т. x0.
- скорость изменения функции в т. x0.
- Отыскание производной называется дифференцированием.
-
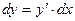 - дифференциал функции равен произведению производной функции на дифференциал аргумента.
- дифференциал функции равен произведению производной функции на дифференциал аргумента.
Геометрически dy представляет собой приращение ординаты касательной к графику функции в заданной точке.
6. 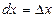 - дифференциал аргумента равен приращению аргумента.
- дифференциал аргумента равен приращению аргумента.
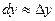 - дифференциал функции и приращение функции равны лишь приближённо.
- дифференциал функции и приращение функции равны лишь приближённо.
7. 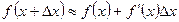 - формуладляприближённыхвычислений.
- формуладляприближённыхвычислений.
Таблица дифференциалов и производных основных элементарных функций.
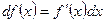
| Элементарные функции | дифференциал | производная |
1. Степенная функция 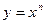
| 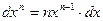
| 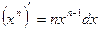
|
2. Линейная функция 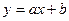 a,b-постоянные
y=x. a,b-постоянные
y=x.
| 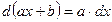
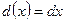
| 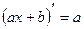
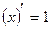
|
| 3.Тригонометрич. функции y=sin x y=cos x y=tg x y=ctg x |
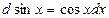
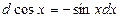
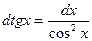
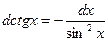
|
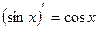
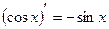
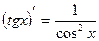
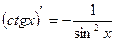
|
4. Показательная функция
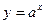 , a -число , a -число
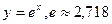
|
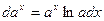
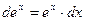
| 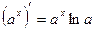
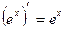
|
5. Логарифмическая функция
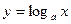 y=ln x
y=ln x
| 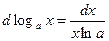
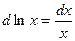
| 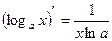
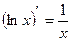
|
6. Иррациональная функция
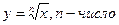
| 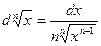
| 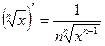
|
| 7. Обратно тригонометричес- кие функции y= arcsin x y=arcos x y= arctg x y=arcctg x |
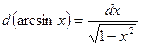
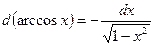
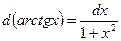
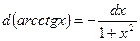
|
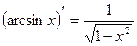
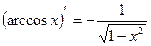
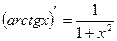
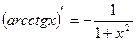
|
| 8. y=c c-const | d(c)=0·dx | 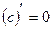
|
Основные правила дифференцирования.
Пусть С- постоянное, 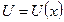 и
и 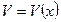 - функции имеющие производные.
- функции имеющие производные.
Тогда:
1) 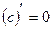
2) 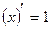
3) 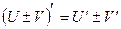
4) 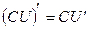
5) 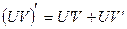
6) 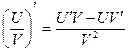
7) если 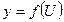 ,
, 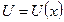 , т.е
, т.е 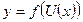 , где функции f(U) и U(x) имеют производные, то
, где функции f(U) и U(x) имеют производные, то 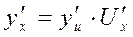 - правило дифференцирования сложной функции.
- правило дифференцирования сложной функции.
5.2 Примеры решения задач.
Задача 1. Найти производные 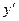 или
или 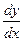 следующих функций:
следующих функций:
а) 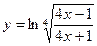
б) 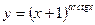
в) 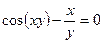
г) 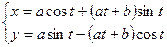
Решение:
а) Пользуясь правилом логарифмирования корня и дроби, преобразуем правую часть:
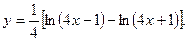
Применяя правила и формулы дифференцирования, получим:
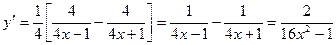
б) Предварительно прологарифмируем по основанию е обе части равенства:
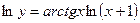
Теперь дифференцируем обе части, считая 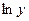 сложной функцией от переменной х:
сложной функцией от переменной х:

откуда
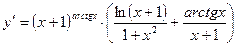
в) В данном случае зависимость между аргументом х и функцией у задана уравнением, которое не разрешено относительно функции у. Чтобы найти производную у', следует дифференцировать по х обе части заданного уравнения, считая при этом у функцией от х, а затем полученное уравнение решить относительно искомой производной у'. Имеем
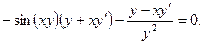
Из полученного равенства, связывающего х, у, и у',
находим производную у':
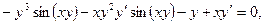
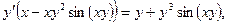
откуда
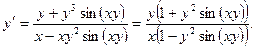
г) Зависимость между переменными х и у задана параметрическими уравнениями. Чтобы найти искомую производную у', находим предварительно дифференциалы dy и dx и затем берем отношение этих дифференциалов
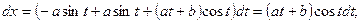
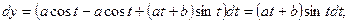
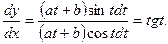
Задача 2. Найти производную второго порядка 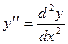
а) 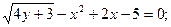
б) 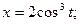
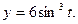
Решение: а) Функция у задана в неявном виде. Дифференцируем по х обе части заданного уравнения, считая при этом у функцией от х:
|
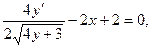
откуда 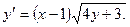
Снова дифференцируем по х обе части (1):
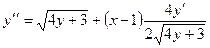 (2)
(2)
Заменив у' в (2) правой частью (1), получим:
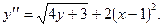
б) Зависимость между переменными xи у задана параметрическими уравнениями. Чтобы найти производную у', находим сперва дифференциалы dy и dx и затем берем отношение этих дифференциалов:
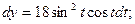
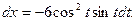
Тогда
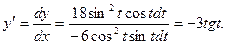
Производная второго порядка 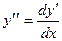 . Следовательно, чтобы найти у", надо найти дифференциал dy':
. Следовательно, чтобы найти у", надо найти дифференциал dy': 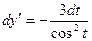
Тогда 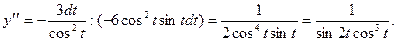
Задача 3. Найти приближенное значение функции 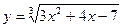 при
при 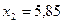 исходя из ее точного значения при
исходя из ее точного значения при 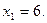
Решение: Известно, что дифференциал dy функции 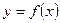 представляет собой главную часть приращения этой функции
представляет собой главную часть приращения этой функции 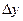 .Если приращение аргумента
.Если приращение аргумента 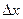 мало по абсолютной величине, то приращение
мало по абсолютной величине, то приращение 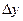 приближенно равно дифференциалу, т. е.
приближенно равно дифференциалу, т. е. 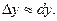 . Так как
. Так как 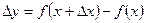 , а
, а 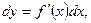 то имеет место приближенное равенство:
то имеет место приближенное равенство:
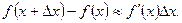
Пусть 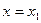 ,
, 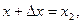 т. е.
т. е. 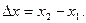
Тогда 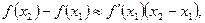
|
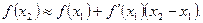
Приближенное равенство (1) дает возможность найти значение функции при  , если известно значение функции и ее производной при
, если известно значение функции и ее производной при 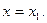 Прежде чем воспользоваться приближенным равенством (1), находим числовое значение производной f'(x) при х= 6:
Прежде чем воспользоваться приближенным равенством (1), находим числовое значение производной f'(x) при х= 6:
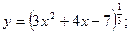
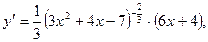 или
или 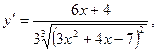
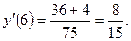
Применяя (1), получаем
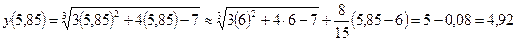
|
|
Дата добавления: 2014-11-16; Просмотров: 536; Нарушение авторских прав?; Мы поможем в написании вашей работы!