
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример. Дифференциальные уравнения
|
|
|
|
Дифференциальные уравнения.
Пример.
Пример.
а) 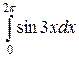 . Применяя формулу Ньютона-Лейбница, вычислим этот интеграл:
. Применяя формулу Ньютона-Лейбница, вычислим этот интеграл:
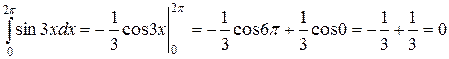
б) 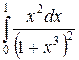 . Вычислим этот интеграл, используя метод замены переменной:
. Вычислим этот интеграл, используя метод замены переменной:
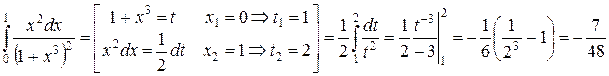
в) 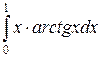 . Применяя формулу интегрирования по частям получим:
. Применяя формулу интегрирования по частям получим:
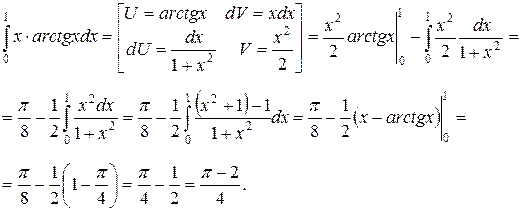
121.-130. Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж.
121. 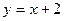 ,
, 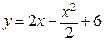 . 126.
. 126. 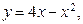
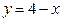
122. 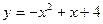 ,
, 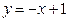 . 127.
. 127. 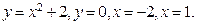
123. 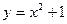 ,
, 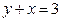 . 128.
. 128. 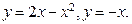
124. 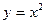 ,
, 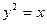 . 129.
. 129. 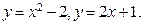
125. 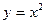 ,
, 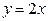 . 130.
. 130. 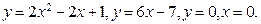
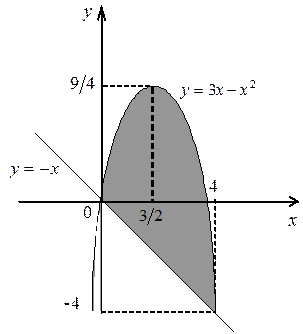
а) Вычислить площадь фигуры, ограниченной параболой 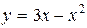 и прямой
и прямой  .
.
Находим точки пересечения данных кривых и строим искомую фигуру
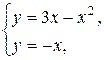
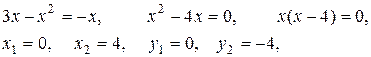
Площадь фигуры, ограниченной снизу кривой 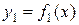 , сверху – кривой
, сверху – кривой 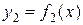 , вычисляет интеграл
, вычисляет интеграл 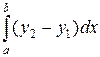 , где
, где 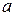 и
и 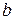 - абсциссы точек пересечения этих кривых, причем
- абсциссы точек пересечения этих кривых, причем 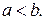
Следовательно, имеем
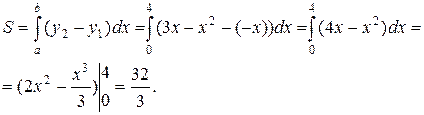
131 – 140. Найти общее решение дифференциального уравнения.
131. а). 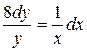 ; б).
; б). 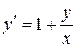 ; в).
; в). 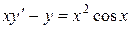 .
.
132. а). 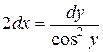 ; б).
; б). 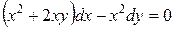 ; в).
; в). 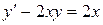 .
.
133. а). 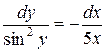 ; б).
; б). 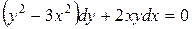 ; в).
; в). 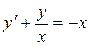 .
.
134. а). 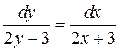 ; б).
; б). 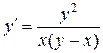 ; в).
; в). 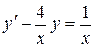 .
.
135. а). 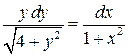 ;б).
;б). 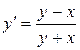 ; в).
; в). 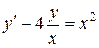 .
.
136. а). 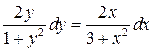 ; б).
; б). 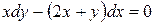 ; в).
; в). 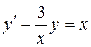 .
.
137. а). 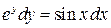 ; б).
; б). 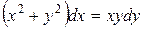 ; в).
; в). 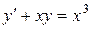 .
.
138. а). 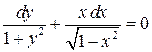 ; б).
; б). 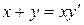 ; в).
; в). 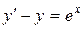 .
.
139. а). 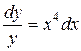 ; б).
; б). 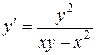 ; в).
; в). 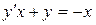 .
.
140. а).  ; б).
; б). 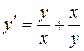 ; в).
; в). 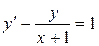 .
.
а) 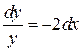 .
.
Данное уравнение является уравнением с разделенными переменными. Проинтегрируем обе его части:
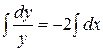 , получим:
, получим: 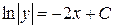 .
.
б). 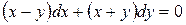 .
.
Для решения данного уравнения используем тот факт, что 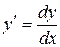 . Так как переменные в данном случае разделить нельзя, то выразим
. Так как переменные в данном случае разделить нельзя, то выразим 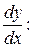
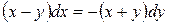 , отсюда по правилу пропорции получаем:
, отсюда по правилу пропорции получаем:
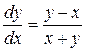 , или
, или 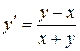 .
.
В данном случае 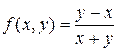 ;
; 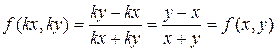 .
.
Следовательно, данное уравнение – однородное. Делаем замену переменной
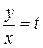 ,
, 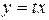 ,
, 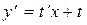 . После замены получим:
. После замены получим:
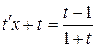 ,
, 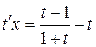 ,
, 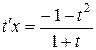 .
.
Получили уравнение с разделяющимися переменными. Разделяя переменные, получим: 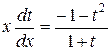 ,
, 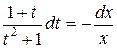 .
.
Интегрируя, находим общее решение
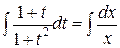 ,
, 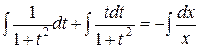 ,
,
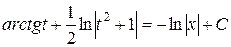 .
.
Возвращаясь к старой переменной, получаем общий интеграл
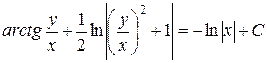 .
.
в). 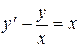 .
.
Данное уравнение линейное. Ищем решение в виде 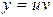 ,
, 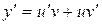 .
.
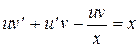 ,
, 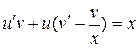 .
.
Решаем уравнение. 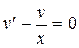 ,
, 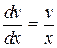 ,
, 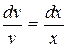 ,
, 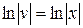 ,
, 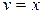 .
.
Подставляя полученное значение 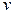 в уравнение, имеем:
в уравнение, имеем:
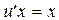 ,
, 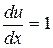 ,
, 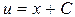 .
.
Общее решение 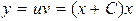 или
или 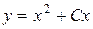 .
.
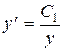 ,
, 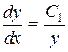 ,
, 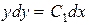 ,
, 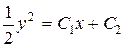 .
.
141–150. Найти общее решение дифференциального уравнения:
141. а). 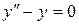 ; б).
; б). 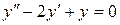 ; в).
; в). 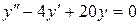 .
.
142. а). 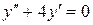 ; б).
; б). 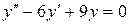 ; в).
; в). 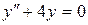 .
.
143. а). 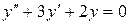 ; б).
; б). 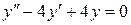 ; в).
; в). 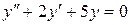 .
.
144. а). 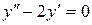 ; б).
; б). 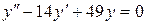 ; в).
; в). 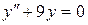 .
.
145. а). 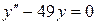 ; б).
; б). 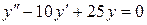 ; в).
; в). 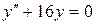 .
.
146. а). 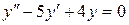 ; б).
; б). 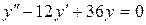 ; в).
; в). 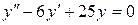 .
.
147. а). 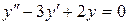 ; б).
; б). 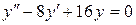 ; в).
; в). 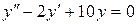 .
.
148. а). 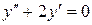 ; б).
; б). 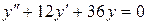 ; в).
; в). 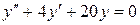 .
.
149. а). 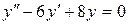 ; б).
; б). 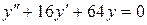 ; в).
; в). 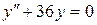 .
.
150. а). 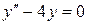 ; б).
; б). 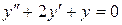 ; в).
; в). 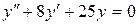 .
.
Пример. а). 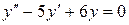 .
.
Составим соответствующее характеристическое уравнение:
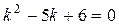 ,
,
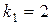 ,
, 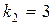 .
.
Так как корни характеристического уравнения 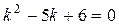 действительные, различные, следовательно, общее решение однородного уравнения имеет вид
действительные, различные, следовательно, общее решение однородного уравнения имеет вид 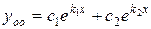 , то есть имеем
, то есть имеем
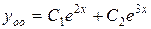 .
.
б). 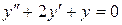 .
.
Составим соответствующее характеристическое уравнение:
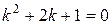 ,
,
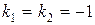 .
.
Так как корни характеристического уравнения 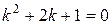 действительные, одинаковые, следовательно, общее решение однородного уравнения имеет вид
действительные, одинаковые, следовательно, общее решение однородного уравнения имеет вид 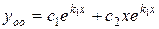 , то есть имеем
, то есть имеем
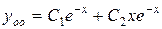 .
.
в). 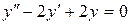 .
.
Составим соответствующее характеристическое уравнение:
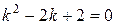 . Решим его при помощи вычисления дискриминанта:
. Решим его при помощи вычисления дискриминанта:
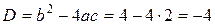 . Так как в данном случае
. Так как в данном случае 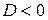 , то для вычисления квадратного корня
, то для вычисления квадратного корня 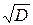 используем равенство
используем равенство 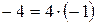 . Так как
. Так как 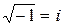 (комплексная единица), то в данном случае
(комплексная единица), то в данном случае 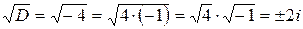 . Таким образом, имеем в данном случае комплексные корни:
. Таким образом, имеем в данном случае комплексные корни:
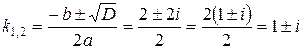 .
.
Так как корни характеристического уравнения 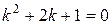 комплексно-сопряженные, следовательно, общее решение однородного уравнения имеет вид
комплексно-сопряженные, следовательно, общее решение однородного уравнения имеет вид 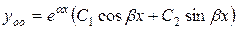 , где
, где 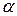 и
и 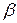 - соответственно действительная и мнимая части комплексных корней. В данном случае
- соответственно действительная и мнимая части комплексных корней. В данном случае 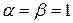 . Таким образом, общее решение исходного уравнения имеет вид:
. Таким образом, общее решение исходного уравнения имеет вид:
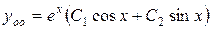 .
.
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 447; Нарушение авторских прав?; Мы поможем в написании вашей работы!