Метод Гауса-Зейделя

Метод Зейделя являє собою модифікацію метода послідовних наближень, при чому у методі Зейделя при обчисленні і -ої координати вектора розв’язку 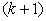- го наближення використовуються значення всіх (і-1) координат вектора 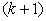- е наближення обчислені раніше. Розглянемо метод більш детально.

Нехай початкова система лінійних алгебраїчних рівнянь приведена до нормального вигляду:

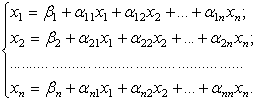(3.17)

Алгоритм Гауса-Зейделя

Вибрати значення координат вектора початкових наближень

Визначити значення першої координати 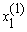вектора першого наближення з першого рівняння системи:

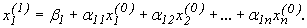
Підставити в друге рівняння системи значення першої координати 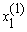, яке обчислено на попередньому кроці

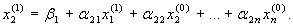
Отримані значення координат першого наближення 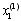, 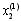підставляємо у третє рівняння системи (3.14)

для знаходження третій координати і т.д.

1. Для знаходження останньої координати вектора першого наближення 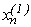в останнє рівняння системи треба підставити значення всіх (n-1) координат (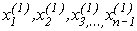), які отримані на попередніх кроках та значення координати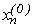

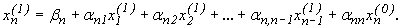
6. Аналогічно будують друге, третє та інші наближення. Так для вектора (k+1) -го наближення за методом Зейделя використовуют наступні формули:

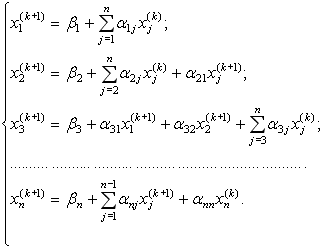(3.18)

Умови збіжності ітераційного процесу Зейделя

Даний процес розв’язання СЛАР - ітераційний, тому важливим є аналіз умов збіжності ітераційного процесу. Процес Зейделя для системи лінійних рівнянь 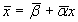збігається до точного розв’язку с заданою похибкою 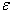при будь-якому виборі вектора початкових наближеннь, якщо будь яка норма матриці 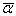менша 1, тобто якщо:

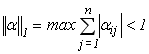(3.19)

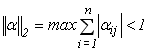(3.20)

(3.21)

Відомо, що процес Зейделя сходиться до точного розв’язку СЛАР швидше ніж метод послідовних наближень.

Приклад. Знайти першу та другу норми та проаналізувати умови збіжності ітераційного процесу для матриці 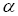, яка має вигляд:

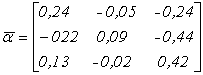
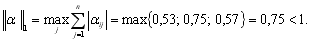
Очевидно, що процес ітерації для даної системи сходиться до точного розв’язку, не дивлячись на те, що

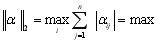{0,59; 0,16; 1,1}=1,1>1.

Оцінка похибки методу Гауса-Зейделя

Якщо 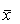- точне значення вектора розв’язку системи лінійних рівнянь; а - к-е наближення, обчислене за методом Гауса-Зейделя, то для оцінки похибки цього метода використовується формула:

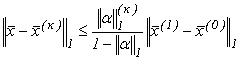(3.22)

Дата добавления: 2014-11-08