
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Математична постановка задачі інтерполювання
|
|
|
|
В економіці і техніці постійно приходиться зіштовхуватися з необхідністю обчислення значень функції 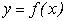 в точках
в точках 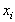 , відмінних від значень аргументу, фіксованих в таблиці експериментальних досліджень. Крім того, в деяких випадках, незважаючи на те, що аналітичний вираз функції
, відмінних від значень аргументу, фіксованих в таблиці експериментальних досліджень. Крім того, в деяких випадках, незважаючи на те, що аналітичний вираз функції 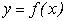 відомий, він є занадто складним і незручним для подальших математичних перетворень. Подібні задачі формалізуються як задачі інтерполювання.
відомий, він є занадто складним і незручним для подальших математичних перетворень. Подібні задачі формалізуються як задачі інтерполювання.
Нехай на відрізку  функція
функція 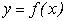 задана системою точок
задана системою точок 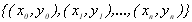 , де значення
, де значення 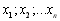 називаються вузлами інтерполяції. Необхідно знайти аналітичну залежність
називаються вузлами інтерполяції. Необхідно знайти аналітичну залежність  , співпадаючої у вузлах інтерполяції зі значеннями заданої функції, тобто
, співпадаючої у вузлах інтерполяції зі значеннями заданої функції, тобто 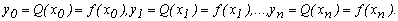 Процес обчислення значень функції
Процес обчислення значень функції  в точках
в точках 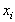 , відмінних від вузлів інтерполяції, називають інтерполюванням функції
, відмінних від вузлів інтерполяції, називають інтерполюванням функції 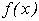 (рисунок 5.1).
(рисунок 5.1).
Якщо аргумент 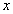 знаходиться за межами відрізка інтерполювання
знаходиться за межами відрізка інтерполювання  , то задача визначення значення функції
, то задача визначення значення функції  в точці
в точці 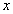 називається екстраполюванням.
називається екстраполюванням.
Слідує відмітити, що задача інтерполювання стає однозначною, якщо в якості функції  вибрати багаточлен
вибрати багаточлен 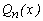 степені не вище n, такий, що
степені не вище n, такий, що 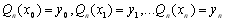 . Багаточлен
. Багаточлен 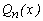 , що задовольняє цим умовам, називають інтерполяційним багаточленом, а відповідні формули – інтерполяційними формулами.
, що задовольняє цим умовам, називають інтерполяційним багаточленом, а відповідні формули – інтерполяційними формулами.
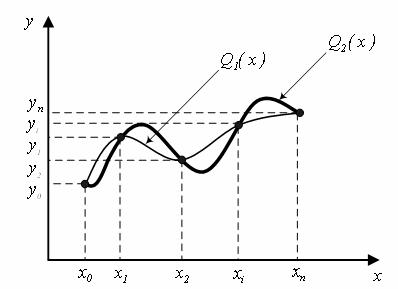
Рисунок 5.2 – Геометрична інтерпретація інтерполяції табличної функції
У випадку, коли  береться з класу степеневих функцій, інтерполяція називається параболічною. Цей спосіб наближення ґрунтується на тому, що на невеликих відрізках експериментальна функція
береться з класу степеневих функцій, інтерполяція називається параболічною. Цей спосіб наближення ґрунтується на тому, що на невеликих відрізках експериментальна функція 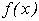 може бути достатньо добре апроксимована параболою певного порядку. Якщо в якості інтерполяційної функції використовувати багаточлен виду:
може бути достатньо добре апроксимована параболою певного порядку. Якщо в якості інтерполяційної функції використовувати багаточлен виду:
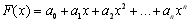 (5.1)
(5.1)
то така інтерполяція називається степеневою
Інколи доцільно використати інші види інтерполяції. Якщо функція, що досліджується, 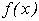 – періодична, то в якості інтерполяційної функції
– періодична, то в якості інтерполяційної функції 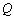 (
(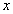 ) вибирають тригонометричну, наприклад, виду:
) вибирають тригонометричну, наприклад, виду:
|
|
|
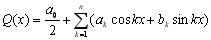 (5.2)
(5.2)
і така інтерполяція називається тригонометричною. В деяких в якості інтерполяційної функції 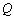 (
(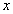 ) вибирають раціональні функції.
) вибирають раціональні функції.
При інтерполюванні виникає ряд задач:
1. вибір найбільш зручного способу побудови інтерполяційної функції для кожного конкретного випадку;
2. оцінка похибки при заміні 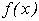 інтерполяційною функцією
інтерполяційною функцією  на відрізку
на відрізку  , оскільки функції
, оскільки функції 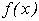 та
та  співпадають тільки у вузлах інтерполяції
співпадають тільки у вузлах інтерполяції 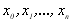 ;
;
3. оптимальний вибір вузлів інтерполяції для отримання мінімальної похибки.
Для задачі інтерполювання важливим є визначення того, як повинна вести себе інтерполяційна функція між заданими точками, так як ці точки можуть бути інтерпольовані множиною різноманітних функцій, і необхідно мати певний критерій вибору. Звичайно критерій формується в термінах гладкості та простоти. Більшість інтерполяційних функції генеруються лінійними комбінаціями найпростіших функцій. Лінійні комбінації одночленів 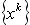 формують степеневі поліноми, лінійні комбінації тригонометричних функцій
формують степеневі поліноми, лінійні комбінації тригонометричних функцій 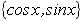 формують тригонометричні поліноми, використовуються також лінійні комбінації експонент
формують тригонометричні поліноми, використовуються також лінійні комбінації експонент 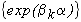 . Найбільш важливим класом інтерполяційних функцій є множина алгебраїчних поліномів. Поліноми мають переваги з точки зору алгоритмізації, тому що їх значення легко обчисляти, додавати, перемножувати, інтегрувати чи диференціювати. Важливою властивістю поліномів є те що якщо с – константа, а p(x)- поліном, то поліномами будуть і p(cx) і p(x+c)
. Найбільш важливим класом інтерполяційних функцій є множина алгебраїчних поліномів. Поліноми мають переваги з точки зору алгоритмізації, тому що їх значення легко обчисляти, додавати, перемножувати, інтегрувати чи диференціювати. Важливою властивістю поліномів є те що якщо с – константа, а p(x)- поліном, то поліномами будуть і p(cx) і p(x+c)
Клас інтерполяційних функції обирають, використовуючи теорему Вейерштраса:
Якщо f(х) – неперервна на кінцевому інтервалі 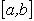 функція, то для любого
функція, то для любого 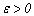 існують поліном pn(x) ступеня n такий, що
існують поліном pn(x) ступеня n такий, що 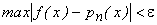 .
.
|
|
|
|
|
Дата добавления: 2014-11-08; Просмотров: 976; Нарушение авторских прав?; Мы поможем в написании вашей работы!