Рынки активов в условиях неопределенности

Активы – это средства, обеспечивающие поток доходов их владельцу в форме прямых выплат (например, прибыль, дивиденды, рента и пр.) и срытых выплат (увеличение стоимости недвижимости, курса акций и т.д.). Норма отдачи от актива (без учета инфляции) определяется как отношение всех денежных поступлений от актива к цене его приобретения.

Активы делятся на два вида по степени риска. Безрисковые активы – это активы, дающие поток доходов, размеры которого известны заранее. Рисковые активы – это активы, будущий доход от которых сейчас не определен.

В предыдущих параграфах исследовалась модель выбора в условиях неопределенности, построенная с использованием функции ожидаемой полезности. Альтернативный подход к задачам выбора в условиях неопределенности состоит в том, чтобы описать распределение будущего потока доходов по вероятностям с помощью нескольких параметров.

Один из примеров реализации такого подхода — модель средней и дисперсии относительно нее. В этом случае предполагается, что предпочтения экономических агентов могут быть описаны с помощью нескольких статистических выводов в отношении распределения вероятностей их богатства.

Допустим, что случайная переменная w, характеризующая богатство, принимает значения w_s, для s= 1,…,Sс вероятностью π_s. Средняя распределения вероятностей есть среднее взвешенное по вероятностям значение w:

(10.14)

Дисперсия распределения вероятностей богатства есть среднее значение величины . Это средневзвешенная величина квадратов отклонений действительных результатов от ожидаемых:

(10.15)

Дисперсия измеряет «разброс» распределения и является подходящей мерой степени имеющегося риска. Тесно связана с ней такая величина, как стандартное отклонение, обозначаемое σ_w, которое является квадратным корнем из дисперсии:

(10.16)

Средняя распределения вероятностей измеряет среднее значение богатства — то, вокруг которого сосредоточено распределение. Дисперсия распределения измеряет «разброс» распределения — то, каким образом оно рассеивается вокруг средней. На рис. 5 графически представлено распределений вероятностей с различными средними и дисперсиями.

Средняя распределения вероятностей, изображенного на рисунке 10.5а, положительна, а средняя распределения вероятностей на рисунке 10.5б отрицательна. Распределение, представленное на рисунке 10.5а характеризуется меньшей дисперсией (менее «растянуто»), чем распределение, представленное на рисунке 10.5б.

В модели средней и дисперсии относительно нее предполагается, что полезность распределения вероятностей, приносящего инвестору богатство w_s с вероятностью π_s, можно выразить как функцию средней данного распределения и дисперсии относительно этой средней: . Или, если это более удобно, полезность можно выразить как функцию средней и стандартного отклонения . Поскольку и дисперсия, и стандартное отклонение есть меры степени риска, характеризующей распределение вероятностей, можно считать полезность зависящей от любого из этих двух показателей.

Рис 10.5. Средняя и дисперсия относительно нее

Эту модель можно рассматривать как упрощение модели ожидаемой полезности, описанной в предыдущих параграфах. Если существует возможность полностью охарактеризовать варианты выбора с помощью соответствующей им средней и дисперсии относительно нее, то на основе функции полезности для средней и дисперсии можно ранжировать варианты выбора таким же образом, как и на основе функции ожидаемой полезности. Более того, даже если распределения вероятностей не могут быть полностью охарактеризованы их средними и дисперсиями, модель средней и дисперсии относительно нее может служить разумным приближением модели ожидаемой полезности.

Можно принять предпосылку о том, что при прочих равных условиях более высокий ожидаемый доход — это хорошо, а более высокая дисперсия — плохо. Это лишь другой способ сформулировать предпосылку о том, что люди обычно не расположены к риску.

Модель средней и дисперсии относительно нее можно применить к анализу задачи на структуру портфеля активов. Предположим, что у некоторого экономического агента имеется возможность инвестировать в два различных актива. Один из них - безрисковый актив, который всегда приносит постоянную норму дохода r_f. Другой актив — рисковый. Если конъюнктура фондового рынка высокая, вложение приносит высокий доход. Если конъюнктура фондового рынка низкая, это вложение приносит низкий доход. Обозначим через m_s доход на этот актив при исходе s, а через π_s – вероятность наступления такого исхода. Ожидаемый доход на рисковый актив равен r_m, а стандартное отклонение дохода на этот актив задано как σ_m.

Если доля богатства экономического агента, вложенная в рисковый актив, равна х, а доля богатства, вложенная в безрисковый актив, соответственно равняется (1 — х), то ожидаемый доход на портфель активов будет задан формулой (10.16).

(10.16)

Поскольку , получаем (10.17)

(10.17)

Таким образом, ожидаемый доход на портфель из двух активов есть среднее арифметическое взвешенное двух ожидаемых доходов.

Дисперсия портфельного дохода задана формулой (18)

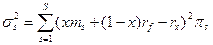(10.18)

Подставив в формулу (10.18) выражение (10.17) для r_x, получим (10.19)

(10.19)

Следовательно, стандартное отклонение портфельного дохода задано формулой (20)

(10.20)

Естественно предположить, что , так как инвестор, не расположенный к риску, никогда не будет держать в своем портфеле рисковый актив, если он приносит более низкий ожидаемый доход, чем безрисковый актив. Отсюда следует, что если индивид предпочтет направить большую долю своего богатства на покупку рискового актива, то он получит более высокий ожидаемый доход, но также будет нести и больший риск. Графическое изображение ситуации представлено на рисунке 10.10.6.

Рис. 10.6. Риск и доход

Выбрав x= 1, экономический агент вложит все свои деньги в рисковый актив и получит ожидаемый доход и стандартное отклонение вида . Выбрав x= 0, он вложит все в безрисковый актив и получит ожидаемый доход и стандартное отклонение вида . Выбрав х между 0 и 1, он окажется где-то посередине линии, соединяющей две указанные точки. Таким образом формируется линия бюджетного ограничения, описывающая предлагаемый рынком выбор между риском и доходом.

Опираясь на предпосылку о том, что предпочтения экономических агентов зависят лишь от средней и дисперсии их богатства, можно задать кривые безразличия, иллюстрирующие предпочтения индивида в отношении риска и дохода. Если люди не расположены к риску, то более высокий ожидаемый доход повышает их благосостояние, а более высокое стандартное отклонение его понижает. Это означает, что стандартное отклонение есть «антиблаго». Отсюда следует, что кривые безразличия будут иметь положительный наклон, как показано на рис. 6.

В точке оптимального выбора риска и дохода (структуры портфеля активов) наклон кривой безразличия на должен равняться наклону бюджетной линии. Этот наклон можно назвать ценой риска, так как он характеризует пропорцию, в которой могут обмениваться риск и доход при выборе оптимальной структуры портфеля.

Цена риска задается формулой (10.21).

(10.21)

Точку, описывающую оптимальную структуру портфеля можно охарактеризовать условием соблюдения равенства предельной нормы замещения дохода риском и цены риска (10.22).

(10.22)

Предположим, что существует много индивидов, производящих выбор между двумя указанными активами. Для каждого из них предельная норма замещения должна равняться цене риска. Следовательно, в ситуации равновесия предельные нормы замещения (MRS) у всех индивидов будут равны: если предоставить людям достаточно широкие возможности для торговли рисками, то равновесная цена риска для всех индивидов будет одинаковой. Риск в этом отношении ничем не отличается от других товаров.

Рассмотренная модель описывает цену риска. Однако возникает вопрос: как измеряется величина риска, характеризующего данный актив? Для рассмотренной выше ситуации, в которой существовал один рисковый актив и один безрисковый, величина риска, характеризующая рисковый актив, есть его стандартное отклонение. Однако если речь идет о нескольких рисковых активах, стандартное отклонение не является подходящей мерой величины риска, характеризующей актив. Причина этого в том, что полезность для потребителя зависит от среднего значения и дисперсии общего богатства, а не от среднего значения и дисперсии какого-то отдельного принадлежащего ему актива. Важен, характер взаимодействия доходов на различные принадлежащие потребителю активы, определяющий среднее значение и дисперсию его богатства. Курсовая стоимость данного актива определяется его предельным влиянием на общую полезность, а не стоимостью данного актива, взятой отдельно. Так, сумма, которую кто-либо готов заплатить за дополнительную акцию, дающую право владения рисковым активом, будет зависеть от того, как этот актив взаимодействует с другими активами его портфеля.

Риск по данному активу удобно измерять по отношению к риску по фондовому рынку в целом. Степень риска актива, измеренная относительно риска по рынку в целом, называется бетой актива и обозначается греческой буквой β.

Если бета данного вида акций равна 1, степень риска по ним такая же, как и по фондовому рынку в целом. Так, при росте курсов акций на фондовом рынке в среднем на 10% курс акций данного вида вырастет в среднем на 10.%. Если бета акций данного вида составляет менее 1, то при росте курсов акций на фондовом рынке в среднем на 10% курс акций данного вида вырастет менее чем на 10%. Оценку беты акций позволяют получить статистические методы, определяющие степень чувствительности движений одной переменной по отношению к движениям другой.

Дата добавления: 2014-11-18