Приклад 7.4 1 страница

Пусть изучается нормально распределенная случайная величина 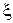с дисперсией 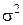. Высказывается гипотеза, что генеральное среднее этой величины 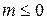(односторонняя гипотеза). Требуется проверить эту гипотезу по одному наблюдению .

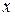Розв‘язання.

Если мы хотим, чтобы вероятность ошибки первого рода была не больше , мы должны считать гипотезу неверной только, если , где – квантиль стандартного нормального распределения. Действительно, с доверительной вероятностью справедлива односторонняя оценка 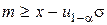, которая позволяет утверждать, что лишь при . Если окажется, что , то мы будем вынуждены рассматриваемую гипотезу признать справедливой, хотя, возможно, допустим при этом ошибку второго рода. Вероятность неравенства зависит от того, каким на самом деле является 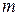. Если обозначить через 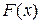функцию нормального распределения со средним 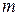и дисперсией 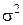, то или, используя функцию Лапласа (див. коментар до табл. Б1 у додатку Б),

. (7.9)

Если , то гипотеза неверна. Однако в принципе 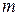может быть сколь угодно близким к нулю, а это значит, что будет сколь угодно близка к .

Вправа 7.3

Доведіть справедливість цієї рівності.

Таким образом, максимальная вероятность ошибки второго рода равна

(7.10)

Вправа 7.4

Доведіть справедливість цієї рівності.

Например, при обычном уровне значимости вероятность ошибки второго рода будет , т. е. мы почти всегда ошибемся и примем неверную гипотезу.

É

Итак, желая застраховать себя от несправедливого отклонения верной гипотезы, мы впадаем в другую крайность, объявляя правильными почти сплошь неверные гипотезы. Точно такая же картина возникнет, если в качестве отправной точки взять фиксированную малую вероятность 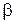. Для того чтобы вероятность принять неверную гипотезу не превышала 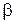, мы должны будем отклонять гипотезу уже при 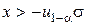. А это значит, что большой стянет вероятность , но по-прежнему равная 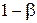. Соотношение вероятностей и 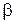наглядно представлено на рис. 7.1, где эти вероятности выражаются площадями участков под нормальной кривой. Площадь, расположенная вправо от критического значения, равна , расположенная влево равна 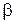. Стараясь уменьшить , мы сдвигаем это критическое значение вправо, стараясь уменьшить 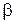– влево. Ясно, что с помощью единого критического значения невозможно даже добиться того, чтобы обе эти вероятности были меньше .

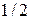На практике обычно вероятности ошибок обоих родов задаются заранее и являются малыми числами (не больше 0.1). В этом случае при проверке гипотезы приходится пользоваться одновременно двумя критическими значениями: считать гипотезу верной, если , и неверной, если .Такой подход обеспечивает заданный уровень вероятностей ошибок первого и второго рода, однако при этом появляется участок неопределенности 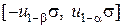. Длина этого участка

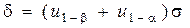(7.11)

называется неопределенностью критерия. Вопрос о том, какой вывод делать в случае, если 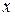попадет на участок неопределенности, решается применительно к условиям задачи; чаще всего в этом случае гипотеза объявляется сомнительной и подвергается повторному анализу.

Неопределенность критерия существенно ухудшает эффект статистического анализа гипотез. Поэтому ее всячески пытаются, если не устранить вообще (мы уже видели, что это невозможно), то по крайней мере сделать как можно меньше. Непосредственно из (7.11) следует, что это можно сделать и при неизменных заданных и 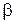, если уменьшать дисперсию .

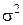Уменьшать дисперсию можно, повышая точность методики. Но более универсальным и надежным средством является увеличение числа параллельных наблюдений. Действительно, если вместо одиночного провести параллельных наблюдений и рассмотреть их среднее 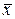, то его дисперсия . Проверяя гипотезу по значению 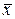, мы должны будем принять ее, если 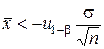, и отвергнуть, если .

Неопределенность станет теперь равной 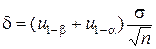, т. е. уменьшится в 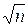раз.

В практических задачах допустимая неопределенность критерия задается обычно заранее, наряду с вероятностями и 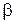. Это позволяет сразу же определить необходимое число параллельных наблюдений (повторностей):

. (7.12)

Проиллюстрируем сказанное конкретным примером.

Приклад 7.5 [20]

Лаборатория химического завода проверяет выпускаемую продукцию, чтобы содержание вредной примеси не превышало 0.04%. Ошибка воспроизводимости одиночного анализа . Требуется, чтобы вероятность пропустить бракованную продукцию не превышала . Вместе с тем анализ не должен браковать хорошую продукцию. Разумеется, если содержание примеси в продукции «на пределе», какие-либо гарантии дать трудно. Но можно, например, потребовать, чтобы вероятность забраковать продукцию с содержанием примеси ниже (достаточно хорошая продукция) не превышала . Нужно определить количество параллельных анализов , которое позволило бы удовлетворить всем поставленным требованиям.

Розв‘язання.

Чтобы использовать проведенные ранее теоретические рассуждения, будем в качестве случайной величины 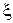рассматривать отклонение результата анализа примеси от заданного предела 0.04. Генеральное среднее 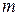величины 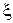даст истинное значение этого отклонения. Предположение «продукция годна» совпадает с гипотезой 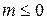. Вероятности и 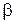заданы в явном виде, допустимую неопределенность критерия легко найти: . Отсюда согласно (7.12) находим:

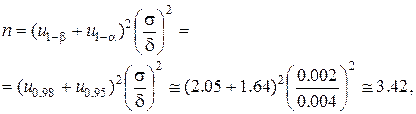
Численные значения квантилей найдем из таблицы Б1.

Вправа 7.5

Поясніть, як знайдено оцінки 2.05 і 1.64.

Таким образом для выполнения всех требований задачи нужно делать четыре анализа (повтора). Продукция будет при этом признана безоговорочно годной, если среднее отклонение по результатам этих четырех измерений будет удовлетворять условию

т. е. если по результатам четырех анализов содержание примеси (в среднем) окажется меньше 0.038%.

Если результат анализа будет больше, чем 0.038%, то продукция является или сомнительной (в пределах участка неопределенности), или бракованной. Обычно участок неопределенности присоединяют к участку непригодной продукции, считая продукцию бракованной всегда, как только результат анализа окажется больше 0.038%. Связано это с тем, что завод при выпуске продукции никогда не работает «на пределе», поэтому вероятность продукции с содержанием примеси, близким к 0.04%, достаточно мала.

É

Описанная схема анализа предполагает, что число параллельных наблюдений выбирается до опыта и в дальнейшем не меняется. Однако если бы первый же анализ из рассмотренного примера показал содержание примеси 0.02%, вряд ли стоило бы продолжать анализы. Иными словами, выбранное заранее всегда достаточно для получения заданных вероятностей и 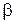, но отнюдь не всегда необходимо.

До сих пор во всех наших рассуждениях проверялась гипотеза 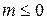. Гипотеза проверяется аналогично, только теперь ее нужно принимать, если

Обе эти гипотезы односторонние и проверяются с помощью односторонних критериев.

Если же проверяется двусторонняя гипотеза (ни больше, ни меньше), то для проверки нужно применить двусторонний критерий. Пусть, по-прежнему, вероятность отклонить верную гипотезу равна , а вероятность принять гипотезу, в то время как на самом деле , равна 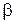. Тогда число наблюдений определяется формулой

. (7.13)

Мы рассмотрели вопрос о выборе числа параллельных наблюдений, когда дисперсия наблюдений 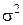известна заранее. Если же 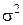заранее неизвестна, то для оценок нужно применять критерий Стьюдента. Выбор числа наблюдений при этом существенно усложняется и мы здесь такую задачу рассматривать не будем.

7.3.3. Последовательный анализ.

Число наблюдений можно сократить, если по ходу анализа учитывать уже сделанные наблюдения. Обобщением этой идеи служит разработанный Вальдом метод последовательного анализа. В этом методе после каждого нового наблюдения решают, принять гипотезу, отклонить или продолжать испытания. Последовательный анализ позволяет сокращать число необходимых наблюдений в среднем в два раза по сравнению с обычными методами, фиксирующими число наблюдений заранее.

Последовательный анализ используется при решении многих задач, в частности, статистической радиотехники. Мы рассмотрим его применение только к анализу генерального среднего 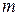наблюдаемой случайной величины. Допустим, что нам нужно сделать выбор между гипотезами и 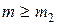(предполагается, что ). Вероятность принять гипотезу 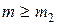, когда в действительности , это . Вероятность противоположной ошибки, т. е. 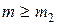принятия гипотезы , когда в действительности , это 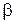. 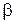Числа и обычно малы и задаются заранее.

Основная идея последовательного анализа заключается в следующем. При каждой совокупности наблюдений мы можем найти вероятность 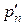того, что эти наблюдения получены из совокупности с генеральным средним и вероятность того, что они получены из совокуп­ности с генеральным средним . На практике обычно осуществляются события с максимальной вероятностью. Это значит, что при нужно считать более правдоподобным значение (а с ним и всю гипотезу ). Если же , то предпочтение нужно отдать второй гипотезе .

Итак, все определяется отношением правдоподобия , а именно, будет ли оно больше или меньше единицы. Ясно, однако, что в случае, когда отношение правдоподобия лишь немного отличается от единицы, предпочтение соответствующей гипотезе будет весьма сомнительным и лучше всего продолжить испытания. Точные показатели, насколько должно отношение правдоподобия отличаться от единицы, чтобы между гипотезами можно было сделать уверенный выбор, определяются заданными вероятностями и 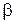. Было показано, что гипотезу можно принять, если

и гипотезу можно принять, если

Если же

,

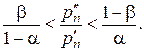то испытания надо продолжать.

При каждом новом наблюдении границы для отношения правдоподобия не меняются, меняется лишь само отношение. Это облегчает применение последовательного анализа, позволяет его свести к простым алгоритмам.

Если наблюдаемая случайная величина имеет нормальное распределение с заранее известной дисперсией 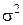, то условие продолжения испытаний можно преобразовать к виду

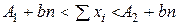, (7.14)

где

(7.15)

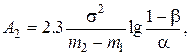(7.16)

. (7.17)

Константы и 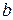подсчитываются сразу же по исходным данным, благодаря чему дальнейшая проверка ведется только по сумме проделанных наблюдений и их числу.

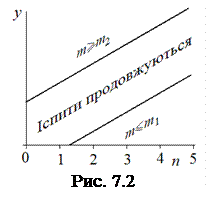Последовательный анализ нормально распределенной случайной величины особенно удобно иллюстрировать и проводить геометрически. Для этого после каждого наблюдения строят точку на координатной плоскости, откладывая по оси абсцисс число проделанных наблюдений , а по оси ординат их сумму . Испытания нужно продолжать, пока эти точки будут находиться в полосе между прямыми и (рис. 7.2). Если же хоть одна точка окажется ниже этой полосы, анализ нужно прекращать и принимать гипотезу . Точно так же гипотеза 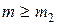принимается, как только хоть одна точка окажется выше указанной полосы.

Рассмотрим пример.

Приклад 7.6

В магазин, в лабораторию или цех партиями поступает некоторая продукция, например, резисторы. К партии предъявляются достаточно жесткие требования: количество бракованной продукции не должно превышать 5% с вероятностью 0.95, если это условие не выполняется, партия бракуется; чтобы не впадать в другую крайность – браковать хорошие изделия, ставится еще одно требование – партия, в которой бракованных изделий не больше, чем 4.5% принимается с вероятностью 0.90. Кроме того, в связи с погрешностями измерений и неоднородностью партии появляется СКО результатов, известная по большому числу предыдущих измерений равная 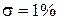. Для оценки качества партии из нее берутся пробы. Возникает вопрос: сколько проб нужно взять из партии, чтобы убедиться в том, что она удовлетворяет сформулированным требованиям. Воспользуемся методом последовательного анализа.

Розв‘язання.

Согласно условия задачи . Вероятности ошибок первого и второго рода и , соответственно.

Из того, что по условию задачи случайная величина 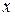характеризуется только двумя параметрам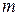и и 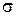, делаем вывод: случайная величина 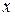подчиняется нормальному закону распределения. Следовательно, можно воспользоваться выражениями (7.14) – (7.17).

Первое, что нужно сделать, это определить область продолжения испытаний. Для этого сначала найдем константы и .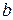

;

;

.

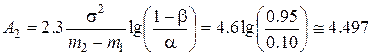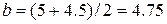Таким образом, область продолжения анализа будет ограничена прямым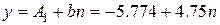и

и .

Эти прямые построены на графике рис. 7.3. Область продолжения анализа между ними выделена цветом.

Теперь можно приступить собственно к последовательному анализу.

Предположим, что анализ первой пробы из партии дал результат . Ему соответствует на рис. 7.3 точка с абсциссой и ординатой . Точка,находится в «полосе продолжения испытаний», поэтому берем 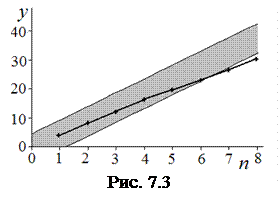вторую пробу. Ее анализ дал результат , что соответствует точке с абсциссой и ординатой . Испытания снова нужно продолжать. Третий анализ дал значение , ему соответствует точка с абсциссой и ординатой . Четвертому анализу с результатом соответствует точка . Пятая точка, соответствующая анализу с результатом 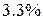, имеет координаты . Шестая проба дала результат . Координаты соответствующей точки на графике рис. 7.3 такие: 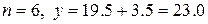. На графике рис. 7.3 эта точка, кажется, лежит на нижней границе области продолжения испытаний. Проверим это. Подставим в уравнение нижней границы 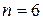и получим а Это значит, что точка с координатами 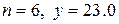принадлежит область продолжения анализа. Седьмой замер дал результат , координаты соответствующей точки таковы: . Точка с такими координатами вышла за границы области продолжения испытаний и анализ партии изделий на этом можно считать оконченным. На рис. 7.3 нанесена еще и восьмая точка (), координаты которой определены как и для предыдущих измерений. Для этого измерения соответствующая точка на графике явно находится вне области продолжения. Может показаться, что можно принять гипотезу: партия изделий является доброкачественной уже из первого анализа. К сожалению, такой вывод поспешен, так как из-за высокого значения 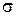мы не можем гарантировать заданные вероятности ошибок и .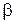

Для решения поставленной задачи с помощью метода последовательного анализа нам понадобилось семь наблюдений. Если же мы захотели бы определить число наблюдений заранее по формуле (7.12), то получили бы

Вправа 7.6

Поясніть, як знайдено оцінки квантілів і

Таким образом классический метод потребовал бы выполнения 34-х анализов, а метод последовательного анализа – только 7-ми. Преимущества последовательного анализа неоспоримы.

É

Рассмотрим простой пример, в котором продемонстрируем еще одно важное преимущество, которое обеспечивается при грамотном планировании эксперимента.

Приклад 7.7 [1]

Необходимо измерять сопротивление каждого из трех последовательно включенных резисторов .

Розв‘язання.

Если пользоваться традиционным и, казалось бы, очевидным методом, нужно измерить каждое в отдельности сопротивление и, предварительно выполнив еще одно измерение, с замкнутыми накоротко выводами измерительного прибора для установки нуля его показаний. Схему такого эксперимента, состоящего из четырех опытов, можно представить матрицей планирования , столбцы которой отражают операцию измерения сопротивлений и для общности математических выражений обозначенных 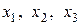.Зависимая переменная представлена вектором 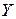. Тогда

Дата добавления: 2014-11-18