Элементы статистической обработки данных 3 страница

Абсолютная величина – количественная характеристика объема (размера) изучаемого явления в определенных временных и/или пространственных границах. Абсолютную величину получают путем суммирования статистических данных об изучаемом явлении. Абсолютная величина всегда именованное число, то есть имеет размерность, связанную с принятой единицей измерения. Отметим, что в статистике термин «абсолютная» не имеет толкования «модуль» в математике. В статистике абсолютная величина может быть и отрицательной.

Одна из основных операций при анализе статистических данных – сравнение числовых величин, характеризующих изучаемое явление. Непосредственное сравнение абсолютных величин, характеризующих это явление в различные моменты времени или в разных точках пространства, не всегда приводит к верным выводам (см. табл. 2.3 ниже). Более продуктивным оказывается сравнение относительных величин.

Относительная величина – количественная мера соотношения двух абсолютных величин, одна из которых принимается за базу сравнения. Вычисляют относительную величину путем деления сравниваемой абсолютной величины на базу сравнения. Ниже рассматриваем только отношение абсолютных величин, имеющих одну и ту же размерность. Полученная так относительная величина характеризует распределение исследуемого явления в пространстве или развитие его во времени.

В тех случаях, когда модуль отношения абсолютных величин лежит в пределах [»0.001,»3], относительную величину удобно выражать в процентах. Для этого базе сравнения B ставят в соответствие 100%, а сравниваемой абсолютной величине A отвечают A%. Так составляют пропорцию

= ,

которая лежит в основе всех операций с процентами.

Когда заданы величины A и В, то A% вычисляют так:

A%= %. (2.3)

Пример. По данным Федеральной службы государственной статистики за 2009 год составлена табл. 2.3.

Сравнение абсолютных величин П приводит к выводу о том, что положение с преступностью в Тульской обл. хуже, чем в Тамбовской. Однако сравнение относительных величин П%, полученных по формуле (2.3), дает противоположный результат, который и отвечает фактическому состоянию преступности в этих регионах.

Таблица 2.3
Регион	П – число лиц, совершивших преступления (тыс. чел)	Н – население (тыс. чел)	П%=
Тамбовская обл.	9.22	1088.44	0.85%
Тульская обл.	9.54	1540.38	0.62%

Когда же заданы значения A% и В, величину A находят так:

A=B´ . (2.4)

Пример. В 2009 году число лиц (тыс.), совершивших преступления в России, оказалось равным 1219.8. Из них 15.9% – женщины. Абсолютное число женщин найдем по формуле (2.4):

женщины: =193.9.

А если заданы A и A%, то базу B находят по формуле

B=A´ . (2.5)

Пример. В 2009 году в РФ осуждено лиц (тыс.) 892.2, что составило 73.1% от числа лиц, совершивших преступления в России в этом же году. По формуле (2.5) найдем число лиц, совершивших преступления в России в 2009 году:

892.2´ =1220.5.

Полученный результат 1220.5¹1219.8 (см. выше) обусловлен погрешностями округления и абсолютных, и относительных величин.

Рассмотрим еще две относительные величины, которые характеризуют развитие изучаемого явления в заданном временном интервале и которые тоже выражаются в процентах. В этом случае задана таблица, в первой строке которой приведены отсчеты времени T_i (месяцы, годы), а во второй – значения абсолютных величин A_i в эти моменты времени (i= 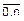). Тогда динамика развития исследуемого явления на интервале от T₀ до T_n характеризуется его темпом роста и темпом прироста.

Темп роста ТР_i – выраженное в процентах отношение абсолютной величины A_i в данный момент к базовой величине A_Б:

ТР_i= , i= .

Темп прироста ТП_i – выраженное в процентах отношение разности абсолютной величины в данный момент времени и базовой величины A_i-A_Б к базовой величине A_Б:

ТП_i= =ТР_i-100%, i= .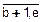

Как видим, ТП_i=0 при ТР_i=100%, то есть начало отсчетов ТП_i сдвинуто относительно относительнотначала отсчетов ТР_i на 100. При этом типовым значениям ТР=80..120 отвечают меньшие значения ТП=-20..20. Поэтому достаточно вычислять только значения ТП_j.

Применяют два способа вычисления названных показателей динамики: базисный и цепной. Различаются они заданием базовой величины A_Б.

Базисный способ. В этом случае величина A_Б одна и та же для всех моментов времени. Обычно в качестве базы выступает значение абсолютной величины в начальный момент времени: A_Б=A_b. Тогда базисным способом темп прироста ТПБ_i вычисляют так:

ТПБ_i= 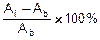, i= .

Таким образом, ТПБ_i характеризует относительное изменение величины A за период от начального момента времени b до текущего значения i.

Цепной способ. В этом случае величина A_Б – переменная. Для данного момента времени она равна значению абсолютной величины в предыдущий момент времени: A_Б=A_i-1. Тогда цепным способом темп прироста ТПЦ_i вычисляют так:

ТПЦ_i= , i= .

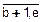Таким образом, ТПЦ_i характеризует относительное изменение величины A за единицу времени i.

Пример. В табл. 2.4 приведены темпы прироста числа таких преступлений в РФ за 2008-2012 годы, как взяточничество, вычисленные базисным и цепным способами.

Таблица 2.4
i
Ai
ТПБi%		+05.03	-04.00	-12.47	-22.01
ТПЦi%	-	+05.03	-08.59	-08.82	-10.90

Как видим, с 2008 года по 2009 годколичество таких преступлений как взяточничество в РФ выросло на 5.03%. С 2008 года по 2010 год эта число уменьшилось на 4%. А с 2008 года по 2012 год (за четыре года) оно снизилось на 22.01%.

За один год с 2008 по 2009 год количество таких преступлений как взяточничество в РФ выросло на 5.03 процента. А в 2010-2011 годах оно уменьшалось примерно на 9% за один год. За 2012 год это число снизилось примерно на 11%.

2.4. Алгоритмы решения вычислительных задач

Приступая к решению любой задачи, человек планирует последовательность действий, выполнение которых приводит к достижению поставленной цели. Подобный план действий называют алгоритмом. Вообще человек живет в мире алгоритмов. Так, имея намерение позвонить в другой город, мы в кабине междугороднего телефона находим инструкцию, следуя которой можно это сделать. Своего рода сборником алгоритмов является УПК (скажем, Глава 26. Допрос. Очная ставка. Опознание. Проверка показаний). Но все такого рода алгоритмы не являются предметом нашего внимания. В математике имеют дело с вычислительными алгоритмами.

Вычислительным алгоритмом называется строгое описание эффективной процедуры решения математической задачи.

Конечно, такое определение алгоритма отнюдь не научное. Не ясно, что значит «строгое описание» или «эффективная процедура». Но интуитивно понятно, что здесь имеется в виду. И нам этого вполне достаточно.

Поясним смысл сказанного примером. Пусть заданы натуральные числа A и B. Требуется найти их наибольший общий делитель НОД. Древнегреческий математик Евклид в III веке до н.э. составил остроумный алгоритм решения этой задачи. Приведем описание этого алгоритма в современной интерпретации:

0. Положить X равным A, а Y равным B.

1. Если X больше Y, то перейти к п.4.

2. Если X меньше Y, то перейти к п.5.

3. Положить НОД равным X и перейти к п.6.

4. Положить X равным X-Y и перейти к п.1.

5. Положить Y равным Y-X и перейти к п.1.

6. Закончить вычисления (СТОП).

Таблица 2.5
Шаг	Пункт алгоритма	Результат действия
		X=12, Y=18.
		X>Y? – Нет.
		X<Y? – Да.
		Y=Y-X=6.
		X>Y? – Да.
		X=X-Y=6.
		X>Y? – Нет.
		X<Y? – Нет.
		НОД=6.
		СТОП.

Проверим работу этого алгоритма на примере. Пусть A=12 и B=18. Наши действия по реализации алгоритма сведем в табл.2.5 Как видим, процедура вычислений, порождаемая алгоритмом, представляет собою последовательность шагов. На каждом шаге выполняется тот или иной пункт из описания алгоритма.

Назовем основные требования, которым должны отвечать алгоритмы.

1. Конечность. Это требование состоит в том, что запущенный в работу алгоритм за конечное число шагов должен завершиться получением искомого результата.

2. Определенность. На любом шаге вычислений должно быть ясно, что делать дальше (перейти к следующему пункту, вернуться к тому или иному из предыдущих пунктов, или закончить работу).

Каждому алгоритму ставится в соответствие множество числовых величин, допустимых для него в качестве исходных данных. Точно так определено и множество допустимых для этого алгоритма результатов вычислений. Скажем, для алгоритма Евклида исходные величины А и В, результат его работы НОД относятся к классу натуральных чисел. Применение алгоритма к величинам, которые не являются для него допустимыми, чревато, как минимум, получением абсурдных результатов, но, скорее всего, алгоритм на этих данных не будет отвечать требованиям конечности и определенности. В этом убеждает применение алгоритма Евклида к отрицательным целым числам.

Алгоритм Евклида был задан своим словесным описанием. Ясно, что так можно описать решение сравнительно простой задачи. Более или менее сложная задача потребует громоздкого, запутанного словесного описания. И все равно, в самом подробном таком описании многое останется между строк, в контексте. Например, в алгоритме Евклида мы не указали явно, что после пункта 0 должен выполняться пункт 1, а при невыполнении условия X больше Y в пункте 1 следует перейти к пункту 2. Все это – нарушение требования определенности алгоритма. В естественном языке имеются синонимы, а есть и многозначные слова. Поэтому получить строгое задание алгоритма средствами естественного языка нельзя.

Рассмотрим самый удобный и наглядный способ задания алгоритмов, свободный от указанных недостатков словесного описания. Это представление его в форме графа алгоритма. Так, на рис.2.3 показан граф алгоритма вычисления НОД по Евклиду. Сравнив рис 2.3 с вербальным описанием этого алгоритма, легко убедиться в том, что они практически идентичны. Отметим, кстати, что такое указание вербального алгоритма как «Положить X=X-Y!» на графе задается конструкцией: X:=X-Y, которую называют оператором присваивания.

Опишем подробнее средства графического представления алгоритмов.

На том или ином шаге вычислений выполняют действия двух типов. Первый тип действий – содержательная обработка информации: задание исходных данных, вычисление значения переменной, (например, Y:=Y-X), фиксация результатов вычислений и т.п. Второй тип действий – анализ результатов, полученных на предыдущих шагах, и выбор дальнейшего пути развития вычислительного процесса (скажем, проверка условия X>Y и переход по результату проверки на тот или иной пункт алгоритма). В соответствии с этим, для графического представления алгоритмов используем двасимвола:

ü прямоугольник, внутри которого записывается действие первого типа, выполняемое на данном шаге вычислений,

ü ромб (или шестиугольник, полученный усечением ромба, как на рис.2.3), внутри которого записывается проверяемое условие.

Эти символы называют вершинами графа: прямоугольник – операторной вершиной, а ромб (шестиугольник) – условной вершиной.

Вершины графа соединяют дугами (стрелками) в соответствии с логикой развития вычислительного процесса.

Операторная вершина может иметь один или несколько входов (к ней подходят одна или несколько стрелок), но у нее должен быть один и только один выход (из нее выходит лишь одна стрелка).

Условная вершина, как и операторная, может иметь один или несколько входов. Проверяемое условие в момент его проверки может выполняться (да), а может и не выполняться (нет). Поэтому условная вершина имеет два выхода. Один из них отвечает тому направлению хода вычислений, которое имеет место при выполнении условия. Этот выход отмечается символом 1. Второй выход соответствует тому направлению развития вычислительного процесса, которое имеет место, когда условие в ромбе не выполняется. Этот выход отмечается символом 0.

Среди операторных вершин две – особые: начальная и конечная. Начальная вершина не имеет входов, конечная вершина не имеет выхода. На рис. 2.3. начальная вершина – Ввод X,Y, а конечная – Вывод НОД.

Корректно разработанный граф (тот, который отвечает требованиям конечности и определенности) отличается тем, что:

ü он должен иметь одну и только одну начальную вершину, одну и только одну конечную вершину,

ü из любой вершины графа должен быть путь в конечную вершину.

Для того чтобы в поясняющем тексте можно было сослаться на ту или иную вершину графа, ее снабжают меткой. Обычно в качестве метки используют число, записываемое в разрыв контура вершины. На рис. 2.3 вершины графа отмечены символами, которые отвечают пунктам словесного алгоритма Евклида.

Вопросы и задачи для самоконтроля

1. Определить понятие «позиционная система счисления».

2. Выполнить последовательный перевод из десятичной системы счисления в двоичную, а из нее в шестнадцатеричную, после чего вернуться в десятичную для чисел:

130, 251, 617, 976, 1920, 5295, 12908.

3. С какими классами чисел оперируют на практике и в математике? Дать характеристику каждому из классов чисел и отношениям между классами.

4. Пояснить смысл операции (A)_{mod M}. Найти (A)_{mod M} для

A={1000, 73,7} и M={19, 10, 6}.

5. Сформулировать алгоритм округления десятичных дробей. Округлить число

p=3.14159265358979323846264338327950

до шести, до двух знаков, до целого.

6. Разработать граф алгоритма округления правильной дроби до k разрядов после точки.

7. Представить в стандартной форме числа

0.000765402, 76540.2

Таблица 2.6
город	по штату	некомплект
Гончаров
Тургенев

8. Данные о количестве судей в городах Гончаров и Тургенев сведены в табл. 2.6. В каком из городов ситуация с судьями сложнее?

9. Выполнить ДКЗ: Тест 2. ЧИСЛА.

Глава 3. ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ

3.1. Понятие высказывания

Математическая логика – это теория верных рассуждений. При этом абсолютно безразлично, к какой области эти рассуждения относятся. Цепочка рассуждений, относящихся к той или иной области, описывается на языке математической (формальной) логики, а затем проверяется их верность или ошибочность. Такая универсальность законов математической логики обусловила ее широкое применение, как в технических, так и в гуманитарных науках. Она составляет теоретический фундамент построения и функционирования компьютеров, ее методы активно используются в экономике, медицине, психологии, языкознании и др.

Основное понятие математической логики – высказывание (утверждение). Это понятие средствами математической логики не определяется. Основной признак высказывания: оно может быть или истинным, или ложным. При этом высказывание не может быть и истинным, и ложным одновременно. Говорят, что истина или ложь – возможные значения каждого из высказываний. Для примера приведем такие высказывания из разных областей:

Математика – это круто!

H₂O – формула этилового спирта.

Если новый уголовный закон смягчает наказание за деяние, которое отбывается лицом, то это наказание подлежит сокращению в пределах, предусмотренных новым уголовным законом (УК РФ, ст. 10, ч. 2).

Не являются высказываниями фразы типа: «Любовь есть предисловие к разлуке» (И. Бродский), «Зри в корень!» (Козьма Прутков), «Разрешите выйти?» (студент первого курса). Про каждую из них нельзя сказать, истинна она или ложна.

Очевидно, что существуют высказывания простые и сложные. Сложное высказывание можно разложить на простые. Из приведенных выше высказываний первые два – простые, а в третьем можно выделить такие простые высказывания:

§ новый уголовный закон смягчает наказание за деяние, которое отбывается лицом,

§ наказание подлежит сокращению в пределах, предусмотренных новым уголовным законом.

Простым называют такое высказывание, никакая часть которого высказыванием уже не является.

Начало науки о законах и формах мышления – логики связывают с именем Аристотеля (IV в. до н.э.). В XVII в. Г. Лейбниц (юрист, напомним) ввел в логику математическую символику и использовал ее для общих логических построений, то есть положил начало формализации логики. В XIX в. Дж. Буль последовательно реализовал идеи Г. Лейбница, первым исследовал алгебраические свойства высказываний, тем самым заложил основы математической логики. Поэтому математическую логику нередко называют булевой алгеброй или алгеброй логики.

3.2. Операции над высказываниями

Простые высказывания в булевой алгебре называют логическими переменными. Мы их будем обозначать как x_m-1, x_m-2,¼, x₀. Логическая переменная может принимать одно из двух значений: или истина, или ложь. Удобно значение истина обозначить символом 1, а значение ложь – символом 0. В булевой алгебре над логическими переменными выполняют логические операции. Результат любой логической операции – сложное высказывание. Это сложное высказывание обозначим как Y.

Каждая логическая операция задается своей таблицей, которая называется таблицей истинности (табл. 3.1). Входами таблицы являются наборы значений всех логических переменных – операндов данной логической операции x_m-1, x_m-2,¼, x₀ в каждой строке таблицы, а выходом – результат этой логической операции Y.

	Таблица 3.1
a	xm-1	¼	x1	x0	Y
		¼
		¼
		¼
		¼
¼	¼	¼	¼	¼	¼
k		¼
¼	¼	¼	¼	¼	¼
2^m-2
2^m-1		¼

Таблица истинности для m переменных будет иметь 2^m строк для всех комбинаций (наборов), составляющих значения этих переменных. При ее заполнении нужно ни один из наборов и не пропустить, и не повторить. Существует простое правило заполнения таблицы наборами значений переменных. Оно основано на том факте, что любая из логических переменных в половине из 2^m строк своего столбца имеет значение 0, а на другой половине – значение 1. Распределение нулей и единиц в каждом столбце – свое. Итак, начинаем заполнять столбцы. Самый правый столбец для x₀ заполняем сверху вниз последовательностью нуль, один, нуль, один и т.д. до единицы в последней строке таблицы. Столбец для x₁ заполняем последовательностью два нуля, две единицы, колонку для x₂ – последовательностью четыре нуля, четыре единицы. Продолжаем эту процедуру: серии из нулей и единиц в каждом следующем столбце вдвое больше, чем в предыдущем. В самой левой колонке для x_m-1 первая половина ячеек будут заполнены нулями, а вторая – единицами. При этом самая первая строка аргументов будет заполнена нулями (все нули), а последняя – единицами (все единицы), и ни один из наборов не будет пропущен и не будет повторен! Заполнив ячейки для логических переменных, заполняют столбец для Y его значениями на каждом из наборов.

Пронумеруем строки таблицы a= . Тогда двоичная m-разрядная запись номера строки совпадает с набором нулей и единиц в этой строке.

Рассмотрим основные логические операции.

Таблица 3.2
x	Y

Отрицание. Отрицание – операция одноместная. Отрицать можно только одно высказывание. Если аргументом в операции отрицания будет логическая переменная x, а результатом Y, то эта операция задается табл.3.2. Как видим, значения x и Y взаимно обратны. Поэтому для отрицания используют название инверсия (от англ. inverse – противоположность).

Операцию отрицания записывают так:

Y=ùx,

которое читается так: Y есть НЕ x. Поэтому отрицание называют еще и операцией НЕ.

Пример. Пусть x – утверждение:

«Математика юристам необходима».

Тогда инверсией ùx этого высказывания будет фраза:

«Неправда, что математика юристам необходима».

Конъюнкция. Конъюнкция – многоместная операция. Для двух логических переменных x₁ и x₀ она задается табл.3.3. Как видим,

конъюнкция истинна, когда все ее аргументы истинны,

конъюнкция ложна, когда хотя бы один из ее аргументов ложен.

Таблица 3.3
x1	x0	Y

Другими словами, Y=1 только тогда, когда И x₁=1, И x₀=1. Поэтому конъюнкцию называют операцией И. Обозначают конъюнкцию символом Ù:

Y=x₁Ùx₀.

Результат конъюнкции совпадает с результатом умножения чисел 1 и 0. Поэтому ее называют еще и логическим умножением.

Пример. Пусть x₁ – утверждение:

«Двенадцать делится на три»,

а x₀ – высказывание:

«Двенадцать делится на четыре».

Их конъюнкцией x₁Ùx₀ будет высказывание:

«Двенадцать делится на три и на четыре».

Конъюнкция n переменных записывается так:

Y=x_n-1Ùx_n-2Ù¼Ùx₀.

Дизъюнкция. Дизъюнкция – тоже многоместная операция. Для двух логических переменных x₁ и x₀ она задается табл.3.4. Как видим,

дизъюнкция ложна, когда все ее аргументы ложны,

дизъюнкция истинна, когда хотя бы один из ее аргументов истинен.

Таблица 3.4
x1	x0	Y

Другими словами, Y=1 тогда, когда ИЛИ x₁=1, ИЛИ x₀=1, ИЛИ оба аргумента равны 1 (когда хотя бы один из аргументов равен 1). Поэтому дизъюнкцию называют операцией ИЛИ. Для обозначения дизъюнкции применяют символ Ú:

Y=x₁Úx₀.

Результат дизъюнкции в табл.3.4, исключая последнюю строку, совпадает с результатом сложения чисел 0 и 1. Поэтому ее называют еще логическим сложением.

Пример. Пусть x₁ – недобросовестный конкурент причинил убытки другому хозяйствующему субъекту, x₀ – он нанес ущерб его деловой репутации. Тогда x₁Úx₀ – это или действие x₁, или действие x₀, или и то и другое вместе (и все они регулируются ст. 4 Закона о защите конкуренции).

Дизъюнкция n переменных записывается так:

Y=x_n-1Úx_n-2Ú¼Úx₀.

Результатом любой из рассмотренных логических операций может быть или 0, или 1. Значит, результат одной логической операции может выступать операндом в другой. Так можно составить суперпозиции логических операций (формулы алгебры логики ФАЛ) и из простых высказываний составлять сложные. При этом следует руководствоваться правилом о приоритетах логических операций. Эти приоритеты убывают в таком порядке: НЕ, И, ИЛИ, а требуемый порядок вычислений, нарушающий правило о приоритетах, задают скобками. Правило о приоритетах логических операций позволяет сложную ФАЛ представить цепочкой простых формул.

Пример.

Y=ù((x₁Úùx₀)Ù(ùx₁Úx₀)).

P=x₁Úùx₀, Q=ùx₁Úx₀, R=PÙQ, Y=ùR.

Теперь легко составить таблицу истинности для Y (табл.3.5).

Таблица 3.5
x1	x0	ùx0	ùx1	P	R	Y

Отрицание, конъюнкция и дизъюнкция образуют функционально полную систему операций математической логики.

Дата добавления: 2014-11-18