
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Элементы статистической обработки данных 6 страница
|
|
|
|
Рассмотрим некоторые частные случаи.
v Имеем f(x)= 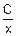 .
.
Требуется вычислить 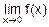 .
.
Пусть, x>0. Прямая подстановка x=0 в f(x) дает результат f(0)= 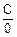 ! Если же вычислять этот предел по определению, то картина будет такой: x®0, то есть x неограниченно уменьшается, поэтому f(x) неограниченно возрастает, а именно, f(x)®¥. Значит,
! Если же вычислять этот предел по определению, то картина будет такой: x®0, то есть x неограниченно уменьшается, поэтому f(x) неограниченно возрастает, а именно, f(x)®¥. Значит, 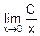 =¥. Поэтому полученный ранее результат прямой подстановки толкуется так:
=¥. Поэтому полученный ранее результат прямой подстановки толкуется так:
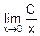 =
= 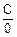 !=¥.
!=¥.
Если же, x<0, то такие же рассуждения приводят к тому, что
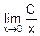 =
= 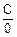 !=-¥.
!=-¥.
Заметим, что делить нельзя на точный (!) нуль. А мы здесь и не делим на нуль.
Требуется вычислить 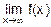 .
.
В этом случае результат прямой подстановки толкуется так:
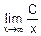 =
= 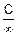 !=0.
!=0.
v Пусть функции g(x) и h(x) таковы, что и 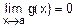 , и
, и 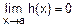 . Требуется вычислить
. Требуется вычислить 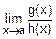 .
.
Прямая подстановка x=a дает результат 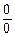 , который называют неопределенностью вида
, который называют неопределенностью вида 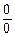 , поскольку и в числителе, и в знаменателе величины сколь угодно близкие к нулю, но не обязательно равные нулю. В этом случае нужно раскрыть неопределенность
, поскольку и в числителе, и в знаменателе величины сколь угодно близкие к нулю, но не обязательно равные нулю. В этом случае нужно раскрыть неопределенность 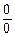 , а именно, выполнить преобразования выражений для g(x) и h(x), и вычислить предел от отношения результатов этого преобразования.
, а именно, выполнить преобразования выражений для g(x) и h(x), и вычислить предел от отношения результатов этого преобразования.
Положим, например, что g(x) и h(x) – полиномы степеней x:
g(x)=an´xn+an-1´xn-1+¼+a0, h(x)=bm´xm+bm-1´xm,-1+¼+b0.
Тогда каждый из полиномов g(x) и h(x) следует разложить на множители. Один из этих множителей и в разложении g(x), и в разложении h(x) обязательно равен (x-a). Поэтому числитель и знаменатель 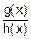 сократится на (x-a). Результатом будет новая дробь
сократится на (x-a). Результатом будет новая дробь 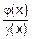 , и остается вычислить предел
, и остается вычислить предел 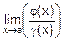 прямой подстановкой.
прямой подстановкой.
 Пример. Вычислим
Пример. Вычислим
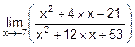 =
= 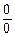 !=
!=
= 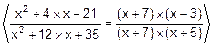 =
= 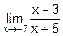 =5.
=5.
v Во многих случаях функция f(x) под знаком предела – рациональная дробь 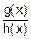 , у которой g(x) и h(x) – полиномы степеней x. Вычислим предел этой рациональной дроби при x®¥:
, у которой g(x) и h(x) – полиномы степеней x. Вычислим предел этой рациональной дроби при x®¥:
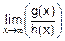 =
= 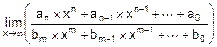 .
.
Прямая подстановка дает неопределенность вида 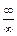 . Раскрывают ее так: в числителе выносят за скобки xn, а в знаменателе xm:
. Раскрывают ее так: в числителе выносят за скобки xn, а в знаменателе xm:
|
|
|
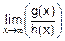 =
= 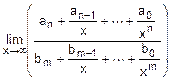 ´
´ 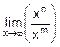 .
.
Первый из этих пределов вычисляют прямой подстановкой:
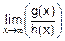 =
= 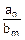 ´
´ 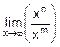 =
= 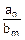 ´
´ 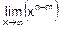 .
.
А второй предел вычисляют по результатам анализа всех возможных отношений между n и m:
при n<m получим n-m<0 и 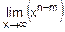 =
= 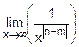 =0,
=0,
при n=m получим n-m=0 и 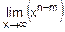 =
= 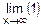 =1,
=1,
при n>m получим n-m>0 и 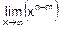 =¥.
=¥.
Изложенное позволяет найти искомый предел прямо по результатам анализа возможных отношений между n и m.
· При n<m 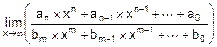 =0.
=0.
Например, 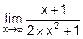 = á n=1, m=2, n<m ñ =0.
= á n=1, m=2, n<m ñ =0.
· При n=m 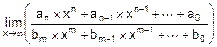 =
= 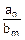 .
.
Например, 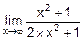 = á n=2, m=2, n=m, an=1, bm=2 ñ =
= á n=2, m=2, n=m, an=1, bm=2 ñ = 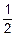 .
.
· При n>m 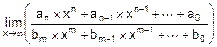 =¥.
=¥.
Например, 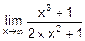 = á n=3, m=2, n>m ñ =¥.
= á n=3, m=2, n>m ñ =¥.
Вычислим предел рациональной дроби 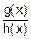 при x®-¥.
при x®-¥.
Укажем сразу, что
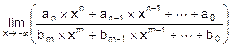
при n<m и при n=m вычисляется по тем же правилам, что и для x®+¥.
· А при n>m для x®-¥ получим
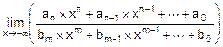 =
=
= 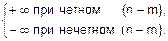
Например, 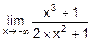 = á n=3, m=2, n>m, n-m=1, нечет. ñ =-¥.
= á n=3, m=2, n>m, n-m=1, нечет. ñ =-¥.
В теории пределов обязательно рассматривают два предела, называемых замечательными:
§ первый замечательный предел 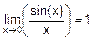 ,
,
§ второй замечательный предел 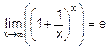 .
.
Внимание к этим пределам объясняется, в первую очередь, красотой и изяществом их доказательств (которые мы здесь, к сожалению, вынуждены опустить), а также тем, что с их помощью отыскиваются многие другие пределы.
 Пример. Во времена расцвета в России финансовых пирамид концерн «Бетти» принимал вклады на три месяца под 100% (то есть обещал удвоить сумму вклада за три месяца). А при вкладе на 1.5 месяца ставка уменьшалась до 50%, при вкладе на три недели – до 25%, то есть при уменьшении срока вклада в n раз во столько же раз уменьшается и ставка. Отсюда следовало, что нужно положить деньги, скажем, на четверть срока, по истечении которого снять уже
Пример. Во времена расцвета в России финансовых пирамид концерн «Бетти» принимал вклады на три месяца под 100% (то есть обещал удвоить сумму вклада за три месяца). А при вкладе на 1.5 месяца ставка уменьшалась до 50%, при вкладе на три недели – до 25%, то есть при уменьшении срока вклада в n раз во столько же раз уменьшается и ставка. Отсюда следовало, что нужно положить деньги, скажем, на четверть срока, по истечении которого снять уже 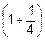 от вложенного, снова положить все деньги на четверть срока и т.д. Тогда за три месяца первоначальная сумма увеличится в
от вложенного, снова положить все деньги на четверть срока и т.д. Тогда за три месяца первоначальная сумма увеличится в 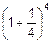 @2.44 раза. Если же описанную процедуру повторять вдвое чаще, то сумма первоначального вклада за три месяца увеличится уже в
@2.44 раза. Если же описанную процедуру повторять вдвое чаще, то сумма первоначального вклада за три месяца увеличится уже в 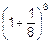 @2.57 раза.
@2.57 раза.
Найдем теоретический предел увеличения начального вклада. Последовательность 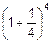 ,
, 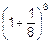 ,
, 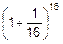 наводит на мысль о том, что при разбиении трехмесячного срока на n частей получим
наводит на мысль о том, что при разбиении трехмесячного срока на n частей получим 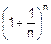 . А теперь устремим n к бесконечности:
. А теперь устремим n к бесконечности:
|
|
|
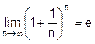 =2.72.
=2.72.
Как видим, сложные проценты привели нас к числу e – основанию натуральных логарифмов.
Вопросы и задачи для самоконтроля
1. Определить понятие «функция». Какие бывают способы задания функций?
2. Построить графики функций:
а) y=e-x, x³0; б) y1=(x-1)2, y2=x2-1, xÎR.
3. Пояснить понятие «обратная функция». Как изобразить прямую и обратную функции в одной системе координат?
4. Найти функцию, обратную к y=2-x. Построить графики прямой и обратной функций в одной системе координат.
5. Пояснить понятие «сложная функция».
6. Записать h(x)=f(g(x)) для:
а) f(s)= 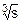 , s=g(x)=x2; б) f(s)=es, s=g(x)=sin(x).
, s=g(x)=x2; б) f(s)=es, s=g(x)=sin(x).
Построить графики каждой из сложных функций h(x).
7. Выделить вложенную и внешнюю функции
а) h(x)= 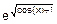 ; б) h(x)=
; б) h(x)= 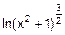 .
.
8. Пояснить смысл и назначение процедуры аппроксимации табличных функций. Привести формулы линейной аппроксимации табличной функции и пояснить процедуру их применения.
9. Зависимость количества D дорожных происшествий со смертельным исходом в год от числа v автомобилей на одну тысячу населения описывается соотношением вида
D(v)= 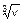 . (ДП)
. (ДП)
Построить таблицу по формуле (ДП) на отрезке [a,b], a=40, b=200, n=4.
Выполнить линейную аппроксимацию этой таблицы и найти значения D для v1=20, v2=100 и v3=240 по аппроксимирующим формулам.
Оценить погрешность аппроксимации.
10. Дать определение пределу функции. Пояснить вычисление предела путем прямой подстановки. Перечислить возможные результаты прямой подстановки.
11. Перечислить свойства пределов.
12. Пояснить, когда возникает и как раскрывается неопределенность вида 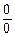 .
.
13. Пояснить, как вычисляют предел от отношения полиномов при x, стремящемся к ¥, к -¥.
14. Записать определение для каждого из замечательных пределов.
15. Вычислить:
а) 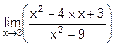 ; б)
; б) 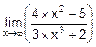 ; в)
; в) 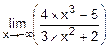 ;
;
г) 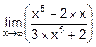 ; д)
; д) 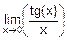 ; е)
; е) 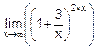 .
.
16. Выполнить ДКЗ: Тест 4. ФУНКЦИИ.
Глава 5. ОСНОВЫ ДИФФЕРЕНЦИАЛЬНОГО ИСЧИСЛЕНИЯ
5.1. Производная функции
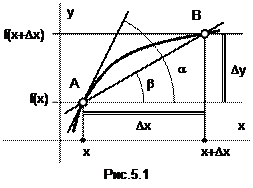
Пусть дана функция y=f(x) (рис.5.1). Зафиксируем некоторую точку x из области определения Df этой функции. А другая точка x+Dx отстоит от x на величину Dx. Величина Dx называется приращением аргумента, а разность Dy=f(x+Dx)-f(x) – приращением функции.
|
|
|
Производная функции y=f(x) в точке x – это предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
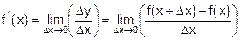 . (5.1)
. (5.1)
Поскольку y=f(x), производную f’(x) обозначают еще и как y’.
Процесс вычисления производной от функции f(x) называется ее дифференцированием.
Рис.5.1 поясняет геометрический смысл производной. Отношение 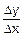 есть тангенс угла b наклона секущей AB к оси 0x. Если теперь устремить Dx к нулю, то точка B на кривой f(x) станет приближаться к точке A, угол b устремится к значению a. А a есть угол наклона касательной к кривой f(x) в точке A. Значит, производная от f(x) в точке x – это тангенс угла наклона (или угловой коэффициент) касательной к кривой f(x) в точке с абсциссой x:
есть тангенс угла b наклона секущей AB к оси 0x. Если теперь устремить Dx к нулю, то точка B на кривой f(x) станет приближаться к точке A, угол b устремится к значению a. А a есть угол наклона касательной к кривой f(x) в точке A. Значит, производная от f(x) в точке x – это тангенс угла наклона (или угловой коэффициент) касательной к кривой f(x) в точке с абсциссой x:
f’(x)=tg(a).
Производная имеет и физическое толкование, механический смысл. Исаак Ньютон нашел определение для мгновенной скорости тела, которое движется прямолинейно, но не равномерно (так, как двигался камень, отвесно брошенный Галилеем с вершины Пизанской башни). Пусть к моменту времени t тело прошло путь s(t), а к моменту t+Dt – путь s(t+Dt). Тогда средняя скорость тела на отрезке времени [t, t+Dt] будет такой:
vср= 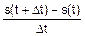 .
.
Если теперь устремить Dt к нулю, то пределом для vср и будет мгновенная скорость v(t) тела в момент времени t:
v(t)= 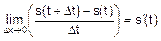 .
.
Значит, с физической точки зрения f’(x) – это мгновенная скорость изменения функции f(x) вблизи точки x.
Механический смысл производной иллюстрирует тот важный факт, что для функции y=f(x), у которой y и x являются размерными величинами, размерность производной есть размерность y, деленная на размерность x (например, размерность скорости есть м/с или км/час).
Для произвольной точки xÎDf производная f’(x) сама является функцией от x, и ее можно продифференцировать:
(f’(x))’=f’’).
Получим производную от f(x) второго порядка – ускорение функции f(x) вблизи точки x. Вторая производная тоже есть функция от x. Продолжая этот процесс, найдем f(n)(x) – производную от f(x) n-го порядка. Если все n производных от f(x) существуют, то говорят, что f(x) дифференцируема n раз. Но для любого n
f(n)(x)= 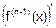 ,
,
то есть производная f(n)(x) порядка n – это первая производная от производной (n-1)-го порядка f(n-1)(x), поэтому достаточно изучить подробно производную первого порядка f’(x).
|
|
|
Правила вычисления производной базируются на следующих свойствах производных (которые, в свою очередь, основаны на свойствах пределов, поскольку производная определена через предел).
1. Если C,D=const, то
(C´f(x)+D´g(x))’=(C´f(x))’+(D´g(x))’=C´f’(x)+D´g’(x)
(производная суммы есть сумма производных, константу можно выносить за знак производной).
2. Производная от произведения функций:
(f(x)´g(x))’=f’(x)´g(x)+f(x)´g’(x).
3. Производная от отношения функций:
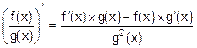 .
.
4. Производная сложной функции f(s(x))=f(s):
(f(s(x)))’=f’(s)´s’(x)= 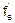 ´
´ 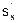
(производная сложной функции f(s) есть произведение производной внешней функции f по аргументу s на производную вложенной функции s по аргументу x).
5. Производная от обратной функции:
g’(x)= 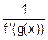 .
.
Здесь предполагается, что f(x) – прямая функция, а g(x) – обратная, и производная от прямой функции f’(x) существует.
Все свойства доказываются с использованием определения производной (5.1) и уже доказанных ранее свойств. Докажем, к примеру, свойство 5, полагая, что все предыдущие свойства уже доказаны. Пусть прямая функция есть f(x), а обратная ей – функция g(x). Если они представлены в одной системе координат, то имеет место такое равенство:
f(g(x))=x, (5.2)
(например, f(x)=x2, а g(x)= 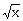 , и f(g(x))=(
, и f(g(x))=(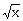 )2=x).
)2=x).
Возьмем производные от левой и правой частей равенства (5.2). При этом левую часть дифференцируем с использованием правила 4:
f’(g(x))´g’(x)=1.
Отсюда
g’(x)= 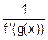 .
.
Например, для f(x)=x2 и g(x)= 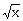 имеем:
имеем:
f’(x)= 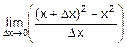 =2´x,
=2´x,
значит,
| Таблица 5.1 | |
| a) | (C)’=0, C=const |
| b) | (xp)’=xp-1´p |
| c) | (ln(x))’=  , x>0! , x>0!
|
| d) | (loga(x))’= 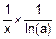
|
| e) | (ex)’=ex |
| f) | (ax)’=ax´ln(a) |
| g) | (sin(x))’=cos(x) |
| h) | (cos(x))’=-sin(x) |
(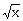 )’=
)’= 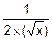 .
.
В табл. 5.1 сведены производные от некоторых из элементарных функций. Эту таблицу и перечисленные выше свойства 1..5 используют при вычислении производных любых функций.
 Пример. Доказать формулы d), e), f) в табл. 5.1, полагая, что остальные формулы доказаны:
Пример. Доказать формулы d), e), f) в табл. 5.1, полагая, что остальные формулы доказаны:
d) (loga(x))’= 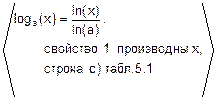 =
= 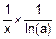 .
.
e) (ex)’= 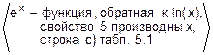 =
= 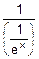 =ex.
=ex.
f) (ax)’= 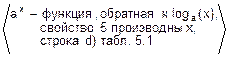 =ax´ln(a).
=ax´ln(a).
 Пример:
Пример:
(e-x)’= 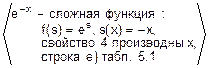 =-e-x.
=-e-x.
5.2. Свойства дифференцируемых функций
Производная – мощный инструмент для исследования функций. По результатам исследований устанавливаются следующие свойства дифференцируемых функций (без особенностей в области определения каждой из них).
Непрерывность. Если функция f(x) имеет производную в точке x=a, то она непрерывна в этой точке. Если функция имеет производную на интервале ]a,b[, то она непрерывна на этом интервале.
Монотонность. Если f’(x)>0 на интервале ]a,b[, то функция монотонно возрастает на этом интервале. Если f’(x)<0 на интервале ]d,e[, то функция монотонно убывает на этом интервале. Напомним, что функция возрастает (или убывает), если для любой пары x2>x1 имеет место f(x2)>f(x1) (или f(x2)<f(x1)).
Как мы уже знаем, f’(x) – тангенс угла наклона касательной к f(x) в точке x. Значит, угол наклона касательной в любой точке интервала возрастания функции 0<a< 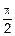 (участок AB кривой f(x) на рис.5.2), и
(участок AB кривой f(x) на рис.5.2), и 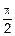 <b<p в любой точке интервала убывания функции (участок DE кривой f(x) на рис.5.2).
<b<p в любой точке интервала убывания функции (участок DE кривой f(x) на рис.5.2).
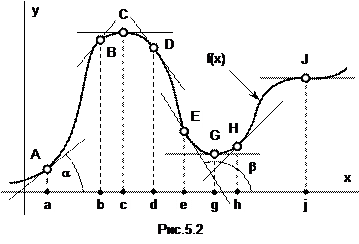
Максимумы и минимумы. Точка x=c называется точкой максимума функции f(x), если в некоторой окрестности точки c функция f(x) определена и f(x)£f(c) (точка C на кривой f(x) на рис.5.2). А точка x=g называется точкой минимума функции f(x), если в некоторой окрестности точки g функция f(x) определена и f(x)³f(g) (точка G на кривой f(x) на рис.5.2). Точки максимума и минимума функции называются точками ее экстремумов. В точке экстремума (рис.5.2) касательная к f(x) горизонтальна.
Если функция f(x) в точке x=xm достигает своего экстремума, то ее производная в этой точке равна нулю.
Это утверждение – суть теорема Ферма. Тот факт, что f’(xm)=0 – необходимое, но не достаточное условие экстремума функции в точке x=xm, а именно, обратное утверждение о том, что если в точке x=xj производная f’(xj)=0, то точка xj есть точка экстремума функции f(x), верно не всегда. Например, на рис.5.2 в точке J производная от f(j) равна нулю (касательная к f(x) в этой точке лежит горизонтально), но точка x=j не является точкой экстремума (слева от нее f(x)<f(j), а справа – f(x)>f(j)).
Сформулируем достаточное условие для существования экстремума функции в точке xm.
Пусть f’(xm)=0, а xl<xm и xr>xm. Тогда функция f(x) достигает своего экстремума в точке xm, если знаки величин f’(xl) и f’(xr) взаимно противоположны.
Какого именно экстремума достигает функция f(x) в точке xm, определяют так:
если f’(xl)>0, а f’(xr)<0, то xm – точка максимума функции f(x),
если f’(xl)<0, а f’(xl)>0, то xm – точка минимума функции f(x).
Итак, процедура отыскания экстремумов функции f(x) сводится к следующей последовательности действий:
§ вычисляют производную f‘(x) заданной функции f(x),
§ находят все корни x1, x2,¼, xm,¼, xn уравнения f’(x)=0,
§ для каждого из корней xm выполняют такие действия:
P отступают от xm влево, положив x=xl, и для этого значения x определяют знак производной f’(xl),
P отступают от xm вправо, положив x=xr, и для этого значения x определяют знак производной f’(xr),
P сравнивая знаки величин f’(xl) и f’(xr), определяют, какой именно экстремум функции f(x) отвечает точке xm.
Значения xl и xr выбирают удобными для вычисления значений f’(xl) и f’(xr).
 Пример. Найдем экстремумы функции
Пример. Найдем экстремумы функции
f(x)=2´x3-6´x2-18´x-15:
§ вычисляем f’(x)=6´x2-12´x-18.
§ решив уравнение 6´x2-12´x-18=0, найдем x0=-1, x1=3.
§ для x0 положим xl=-2, xr=0 и находим, что f’(-2)=30>0, а f’(0)=-18<0. Значит, точка x0=-1 есть точка максимума для f(x),
§ для x1 положим xl=0, xr=4 и находим, что f’(0)=-18<0, а f’(4)=30>0. Значит, точка x1=3 – точка минимума для f(x).
Заданная функция f(x) определена на всей числовой оси. Укажем на участки ее монотонности: при x<x0 функция возрастает, на интервале ]-1, 3[ – убывает, а при x> x1 снова возрастает.
Рассмотрим такую функцию: f(x)=(x-1)3. Ее производная f’(x)=3´(x-1)2 равна нулю в точке x1=1. Однако и слева от этой точки x<x1,и справа от нее x>x1 производная f’(x)>0. Значит, в этой точке экстремума функции f(x) нет.
5.3. Дифференциал функции
Дифференциалы переменных x, y и др. обозначают как dx, dy и т.д. Определяются дифференциалы по-разному, в зависимости от того, является ли величина независимой переменной (аргументом) или функцией.
Дифференциал аргумента – это любое его приращение:
dx=Dx.
Дифференциал функции y=f(x) есть произведение ее производной f’(x) на дифференциал независимой переменной dx:
dy=f’(x)´dx. (5.3)
Для дифференциала функции используют еще и такое обозначение:
d(f(x)).
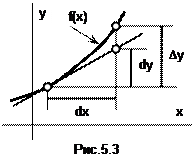
Рис.5.3 поясняет геометрический смысл дифференциала функции. Как видим, dy – это приращение, которое получает ордината касательной к f(x) в точке x при данном приращении аргумента dx. Говорят, что dy есть главная (линейная) часть приращения функции Dy. Это объясняется тем, что при малых dx приращение функции Dy почти совпадает с ее дифференциалом: Dy@dy (рис.5.3).
Из определения дифференциала функции (5.3) получают еще и такие обозначения для ее производной:
f’(x)= 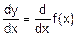 .
.
Правила вычисления производных задают и правила вычисления дифференциалов:
1. Если A,B=const, то d(A´f(x)+B´g(x))=A´df(x)+B´dg(x).
2. Дифференциал произведения функций:
d(f(x)´g(x))=df(x)´g(x)+ f(x)´dg(x).
3. Дифференциал отношения функций:
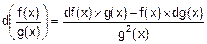 .
.
Понятие дифференциала широко используется в приближенных вычислениях. Так, для определения погрешности функции Dy, обусловленной погрешностью ее аргумента Dx, пользуются формулой:
Dy@dy=f’(x)´Dx. (5.4)
 Вычислим, к примеру, погрешность DS площади круга S, если его радиус r задается с точностью Dr.
Вычислим, к примеру, погрешность DS площади круга S, если его радиус r задается с точностью Dr.
S=p´r2, S+DS=p´(r+Dr)2, DS=2´p´r´Dr+p´Dr2.
А по формуле (5.4) получим:
DS@(p´r2)’´Dr=2´p´r´Dr.
Погрешность формулы (5.4) p´Dr2 при малых Dr близка к нулю.
Так как дифференциал dy – основная часть приращения функции Dy, при малых Dx имеет место приближенное равенство dy@Dy или же
f(x+Dx)-f(x)@f’(x)´Dx.
Отсюда
f(x+Dx)@f(x)+f’(x)´Dx. (5.5)
Полученная формула используется для приближенного вычисления нового значения функции f(x+Dx), когда заданы ее старое значение f(x) и величина Dx.
 Найдем, к примеру, значение
Найдем, к примеру, значение 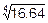 . Положим, что здесь f(x)=
. Положим, что здесь f(x)= 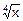 . Тогда f’(x)=
. Тогда f’(x)= 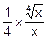 , x+Dx=16.64, x=16, а Dx=0.64. Значит, по формуле (5.5) получим:
, x+Dx=16.64, x=16, а Dx=0.64. Значит, по формуле (5.5) получим:
f(x+Dx)= 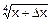 @
@ 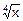 +
+ 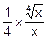 ´Dx=
´Dx= 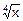 ´(1+
´(1+ 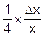 ).
).
|
|
|
|
|
Дата добавления: 2014-11-18; Просмотров: 355; Нарушение авторских прав?; Мы поможем в написании вашей работы!