Элементы статистической обработки данных 10 страница

P(F)=0.8, P(T)=0.5.

Каждая из гипотез – произведение двух событий из четырех: {F, ùF, T, ùT}:

H₀₀=ùF´ùT, H₁₀=F´ùT, H₀₁=ùF´T, H₁₁=F´T.

Их априорные вероятности таковы:

P(H₀₀)=P(ùF´ùT)=0.2´0.5=0.1; P(H₁₀)=P(F´ùT)=0.8´0.5=0.4;

P(H₀₁)=P(ùF´T)=0.2´0.5=0.1; P(H₁₁)=P(F´T)=0.8´0.5=0.4.

Очевидно, что

P(A½H₀₀)=0; P(A½H₁₀)=1;

P(A½H₀₁)=1; P(A½H₁₁)=0.

Справедливым будет делить добычу пропорционально апостериорным вероятностям гипотез H₁₀ и H₀₁,которые вычисляем по формуле Байеса:

P(H₁₀½A)= =

= = ;

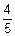P(H₀₁½A)= =

= = .

Итак, первому охотнику достанется 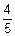, а второму – трофея.

Формула Бернулли. И снова начнем с примера. По мишени производится три независимых выстрела. Вероятность попадания в мишень при каждом выстреле равна p. Найти вероятность того, что при этих трех выстрелах получится ровно два попадания.

Обозначим через A₁, A₂, A₃ попадания при первом, при втором и при третьем выстрелах, а через ùA₁, ùA₂, ùA₃ – промахи при первом, при втором и при третьем выстрелах. При этом вероятность попадания при любом из выстрелов равна P(A_i)=p, а вероятность промаха при любом из выстрелов – P(ùA_i)=1-p=q, (i= ). Перечислим те исходы, в которых наблюдаются два попадания:

A₁´A₂´ùA₃ – попадания при первом и втором выстрелах, промах при третьем,

A₁´ùA₂´A₃ – попадания при первом и третьем выстрелах, промах при втором,

ùA₁´A₂´A₃ – промах при первом выстреле, попадания при втором и третьем.

Очевидно, что событие «ровно два попадания при трех выстрелах» - это сумма перечисленных исходов:

A₁´A₂´ùA₃+A₁´ùA₂´A₃+ùA₁´A₂´A₃.

Слагаемые в этой сумме – события несовместные, а сомножители в каждом из них – события независимые. Обозначим искомую вероятность события «ровно два попадания при трех выстрелах» как 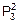и применим для ее вычисления формулы сложения и умножения вероятностей:

=P(A₁´A₂´ùA₃)+P(A₁´ùA₂´A₃)+P(ùA₁´A₂´A₃)=

=p´p´q+p´q´p+q´p´p=3´p²´q.

= ´p²´q.

Так мы получили формулу Бернулли для серии из n=3 испытаний, в которых событие A наступило ровно m=2 раза.

В общем случае формула Бернулли записывается так:

= ´p^m´q^n-m. (7.19)

Она позволяет вычислить вероятность того, что в n последовательных испытаниях успех будет достигнут ровно m раз.

Формула Бернулли применяется при решении таких задач. Пусть в результате случайного испытания некоторое событие A может наступить или не наступить. Наступление этого события в данном испытании называют успехом. Вероятность успеха равна p, вероятность неуспеха равна q=1-p. Испытание повторяют n раз. При этом соблюдаются следующие условия:

§ вероятность успеха P(A)=p в каждом испытании одна и та же,

§ результат любого испытания не зависит от результатов предыдущих испытаний.

Говорят, что такая последовательность испытаний с двумя исходами (успех/неудача) отвечает схеме Бернулли с параметрами p, q, n.

Из этой формулы Бернулли можно вывести такие простые следствия:

1. =pⁿ; =qⁿ; 2. + +¼+ + =1.

Пример. В урне 2 белых и 2 черных шара. Из нее наугад вынимают 2 шара и возвращают их обратно. Это испытание выполняют 4 раза. Найти вероятность того, что:

а) шары разного цвета вынуты ровно 3 раза,

б) шары разного цвета вынуты хотя бы один раз.

а) Очевидно, что здесь n=4, m=3 и нужно вычислить по формуле (7.19). Успех испытания A состоит в том, что из урны вынуты шары разного цвета, и для применения формулы (7.19) нужно найти P(A)=p и q=1-p.

При каждом испытании из урны берут 2 шара из 4. У такого испытания может быть m(W)= = =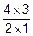6 исходов. Из них благоприятными для A будут исходы с шарами разного цвета. Такие исходы образуются так. Каждый из 2 белых шаров может сочетаться с любым из 2 черных, то есть действие «вынуть шары разного цвета» реализуется двумя способами – один белый с любым из двух черных. А всего таких действий два – два белых. Значит, по правилу умножения из комбинаторики (п. 7.1) m(A)=2´2=4. Отсюда по определению P(A)= = =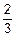p, а q=1-p= 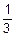. Теперь

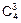= ´p³´q= 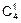´p³´q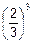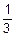=4´ ´ = @0.4.

б) Фраза «хотя бы один раз» означает, что имеет место событие B, состоящее или из одного успеха, или из двух, или из трех, или из четырех. Эти успехи несовместны, и потому

P(B)= + + + = + + + + - =

=1-q⁴=1- 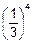= 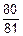@0.987.

Этот же результат можно получить и без использования следствия 2 из формулы Бернулли. Действительно, если событие B – «хотя бы один раз», то событие ùB – это «ни одного раза». Его вероятность P(ùB)= =q⁴. Значит, P(B)=1-q⁴.

Последний пример иллюстрирует принцип целесообразности применения в теории вероятностей противоположного события. Этот принцип можно сформулировать так.

Если противоположное событие распадается на меньшее число вариантов, чем прямое, то при вычислении вероятностей имеет смысл перейти к противоположному событию.

Вопросы и задачи для самоконтроля

1. Сформулировать правило умножения комбинаторики.

Сформулировать правило сложения комбинаторики.

2. Сформулировать понятие «перестановка» и записать формулу вычисления общего числа перестановок из n элементов.

Сформулировать понятие «размещение» и записать формулу вычисления общего числа размещений из n по k.

Сформулировать понятие «сочетание» и записать формулу вычисления общего числа сочетаний из n по k.

3. Анкета по изучению общественного мнения содержит 6 вопросов, на каждый из которых можно дать один из трех ответов: да, нет, не знаю. Найти общее число возможных вариантов заполнения анкеты. Сколько среди них анкет, которые содержат только разные ответы?

4. На занятии 10 студентов. Преподаватель может опросить любое число студентов, а может не опросить ни одного. Сколько существует вариантов для числа опрошенных студентов, если никто из них не опрашивается повторно, порядок опроса – произволен?

5. Сформулировать понятия «случайный эксперимент», «случайное событие», «элементарное событие», «пространство элементарных событий», «достоверное событие», «невозможное событие».

6. Двое играют в шахматы. Событие A – выиграл первый игрок, событие B – выиграл второй. Что означают записи:

а) ùB, б) ùA´ùB, в) ùA+ùB?

7. Дать классическое определение вероятности.

8. В урне 9 красных и 6 синих шаров. Наугад вынимают один. Какова вероятность вынуть красный шар?

9. Шифр замка сейфа набирают из цифр {1,2,3,4,5}. Длина кода – 4 разряда. Преступник пытается открыть сейф. Какова вероятность того, что он угадает шифр с первой попытки?

10. В учебной группе 25 студентов. Из них 5 студентов отличники, 10 – хорошисты. Из группы наугад выбирают одного студента на тестирование по математике. Какова вероятность того, что выбран отличник или хорошист?

11. Определить понятия событий независимых и зависимых, понятие условной вероятности.

Сформулировать теорему умножения вероятностей.

12. В юридическом колледже экзамен по математике сдают так. Каждый студент наугад выбирает 3 вопроса из 25. Положительная оценка выставляется при ответе на два или три вопроса. Студент Сухов выучил 15 вопросов. Вычислить вероятность того, что он:

а) получит пятерку,

б) получит положительную оценку,

в) не сдаст экзамен.

13. В течение месяца суд вынес 30 приговоров, в том числе 6 – по делам о краже. В порядке прокурорского надзора проверяется 10% дел. Какова вероятность того, что среди них окажется:

а) два дела о краже,

б) хотя бы одно дело о краже?

14. Записать формулу полной вероятности и пояснить, когда она применяется.

15. Записать формулу Байеса и пояснить, когда она применяется.

16. Из 10 лотерейных билетов 4 выигрышных.

а) Наугад один за другим без возвращения берут два билета. Какова вероятность того, что вторым будет выигрышный билет?

б) Вторым оказался выигрышный билет. Какова вероятность того, что первым был тоже выигрышный билет?

17. Пояснить, какой случайный эксперимент отвечает схеме Бернулли? Записать формулу Бернулли.

18. Каждый четвертый клиент банка приходит в банк брать проценты с вклада. Сейчас в банке ожидают своей очереди на обслуживание 6 клиентов. Найти вероятность того, что из них будут брать проценты а) только двое, б) хотя бы один.

19. Условия стрельбы таковы, что мишень поражается в 20% случаев. Сколько выстрелов нужно произвести, чтобы с вероятностью 0.9 попасть в мишень хотя бы один раз?

20. Выполнить ДКЗ: Тест 7. ПОНЯТИЕ ВЕРОЯТНОСТИ.

Глава 8. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ

8.1. Понятие случайной величины

Нередко результатом случайного эксперимента является числовая величина, значение которой в каждом эксперименте разное. Такая величина называется случайной. Например,

w число попаданий в мишень при трех выстрелах может принимать одно из следующих значений: 0, 1, 2, 3;

w показания ртутного медицинского термометра при измерении температуры пациента принимают одно из следующих значений: 34.1, 34.2,…,36.7,…,42.0.

В первом примере минимальное расстояние между соседними значениями (отсчетами) случайной величины равно единице, во втором – 0.1. Бывают случайные величины и с большими, и меньшими расстояниями между отсчетами.

Случайные величины СВ, у которых расстояние между соседними отсчетами – величина конечная, называются дискретными. Обычно набор значений у дискретных величин конечен (как в приведенных примерах).

В общем случае, дискретные случайные величины – числа рациональные. На числовой прямой они представлены точками, которые разделены конечными промежутками, а длина каждого из промежутков равна единице младшего разряда в записи этих чисел.

В случайных экспериментах действуют и со случайными величинами другой природы. Например,

w вес наугад взятого осколка бомбы,

w ошибка в измерении скорости движения автомобиля.

Возможные значения каждой из таких величин одно от другого не отделены, и образуют на числовой прямой сплошной массив точек. А это вещественные числа.

Случайные величины, у которых значения – суть вещественные числа, называются непрерывными. В общем случае, возможный набор значений непрерывной случайной величины – вся числовая прямая. Работают и с такими непрерывными случайными величинами, значения которых – интервал на числовой прямой.

Если классическая теория вероятностей имеет дело по преимуществу с событиями нечисловой природы, то современная теория вероятностей оперирует с числами – случайными величинами. Это стремятся делать даже и тогда, когда результатом случайного эксперимента число не является.

Например, проводится опыт, в результате которого может наступить или не наступить событие A. Событию A можно сопоставить число X, которое принимает значение 1 при наступлении A, и оно равно 0, когда A не наступило. Теперь X – дискретная случайная величина, которая характеризует событие A. Возможные ее значения – {0,1}.

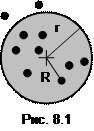Еще пример. Событие B – попадание при стрельбе в круглую мишень (рис. 8.1). Обозначим радиус круга как r, а расстояние от центра мишени до точки попадания пули как R. Тогда наступлению события B отвечает выполнение неравенства R<r, то есть вероятность события B – не что иное, как вероятность того, что это неравенство выполняются.

Итак, в современной теории вероятностей, где только возможно, от схемы случайных событий переходят к схеме случайных величин. Эта схема предоставляет для решения задач, относящихся к случайным явлениям, более гибкий и универсальный аппарат высшей математики.

8.2. Законы распределения случайных величин

Всякое соотношение, которое устанавливает связь между возможными значениями случайной величины и вероятностями этих значений, называют законом распределения этой СВ.

Изучение законов распределения начнем с дискретных случайных величин.

Ряд распределения. Обозначим дискретную СВ как X, а набор ее отсчетов – как x₀, x₁,…, x_n. Исход случайного эксперимента – событие X=x_k характеризуется вероятностью P(X=x_k)=p_k. Факт равенства чисел X=x_k устанавливают путем последовательного сравнения цифр в одноименных разрядах записей X и x_k (см. рис. 8.2). Если имеет место a_i=b_i для всех i=r,r-1,¼,-m, то числа X и x_k равны.

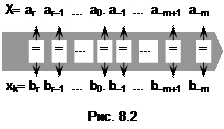
Сопоставим каждому отсчету x_k случайной величины X вероятность p_k. В результате получим закон распределения дискретной СВ X. Самой простой формой записи закона распределения дискретной случайной величины является таблица, в первой строке которой перечисляются ее отсчеты x_k, а во второй – вероятности p_k. Такую таблицу {x_k,p_k} и называют рядом распределения.

Очевидно, что события X=x_k, k= образуют полную группу, и поэтому .

Пример. Стрелок производит три выстрела по мишени. Вероятность попадания в мишень при каждом выстреле равна 0.6. Построить ряд распределения для числа попаданий в мишень при трех выстрелах.

Обозначим как Z дискретную случайную величину – число попаданий в мишень. Набор ее значений: z₀=0, z₁=1, z₂=2, z₃=3. Опыт укладывается в схему Бернулли. Поэтому вероятность события Z=z_k вычисляем по формуле Бернулли:

p₀= =0.4³=0.064,

p₁= = ´0.6´0,4²=0.288,

p₂= 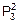= ´0.6²´0.4=0.432,

p₃= =0.6³=0.216.

Теперь составляем табл.8.1 – ряд распределения случайной величины Z.

Таблица 8.1
zk
pk	0.064	0.288	0.432	0.216

Закон распределения для непрерывных СВ задается функцией распределения и/или плотностью распределения.

Функция распределения. Напомним, что непрерывная СВ X – число вещественное. Точно так и возможное ее значение величина x – точка в сплошном массиве точек на числовой оси тоже число вещественное. В записи каждого вещественного числа дробная часть имеет бесконечную длину. Поэтому для вещественных чисел нельзя установить факт их равенства в силу того, что процедуру последовательного сравнения цифр в одноименных разрядах записей завершить невозможно. Зато путем последовательного сравнения цифр в одноименных разрядах этих записей можно установить факт a_j¹b_j, j=r, r-1,…(см. рис. 8.3), а, значит, и факт X¹x. На этом процедура последовательного сравнения цифр в одноименных разрядах записей X и x завершается.

При построении закона распределения непрерывной случайной величины X оперируют с событием X<x. Это неравенство можно зафиксировать путем последовательного сравнения цифр в одноименных разрядах записей X и x. Напомним, что здесь X – результат случайного эксперимента, а x – любая точка на числовой прямой, то есть x является независимой переменной. Значит, вероятность события X<x есть некоторая функция переменной x. Ее и называют функцией распределения случайной величины X и обозначают как F(x):

F(x)=P(X<x). (8.1)

Прежде чем двигаться дальше, отметим глубокий философский смысл этого определения. В левой части (8.1) записана функция действительного аргумента, а в правой – вероятность некоторого события. Функция является одним из фундаментальных понятий математического анализа, той области математики, где изучаются жестко определенные закономерности. Вероятность – фундаментальное понятие теории вероятностей, которая изучает закономерности в мире случайного. Формула (8.1) перебрасывает мост между математическим анализом и теорией вероятностей. Тем самым строгий, хорошо разработанный аппарат математического анализа становится мощным инструментом исследования случайных величин в теории вероятностей.

Перечислим общие свойства функции распределения.

1. Функция F(x) – неубывающая функция своего аргумента, то есть при x₂>x₁ и F(x₂)³F(x₁).

2. F(+¥)=1.

3. F(-¥)=0.

К этим свойствам приведем геометрические пояснения (рис. 8.4). Пусть x – точка на оси 0x. Случайная величина X в результате опыта может занять на этой же оси то или иное положение. Тогда F(x)=P(X<x) – вероятность того, что X попадет в зону на оси левее точки x (в заштрихованную зону). При увеличении x заштрихованная область левее него увеличивается. Поэтому вероятность P(X<x) уменьшиться не может. Следовательно, F(x) с ростом x не убывает (свойство 1).

Очевидно, что при x®+¥ заштрихованная область левее x становится бесконечно большой, и попадание в нее X оказывается событием достоверным. Поэтому F(+¥)=P(X<+¥)=1 (свойство 2). Точно так, при x®-¥ попадание X левее x становится невозможным, и F(-¥)=P(X<-¥)=0 (свойство 3).

Пример. Функция распределения непрерывной случайной величины W задана формулой:

F(w)= 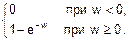(8.2)

График этой функции показан на рис. 8.5,а. Как видим, F(x) обладает всеми указанными свойствами.

Плотность распределения. Для непрерывной случайной величины X функция распределения F(x) непрерывна, а значит, и дифференцируема на всей числовой оси. Продифференцировав F(x), получим функцию

f(x)=F’(x), (8.3)

которая называется плотностью распределения или плотностью вероятности (по аналогии с плотностью вещества).

Пример. Плотность распределения f(w) случайной величины, у которой F(w) задана формулой (8.2):

f(w)= (8.4)

На рис. 8.5,б показан график плотности распределения (8.4). Его называют кривой распределения непрерывной СВ.

Рассмотрим свойства плотности распределения.

1. Плотность распределения – функция неотрицательная:

f(x)³0 для -¥<x<+¥.

2. Полная площадь под кривой распределения равна единице:

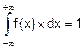
(событие -¥<X<+¥ достоверно, его вероятность равна единице).

Отметим важное обстоятельство. Случайная величина X обычно имеет размерность. Отсчеты функции F(x) размерности не имеют. А вот отсчеты f(x) имеют размерность, обратную размерности случайной величины X.

Когда задана функция распределения F(x) плотность вероятности f(x) вычисляют по формуле (8.3). А если задана плотность распределения f(x), то функцию распределения F(x) вычисляют так:

F(x)= 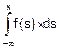. (8.5)

Поэтому функцию F(x) называют интегральным законом распределения, а функцию f(x) называют дифференциальным законом распределения непрерывной СВ.

Вероятность попадания случайной величины в заданный диапазон. Зададим на оси 0x две точки a, b и вычислим вероятность такого события a£X<b, а именно, вероятность того, что случайная величина X в результате опыта попадет в диапазон, ограниченный точками a и b. Для этого рассмотрим такие события (рис. 8.6):

A: X<b, B: X<a, C: a£X<b.

События B и C несовместны, так как X не может оказаться одновременно и слева, и справа от точки a. Событие A – сумма событий B и C: A=B+C (рис. 8.6). По формуле сложения вероятностей для несовместных случайных событий имеем:

P(X<b)=P(X<a)+P(a£X<b)

или с учетом определения (8.1)

F(b)=F(a)+P(a£X<b).

Откуда следует, что

P(a£X<b)=F(b)-F(a).

Таким образом, вероятность попадания случайной величины в заданный диапазон равна приращению ее функции распределения на этом диапазоне.

Укажем на любопытное следствие из последней формулы. Пусть X – непрерывная случайная величина. Будем неограниченно уменьшать размер диапазона путем b®a. В результате получим событие X=a, вероятность которого есть

P(x=a)= = =0.

Как видим, вероятность отдельного точечного значения непрерывной случайной величины равна нулю! Другими словами, для непрерывной случайной величины вероятность события X=a равна нулю, но событие это возможно (результат случайного эксперимента X может попасть в точку a на числовой прямой). Поскольку P(X=a)=0, неравенства a£X<b эквивалентны неравенствам a<X<b. Эти строгие неравенства и используют при вычислении вероятности попадания случайной величины в заданный диапазон (в интервал ]a,b[)

P(a<X<b)=F(b)-F(a). (8.6)

Пример. Вычислить вероятность попадания СВ W, для которой функция распределения F(x) определена формулой (8.2), в диапазон от a=1 до b=3.

Когда задана F(x) (см. рис. 8.5,а), действуем по формуле (8.6),:

P(1<W<3)=F(3)-F(1)=0.95-0.63=0.32.

Приращение функции распределения на интервале ]1,3[, а именно, число F(3)-F(1)=P(1<W<3)=0.32 показано на рис. 8.5,а.

Если же задана плотность распределения f(x), вероятность события a<X<b вычисляется так:

P(a<X<b)= . (8.7)

Таким образом, вероятность попадания случайной величины в заданный диапазон равна площади под кривой f(x) на интервале ]a,b[.

Пример. Плотность вероятности f(x) случайной величины W задана формулой (8.4). Вычислить вероятность попадания W в диапазон от a=1 b=3. Действуем по формуле (8.7):

P(1<X<3)= 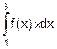=F(3)-F(1)=0.32.

Теперьчисло P(1<X<3)=0.32 – заштрихованная площадь под кривой f(x) на интервале ]1,3[ (см. рис. 8.5,б).

8.3. Числовые характеристики случайных величин

Закон распределения той или иной случайной величины описывает ее с вероятностной точки зрения в полной мере. Любые задачи, связанные со случайными величинами, могут быть решены с помощью законов распределения. Однако далеко не все задачи подобного рода требуют для их решения такой тяжелой артиллерии. Бывает достаточно оперировать с компактными характеристиками, отражающими самые существенные особенности случайных величин. Для этих целей и служат числовые характеристики случайных величин. В первую очередь, это математическое ожидание и дисперсия случайной величины.

Математическое ожидание МО характеризует местоположение случайной величины на числовой оси. Это своего рода центр тяжести всего массива ее отсчетов. Обозначают математическое ожидание случайной величины X как M[X], либо как m_x. Математическое ожидание случайной величины X называют еще и ее средним.

Дата добавления: 2014-11-18