Замечательные пределы

I Первый замечательный предел

Теорема 1. .

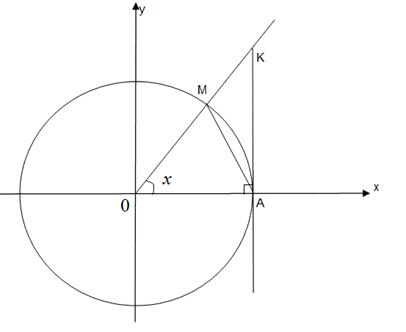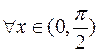Доказательство. Сначала докажем основное неравенство , справедливое . Для этого рассмотрим единичную окружность с центром в начале координат и пусть - точка окружности, лежащая в первой четверти. Через проведем луч 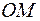, а через точку - касательную к окружности. Если радианная мера равна , то и 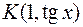. Рассмотрим три фигуры: 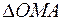, сектор 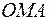и 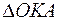. Очевидно, 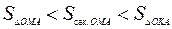, что означает следующее: . Отсюда и получаем основное неравенство.

Далее докажем три леммы.

Лемма 1. .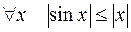

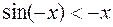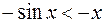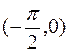
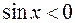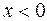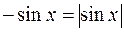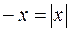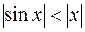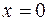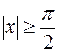Для - это часть основного неравенства. Если , то и поэтому или . Но в интервале и , следовательно, , и снова . Если , то . Пусть, наконец, . Тогд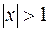а , а 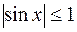. И снова .

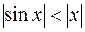Лемма 2. .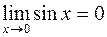

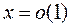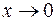Это следствие одного из свойств б.м. функций: если при и 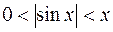, то 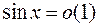и при 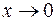, т.е. .

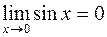Лемма 3. .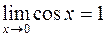

Преобразуем: .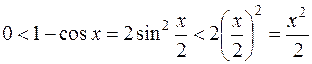

И снова, т.к. 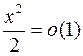при 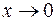, то и при 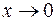. Это же означает: .

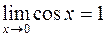Теперь можем доказать теорему. Пусть 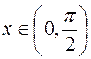. Разделим все части основного неравенства на : .

Переходя к обратным величинам, получим:

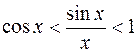. (1)

Применяя к полученному неравенству теорему 9 из предыдущего параграфа и учитывая, что , получим

.

Пусть теперь 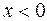, тогда и неравенство (1) принимает вид

.

Принимая во внимание четность и нечетность 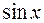, и для 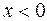получаем неравенство (1), а значит и

.

Равенство односторонних пределов и доказывает теорему.

Если объединить доказанную теорему с теоремой 10 из § 9, то можно получить более сильный результат.

Теорема 2. Пусть 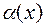- произвольная б.м. функция при . Тогда

.

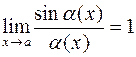Примеры.

1.

.

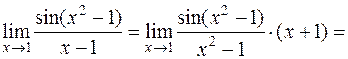
2. .

Сделаем замену 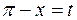. Тогда и при 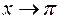. Поэтому

.

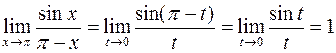3. .

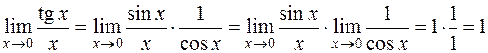II Второй замечательный предел

В § 8 было доказано, что предел последовательности равен числу . Оказывается, этот результат справедлив и для функции при 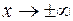(доказательство опустим). Переходя от бесконечно больших к бесконечно малым получим т.н. второй замечательный предел.

Теорема 3. .

Более того, для любо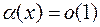й при имеет место равенство

.

Примеры.

4.

.

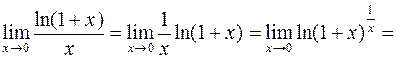
Здесь знак предела был внесен под знак 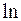в связи с тем, что функция 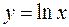- непрерывная (смотри об этом в последующих параграфах).

5. .

Лекция 6

Дата добавления: 2014-11-08