Устойчивость систем с запаздыванием и систем с иррациональными звеньями

Системы автоматического управления могут содержать звенья, и которых зависимость между входной u(t)и выход­ной у(t)величинами имеет вид

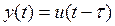(3.145)

где 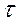— постоянная величина, называемая временем запазды­вания. Такие звенья называют запаздывающими, так как они воспроизводят изменения входной величины без искажения, но с некоторым постоянным запаздыванием .

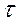Передаточная функция запаздывающего звена:

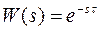(3.146)

Звенья с чистым запаздыванием часто встречаются в различ­ных технологических процессах. Например, материал перемещает­ся из одной точки в другую с помощью ленточных транспор­теров; в системах регулирования толщины листа при прокат­ке; в системах магнитной записи и воспроизведения и т. д. Системы автоматического управления, содержащие хотя быодно запаздывающее звено, называют системами сзапазды­ванием. Процессы в системах с запаздыванием описываются дифференциально-разностными уравнениями.

Во многих тепловых процессах, а также при передаче сигналов на расстояние по длинным электрическим, гидравлическим и другим линиям наблюдается запаздывание, распределенное по всей длине ли­нии, которое в отличие от чистого запаздывания приводит к искажению передаваемых сигналов. Системы, содержащие звенья с распределен­ным запаздыванием, требуют для своего описания дифференциальных уравнений в частных производных. Во многих случаях в результате решения указанных уравнений в частных производных с учетом гра­ничных условий после некоторых упрощающих предположений для си­стемы автоматического управления в целом получают дифференциаль­но-разностные уравнения такого же типа, как и для систем с чистым запаздыванием.

На практике широко применяют аппроксимацию передаточных функций сложных систем с распределением параметрами с помощью передаточных функций систем с сосредоточенными параметрами и эк­вивалентных постоянных времени чистого запаздывания. Иногда слож­ные системы высокого порядка с сосредоточенными параметрами, со­держащие большое количество инерционных звеньев, также мож­но заменить для приближенного исследования более простой системой низкого порядка, но содержащей звенья с чистым запаздыванием. В дальнейшем будем рассматривать только системы с чистым за­паздыванием.

Структурная схема одноконтурной системы автоматическо­го управления, содержащей одно запаздывающее звено, может быть представлена либо так, как показано на рис. 3.32 а, а,если запаздывающее звено находится в прямой цепи, либо так, как показано на рис. 3.32 б, если запаздывающее звено нахо­дится в цепи обратной связи.

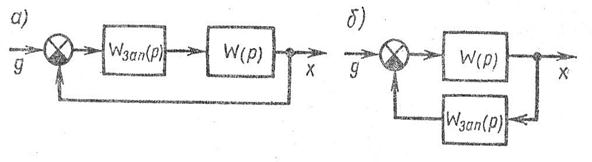
Рис.3.32. Структурная схема САУ с звеном запаздывания

Передаточная функция разомкнутой системы с запаздыва­нием равна

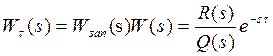(3.147)

где W(s) — R(s)/Q(s)— передаточная функция разомкнутой системы без учета запаздывания, представляющая собой дроб­но-рациональную функцию оператора s.

Заметим, что если в одноконтурной системе имеется не­сколько последовательно соединенных запаздывающих звень­ев, то они могут быть заменены одним запаздывающим звеном с эквивалентной постоянной времени запаздывания, равной сумме всех постоянных времен запаздывания.

Если запаздывающее звено находится в прямой цепи, то передаточная функция замкнутой системы

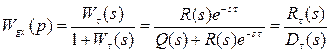(3.148)

Если же запаздывающее звено находится в цепи обратной связи, то передаточная функция замкнутой системы

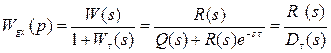(3.149)

Из (4) и (5) видно, что независимо от места включе­ния запаздывающего звена характеристическое уравнение сис­темы с запаздыванием имеет вид

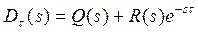(3.150)

Это характеристическое уравнение из-за наличия множите­ля 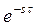является не полиномом, а трансцендентной функцией оператора s и в отличие от обыкновенного алгебраического уравнения имеет бесконечное множество корней. Так как

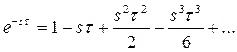(3.151)

то (6) можно рассматривать как уравнение «бесконечной степени».

Для того чтобы линейная система с постоянным запазды­ванием была устойчива, необходимо и достаточно, чтобы все корни уравнения (6) были левыми. Нахождение корней уравнения (6) затруднительно, поэтому для исследования устойчивости систем с запаздыванием используют критерии устойчивости.

Следует иметь в виду, что алгебраические критерии устой­чивостиРауса иГурвица в их обычной форме для исследования систем с запаздываниемнепригодны,причем для устойчивости линейных систем первого и второго порядков с запаздыванием только положительности коэффициентов характеристическо­го уравнения уже становится недостаточно. Существуют раз­личные алгебраические критерии устойчивости для систем с запаздыванием, которые являются аналогами крите­риев Рауса и Гурвица, однако в инженерной практике они широкого применения не нашли из-за их относительной слож­ности.

Для исследования устойчивости систем с запаздыванием можно применять основанные на принципе аргумента частот­ные критерии устойчивости Михайлова и Найквиста либо ме­тод D-разбиения.

Уравнение кривой (годографа) Михайлова системы с запаз­дыванием получают после подстановки s = jω в характеристи­ческое уравнение (6), т. е.

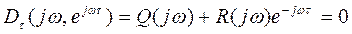(3.152)

Наличие в (7) множителя 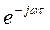делает очертания кри­вой Михайлова достаточно сложными, и формулировка этого критерия для систем с запаздыванием, становится не такой про­стой, как для обычных систем. Для исследования устойчивости систем с запаздыванием очень удобно применять критерий устойчивости Найквиста.

Заключение об устойчивости замкнутой системы с запазды­ванием делается на основании исследования поведения ампли­тудно-фазовой характеристики 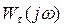разомкнутой системы с запаздыванием относительно точки (—1, j0). Формулировка критерия устойчивости Найквиста для систем с запаздыва­нием в этом случае аналогична формулировке для обычных систем, имеющих дробно-рациональные передаточные функции.

Частотную передаточную функцию 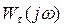разомкнутой системы с запаздыванием находят, подставляя s = jω в (3):

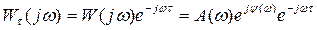(3.153)

где W(jω) = U(ω) + jV(ω) — амплитудно-фазовая харак­теристика разомкнутой системы без учета запаздывания;

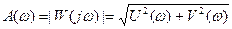—амплитудно-частотная характеристика;

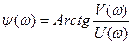- фазочастотная ха­рактеристика разомкнутой системы без учета запаздывания;

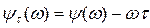(3.154)

— фазочастотная характеристика разомкнутой системы с за­паздыванием.

Из (8) и (9) видно, что наличие запаздывающего зве­на не меняет модуля А(ω) амплитудно-фазовой характери­стики разомкнутой системы 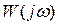, а вносит лишь дополни­тельный отрицательный фазовый сдвиг 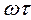, пропорциональный частоте, причем коэффициентом пропорциональности являет­ся время запаздывания .

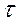Зная амплитудно-фазовую характеристику 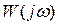разом­кнутой системы без запаздывания, легко построить амплитуд­но-фазовую характеристику 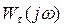разомкнутой системы с за­паздыванием. Для этого каждый модуль А(ω_i) вектора ам­плитудно-фазовой характеристики 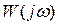нужно повернуть на угол 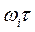по часовой стрелке. С ростом частоты ω угол 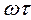будет быстро расти, а модуль А(ω) обычно уменьшается, по­этому амплитудно-фазовая характеристика 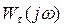разомкну­той системы с запаздыванием имеет вид спирали, закручиваю­щейся вокруг начала координат (рис. 3.33).

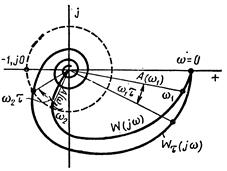
Рис. 3.33. АФЧХ разомкну­той системы с запаздыванием

«Закручивание» амплитудно-фазовой характеристики из-за наличия дополни­тельного фазового сдвига ωτ, вообще говоря, ухудшает усло­вие устойчивости, так как вся амплитудно-фазовая характе­ристика приближается к критической точке (—1, j0). Однако иногда при сложной форме амплитудно-фазовой характери­стики 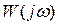введение постоянного запаздывания может улуч­шить условия устойчивости.

Изменяя время запаздыва­ния τ в широких пределах, можно найти такое его зна­чение, при котором замкну­тая система будет находить­ся на границе устойчивости. В этом случае характери­стика 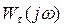будет прохо­дить через точку (—1, j0). Время запаздывания 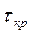и соответствующее ему значе­ние частоты ω_кр, при которых 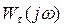проходит через точку (—1,j0), называют крити­ческими.

Для критического случая справедливо следующее условие:

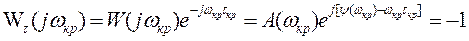(3.155)

Условие (10) можно записать раздельно для амплитуд и фаз вектора, :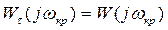

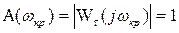; (3.156)

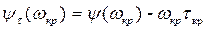, (3.157)

где i = 0, 1, 2, 3,...

Из (11) можно найти сначала ω_кр, а затем из (12) найти τ _кр, т. е.

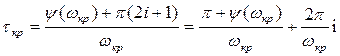(3.158)

Для систем автоматического управления с запаздыванием основное значение имеет минимальное критическое время за­паздывания(при i = 0), которое является в то же время и граничным

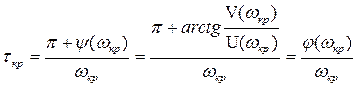, (3.159)

где 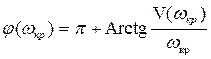- запас устойчивости по фазе

При сложном выражении для частотной передаточной функ­ции W(jω) разомкнутой системы определение критического времени запаздывания просто выполнить графически. Условие 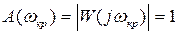определяется пересечением годо­графа W(jω) с окружностью единичного радиуса с центром в начале координат (рис. 3.34). Точка пересечения определяет одновременно 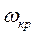и угол 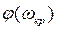, который, будучи разделен на 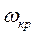, даст значение критического времени запаздывания.

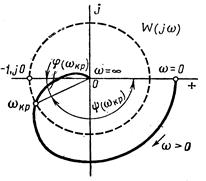
Рис. 3.34. Определение критического времени запаздывания.

Если имеется несколько точек пересечения годографа W(jω) с окружностью единичного радиуса, например при 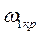, , 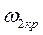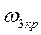(рис. 3.35), то система будет иметь несколь­ко критических граничных времен запаздывания:

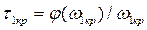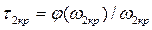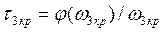; ; . (3.160)

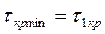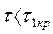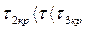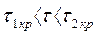причем минимальное время запаздывания равно . Система будет устойчива при , а также при . Система будет неустойчива при , а также при 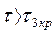. Наблюдаемое в этом случае чередование участков устойчивости и неустойчивости системы при непрерывном изменении 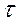(а также других параметров си­стемы) является характерной особенностью многих систем с постоянным запаздыванием.

Обычно для повышения быстродействия и точности систе­мы время запаздывания 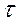стремятся уменьшить, поэтому кри­терий устойчивости формулируется лишь для минимального времени запаздывания.

Система автоматического управления будет устойчива, если время запаздывания 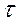меньше минимального критическо­го времени запаздывания: .

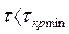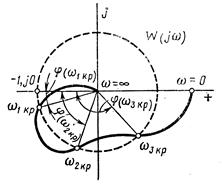
Рис. 3.35. Определение нескольких критических времен запаздывания

Критическое время запаздывания легко определяют и в том случае, когда для исследования системы с запаздыванием применяют логарифмические амплитудно-частотные (ЛАХ) и фазочастотные (ЛФХ) характеристики. В этом случае окруж­ность единичного радиуса представляют осью абцисс. ЛАХ системы с запаздыванием совпадает с ЛАХ исходной системы без запаздывания. Дополнительный фазовый сдвиг, который надо учесть при построении ЛФХ системы с запаздыванием, определяют из (9). Точки пересечения ЛАХ с осью абсцисс определяют критические частоты 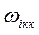, а запасы по фазе (с учетом кратности), отнесенные к соответствующим критиче­ским частотам, определяют критические времена запаздывания

Звенья с распределенными параметрами, описываемые уравнениями в частных производных, имеют иногда передаточ­ные функции вида

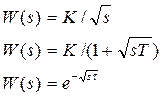, (3.161)

где К— коэффициент усиления звена.

Первые два выражения из (3.160) отличаются от передаточных функций интегрирующего и инерционного звеньев только квадратным корнем. По аналогии с интегрирующими и инерционными звеньями такие звенья называют полуинте­грирующими и полуинерционными. Звенья, имеющие переда­точные функции вида (3.160), называют ир­рациональными звеньями. Последнее выражение из (3.160) не только ирра­ционально, но и трансцендентно. С иррациональными звенья­ми приходится встречаться, рассматривая различные диффузионные и тепловые объекты, линии связи с потерями, с рас­пределенными сопротивлениями и емкостями и т. п.

Устойчивость замкнутых систем автоматического управле­ния, содержащих иррациональные звенья, может быть иссле­дована с помощью критерия устойчивости Найквиста. Форму­лировка критерия устойчивости Найквиста в этом случае ана­логична формулировке для обычных систем автоматического управления, содержащих звенья с дробно-рациональными пере­даточными функциями.

Пример 1. Пусть задана передаточная функция разомкнутой системы с за­паздыванием

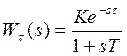(3.162)

Необходимо определить критическое время запаздывания .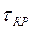

Частотная передаточная функция разомкнутой системы с запазды­ванием

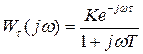(3.163)

Следовательно, условие () в данном случае

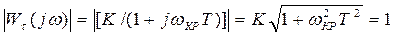(3.164)

Из последнего выражения находим критическую частоту:

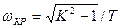, K > 1 (3.165)

Фазовый сдвиг на критической частоте

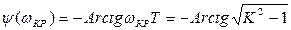(3.166)

По (3.105) находим критическое время запаздывания:

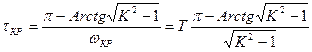(3.167)

Пример 2. Исследовать на устойчивость систему автоматического регулирования (рис. 3.36) с помощью критерия Найквиста.

Исходными данными являются передаточные функции объекта и регулятора:

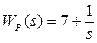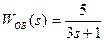; . (3.168)

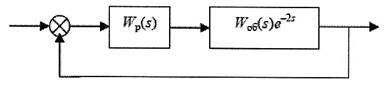
Pис. 3.36 Структурная схема САР с запаздыванием

Критерий устойчивости Найквиста, в отличие от предыдущих критериев, применяется для исследования устойчивости систем автоматического управления с запаздыванием, поэтому в данной задаче рассматривается объект с запаздыванием. Критерий Найквиста дает ответ об устойчивости замкнутой системы по АФХ разомкнутой системы. Он имеет три формулировки в зависимости от того устойчива, нейтральна или неустойчива разомкнутая система. Поэтому, прежде всего, необходимо ответить на вопрос об устойчивости разомкнутой системы.

Исследуем на устойчивость разомкнутую систему известными методами. Для записи передаточной функции разомкнутой системы разорвем обратную связь в замкнутой системе. Разомкнутая система представляет собой последовательно соединенные объект и регулятор, ее передаточная функция запишется в виде

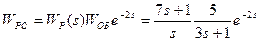(3.169)

Характеристическое уравнение разомкнутой системы - это знаменатель передаточной функции, приравненный к нулю:

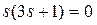(3.170)

Корни характеристического уравнения s₁ = s₂ = - 1/3. В соответствии с необходимым и достаточным условием устойчивости разомкнутая система будет нейтральной. Критерий Найквиста в этом случае звучит если разомкнутая система нейтральна, то для того чтобы замкнутая система была устойчивой, необходимо и достаточно, чтобы АФХ разомкнутой системы с добавлением в бесконечность не охватывала точку (-1, j0).

Для ответа на вопрос об устойчивости замкнутой системы по критерию Найквиста про­ще всего построить АФХ разомкнутой системы и посмотреть охватывает она точку (-1, j0) или нет, поэтому запишем выражение для АФХ разомкнутой системы:

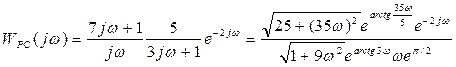(3.171)

откуда АЧХ:

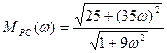(3.172)

и ФЧХ:

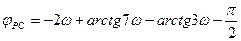(3.173)

Задаваясь значениями частот построим годограф АФХ разомкнутой системы (рис. 3.37). Как видно из рисунка АФХ разомкнутой системы охватывает точку (-1, j0), что говорит о том, что замкнутая система неустойчива.

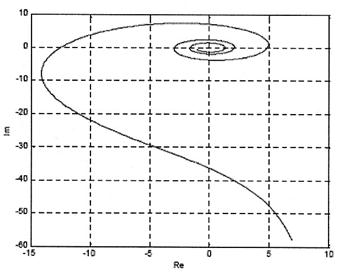
Рис. 3.37. Годограф АФХ разомкнутой системы

Дата добавления: 2014-11-20