Общая постановка задачи устойчивости по А.М. Ляпунову

Впервые строгое определение устойчивости было дано рус­ским ученым А. М. Ляпуновым в 1892 г. Отсутствие такого определения часто приводило к недоразумениям, так как движение, устойчи­вое в одном смысле, может оказаться неустойчивым при другом понимании этих слов, и наоборот. Определение устойчиво­сти А. М. Ляпунова оказалось настолько удачным и наилуч­шим образом удовлетворяющим многим техническим задачам, что оно в настоящее время принято как основное.

Пусть движение системы автоматического управления опи­сывается дифференциальными уравнениями, которые могут быть приведены к виду

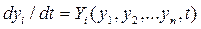, (3.2)

где у_i -- вещественные переменные, характеризующие состоя­ние системы управления (обобщенные координаты); Y_i — из­вестные функции переменных y_l у₂,..., у_nи времени t,удовлетворяющие условиям существования и единственности реше­ния.

Исходное состояние системы при 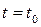однозначно опре­деляется начальными значениями переменных 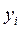, которые обозначим .

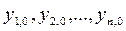Каждой совокупности начальных значений 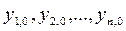соответствует единственное решение (3.2) для всех 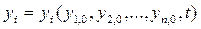(3.3)

Решение (3.3) описывает какое-либо движение системы, оп­ределяемое исходным состоянием.

Некоторое вполне определенное движение системы, подле­жащее исследованию на устойчивость, называют невозмущен­ным движением.

Заметим, что выбор невозмущенного движения является произвольным. Это может быть любое возможное движение системы, как установившееся, так и неустановившееся. До­пустим, что в качестве невозмущенного движения выбрано та­кое, которое описывается заданными функциями времени

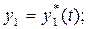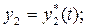
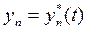; (3.4)

Предположим, что функции 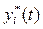являются частным ре­шением дифференциальных уравнений (3.2), т. е.

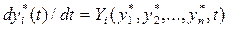(3.5)

удовлетворяющим начальным условиям при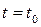

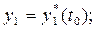
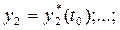
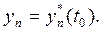(3.6)

В частном случае, когда параметры системы не изменяют­ся со временем и функции Y,не зависят явно от t,движения (3.4) являются установившимися. Им отвечают решения

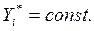, (3.7)

служащие корнями уравнений

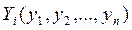. (3.8)

Изменим условия (3.6), дав начальным значениям 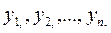перемен­ных небольшие по модулю приращения 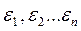т. е. пусть при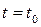

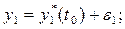
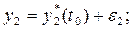
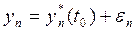(3.9)

Движение системы, отвечающее измененным начальным усло­виям (3.9), называют возмущенным движением.Другими словами, возмущенным движением системы называют всякое иноедвижение системы, отличное от невозмущенного.

Введем новые переменные:

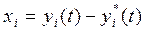(3.10)

равные разности переменных 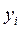в возмущенном и невозмущен­ном движении. Переменные 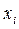называют отклонениямиили вариациямивеличин 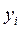.Если все отклонения равны нулю

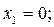
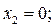
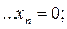(3.11)

то возмущенное движение 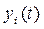будет совпадать с невозмущен­ным движением 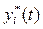,т. е. невозмущенному движению отве­чают нулевые значения переменных .

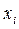Пусть при 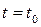переменные 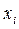принимают какие-либо на­чальные значения 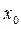, из которых по крайней мере одно не равно нулю:

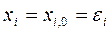(3.12)

Начальные значения отклонений (3.12) называют возмуще­ниями.

А. М. Ляпуновым было дано следующее определение устой­чивости: невозмущенное движение называют устойчивым по от­ношению к переменным 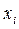если при всяком произвольно задан­ном положительном числе ε, как бы мало оно ни было, можно выбрать другое такое положительное число δ(ε), что при вся­ких возмущениях x_i0, удовлетворяющих условию

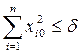(3.13)

и при любом t ≥ t₀ будет выполняться неравенство

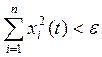(3.14)

в противном случае движение неустойчиво.

Геометрическая интерпретация этого условия заключается в следующем. В пространстве координат x_i построим две сферы с радиусами δ и ε (ε > δ). Система будет устойчивой, если при возмущениях, не выведших изображающую точку 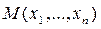из пределов сферы δ, возмущенное движение будет таково, что, начиная с некоторого времени t ≥ T, изображающая точка 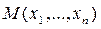будет в пределах сферы ε.

Практически устойчивость данного невозмущенного дви­жения означает, что при достаточно малых начальных возму­щениях возмущенное движение будет сколь угодно мало от­личаться от невозмущенного движения. Если невозмущенное движение неустойчиво, то возмущенное движение будет отхо­дить от него, как бы малы ни были начальные возмущения.

Если невозмущенное движение устойчиво и при этом любое возмущенное движение при достаточно малых начальных воз­мущениях стремится к невозмущенному движению, т. е.

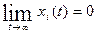, (3.15)

то невозмущенное движение называют асимптотически устой­чивым.

При асимптотической устойчивости изображающая точка с течением времени должна неограниченно стремиться к нача­лу координат.

Отметим некоторые особенности определения устойчивости по А. М.Ляпунову.

Во-первых, предполагают, что возмуще­ния налагаются только на начальные условия, иначе говоря, возмущенное движение происходит при тех же силах (источниках энер­гии), что и невозмущенное движение.

Во-вторых, устойчивость рассматрива­ют на бесконечно большом промежут­ке времени.

В-третьих, возмущения предполагаются малыми.

Несмотря на эти ограничения, определение А. М. Ляпунова устойчивости движения является эффективным в приложениях.

Дата добавления: 2014-11-20