Проблема самоприменимости

Кодирование и нумерация машин Тьюринга.

Зафиксируем счетные множества символов {a₀,a₁,…,a_i,…} и {q₀,q₁,…,q_j,…}, и будем считать, что внешние алфавиты и алфавиты внутренних состояний всех машин Тьюринга берутся из этих множеств. Причем будем считать, что буква a₀ принадлежит всем внешним алфавитам машин и интерпретируется как пустой символ, а буквы q₀ и q₁ содержатся во всех алфавитах внутренних состояний всех машин и всегда означают заключительное и начальное состояние. Опишем теперь единый способ представления информации о машинах с помощью кодирования. Каждому символу из множества {L,R,E,a₀,a₁,…,a_i,…,q₀,q₁,…,q_j,…}, поставим в соответствие двоичный набор согласно таблице

	Символ	Код	Число нулей в коде
Символы сдвига	R L E	10 100 1000	1 2 3
Символы алфавита ленты	a0 a1 ... ai ...	10000 1000000 ... 10 … 0 ...	4 6 ... 2i + 4 ...
Символы алфавита состояний	q0 q1 ... qj ...	100000 10000000 ... 10 … 0 ...	5 7 ... 2j + 5 ...

Далее команде I машины Т вида qa ® q¢a¢d ставится в соответствие

Код (I) = Код(q) Код(a) Код(q¢) Код(a¢) Код(d),

представляющее собой приписывание кодов символов друг к другу. Пусть машина Т имеет алфавиты А = {a₀,a₁,…,a_m} и Q = {q₀,q₁,…,q_n}. Упорядочим пары q_ia_j лексикографически q₁a₀, q₁a₁,…, q₁a_m, q₂a₀,…, q_na₀,…, q_na_m. В соответствии с этим упорядочим команды машины Т

I₁, I₂, …, I_n(m+1).

Машине Т поставим в соответствие код

Код(Т) = Код(I₁) Код(I₂) … Код(I_n(m+1)),

получаемый приписыванием друг к другу кодов команд. Для машины Т рассмотренного примера (1.3) кодом будет

Код (Т) = 10⁷10³10⁵10⁶10³10⁷10⁶10⁷10⁶10.

Ясно, что по коду команды и коду машины команда и машина восстанавливаются однозначно. Более того, этот процесс перехода от машины к ее коду и обратно алгоритмический. Далее, код (Т) есть слово из нулей и единиц, и поэтому его можно рассматривать как двоичную запись натурального числа. Данное число называется номером машины Т. Поскольку все коды начинаются с единицы, то разным кодам соответствуют разные числа. Упорядочим машины Тьюринга по возрастанию их номеров и получим нумерацию машин Тьюринга

Т₀, T₁, T₂, …, T_n, …

Поскольку кодирование эффективно, то существует машина Тьюринга, которая по натуральному числу n выдает Код(Т_n) (если такая существует) и обратно, по Код(T_n) выдает ее номер n_T. Пусть f_n(x) - функция, вычисляемая машиной Т_n. Тогда получаем нумерацию всех вычислимых по Тьюрингу функций одного переменного

f₀(x), f₁(x), … f_n(x), …

Нетрудно показать, что всякая вычислимая по Тьюрингу функция встречается в этом списке бесконечное число раз.

Данная проблема заключается в следующем. Будем рассматривать машины Тьюринга, которые во внешнем алфавите ленты имеют 0, 1. Пусть на ленту машины Тьюринга Т записан ее код Код(Т) и машина запущена в начальном состоянии q₁. Если после конечного числа шагов машина Т остановится, то она называется самоприменимой, в противном случае - несамоприменимой. Легко привести примеры самоприменимых и несамоприменимых машин. Проблема самоприменимости состоит в том, чтобы по всякой машине Тьюринга Т (точнее по ее коду Код(Т)) установить, является ли она самоприменимой или нет. Будем говорить, что машина Тьюринга Т₀ решит проблему самоприменимости, если для любой машины Т конфигурацию q₁Код(Т) она переводит в конфигурацию q₀1, если Т самоприменима, и в конфигурацию q₀0, если Т - несамоприменима.

Теорема 1.1. Не существует машины Тьюринга Т₀, которая решает проблему самоприменимости.

¨ Допустим, что существует машина T₀, решающая проблему самоприменимости. Построим машину T₁, в которой вместо состояния q₀ введем новое заключительное состояние q₀¢ и добавим к программе машины T₀ новые команды

q₀ 1 ® q₀ 1 E,

q₀ 0 ® 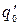0 E. (1.4)

Машина T₁ построена по машине T₀ вполне конструктивными средствами, она обладает свойствами применимости к кодам несамоприменимых машин и не применима к кодам самоприменимых машин. Действительно, если Т₁ - самоприменима, то q₁Код(Т₁) переходит в q₀1 и согласно (1.4) q₀1 Þ q₀1 и T₁ никогда не остановится. Если T₁ - несамоприменима, то q₁Код(Т) переходит в q₀0 и согласно (1.4) q₀0 Þ q₀¢0 и машина Т₁ остановится. Применим теперь машину T₁ к конфигурации q₁Код(Т₁). Если T₁ самоприменима, то по построению она не применима к коду самоприменимых машин. Если T₁ несамоприменима, то она применима к коду самоприменимых машин. Полученное противоречие показывает, что допущение о существовании машины Тьюринга T₀, решающей проблему самоприменимости, неверно. ¨

В силу тезиса Тьюринга невозможность построения машины Тьюринга означает отсутствие алгоритма решения данной проблемы. Поэтому данная теорема дает первый пример алгоритмически неразрешимой проблемы.

Отсюда вытекает еще пример алгоритмически неразрешимой проблемы - проблемы останова. Она состоит в том, чтобы по машине Т и начальной конфигурации q₁a узнать, остановится ли Т через конечное число шагов.

Проблема останова алгоритмически неразрешима. Если бы она была алгоритмически разрешимой, то взяв в качестве a код машины Т, можно было бы решить проблему самоприменимости. Данные теоремы лежат в основе доказательства алгоритмической неразрешимости большого числа алгоритмических проблем. При истолковании утверждений, связанных с алгоритмической неразрешимостью, следует иметь в виду следующее обстоятельство. Речь идет об отсутствии единого алгоритма, решающего данную проблему, при этом не исключается возможность ее решения в частных случаях.

Неразрешимость проблемы останова можно интерпретировать как несуществование общего алгоритма для отладки программ, точнее, алгоритма, который по тексту любой программы и данным для нее определял бы, зациклится ли программа на этих данных или нет.

Приведем без доказательства важную теорему теории алгоритмов.

Теорема 1.2 (теорема Райса). Никакое нетривиальное свойство вычислимых по Тьюрингу функций не является алгоритмически разрешимым.

Переформулируем эту теорему в более точном виде: Пусть С - любой класс вычислимых по Тьюрингу функций одного переменного, нетривиальной в том смысле, что имеются вычислимые функции, как входящие в С, так и не входящие в С. Тогда не существует алгоритма, который бы по номеру x функции f_x определял бы принадлежность f_x классу С.

Из данной теоремы следует, что по номеру вычислимой функции нельзя узнать, является ли она постоянной, периодической, ограниченной и т.п. Смысл данной теоремы в том, что по описанию алгоритма нельзя узнать о свойствах функций, которую он вычисляет. Подчеркнем, что “нельзя узнать” означает “не существует единого алгоритма решения”. Свойства подклассов вычислимых функций могут оказаться разрешимыми.

Дата добавления: 2014-12-08