Проверочные вопросы и упражнения

1. Сформулируйте основные требования к алгоритмам и покажите, что этим требованиям удовлетворяет метод сложения двух целых чисел.

2. Постройте детерминированную машину Тьюринга, которая применима к любому входному слову.

3. Выделите сходства и различия детерминированной машины Тьюринга и недетерминированной машины Тьюринга.

4. Покажите, что всякую детерминированную машину Тьюринга можно рассматривать как частный случай недетерминированной машины Тьюринга.

5. Приведите примеры:

а) детерминированной машины Тьюринга;

б) недетерминированной машины Тьюринга.

Характеристики сложности вычислений. Класс Р

1. Ранее была рассмотрена лишь принципиальная возможность алгоритмического решения задачи и не обращалось внимание на ресурсы времени и памяти. Однако нетрудно понять, что принципиальная возможность алгоритмического решения еще не означает, что оно может быть получено. В данном разделе рассматривается круг вопросов, связанных со сложностью вычислений. Ясно, что выбор вычислительной модели, реализующей алгоритмы, существенно влияет на сложность вычислений. Однако имеется ряд фактов, которые не зависят от вычислительной модели. Введем необходимые определения, отправляясь от машины Тьюринга в качестве модели вычислительного устройства. Пусть машина Тьюринга Т вычисляет функцию f(x). Введем функцию t_T(x), равную числу тактов работы машины Т при вычислении f(x), если значение f(x) определено. Если значение f(x) не определено, то значение t_T(x) также считается неопределенным. Функция t_T(x) называется временной сложностью. Активной зоной при работе машины Т на аргументе x называется множество всех ячеек ленты, которые посещались в процессе вычисления f(x) головкой машины. Определим функцию s_T(x) равную длине активной зоны при работе машины Т на аргументе x, если f(x) определено. В противном случае значение s_T(x) считаем неопределенным. Функцию s_T(x) называют емкостной сложностью.

Теорема 2.1. Пусть машина Т имеет внешний и внутренний алфавит мощности k и r соответственно.

Тогда справедливы оценки

s_T(x) £ ½ x ½ + t_T(x),

t_T(x) £ . (2.1)

¨ В начальный момент на ленте записан аргумент x, имеющий длину ½ x ½. На каждом шаге активной становится не более одной новой ячейки, поэтому

s_T(x) £ ½ x ½ + t_T(x).

Найдем теперь число различных конфигураций

К = a⁽¹⁾…a^(i-1)q_ja⁽ⁱ⁾…a^(s¢), s¢ £ s,

с активной зоной, не большей s. Имеется k ^s¢ £ k^s вариантов записи на ленте, r вариантов выбора состояния, s¢ £ s вариантов выбора положения головки и s вариантов для значения длины s¢ конфигурации К. Таким образом, число рассматриваемых конфигураций не превосходит rs²k^s. Если в процессе работы встретятся две одинаковые конфигурации, то машина зациклится, поскольку конфигурация однозначно определяет следующую за ней.

Поэтому, если машина в процессе вычисления использует зону s_T(x), то число ее шагов оценивается числом различных конфигураций с зоной не выше s_T(x). В итоге

t_T(x) £ .¨

Для того, чтобы иметь характеристики сложности, не зависящие от входа, удобно ввести функции

t_T(n) = ,

s_T(n) = . (2.2)

Они также называются функциями временной и емкостной сложности (в худшем случае). Поведение этих функций в пределе при увеличении размера задачи называется асимптотической временной (соответственно - емкостной) сложностью. Для конкретных задач, как правило, находятся асимптотические функции сложности. Для неотрицательных функций пишут f(n) = O(g(n)), если f(n) £ c×g(n) для некоторой константы c и всех n, начиная с некоторого. Измерение предельных потребностей времени и памяти имеет те преимущества, что порядок роста мало зависит от конкретной ЭВМ, длины представления данных различных типов и т.п. Асимптотическая сложность позволяет видеть, как растут потребности времени и памяти при росте размера входа. Например, путь некоторый алгоритм А имеет временную сложность t_A(n) = O(n²). Тогда удвоение размера входа учетверяет используемое время. Кроме того, асимптотическая сложность алгоритма определяет максимальный размер задач, разрешимых данным алгоритмом.

Например, пусть имеются три алгоритма A₁, A₂, A₃ с временной сложностью 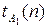= O(n), = O(n³), = O(2ⁿ). Пусть L₁, L₂, L₃ - максимальные размеры задач, решаемых алгоритмами A₁, A₂, A₃ на фиксированной универсальной ЭВМ. Предположим теперь, что для реализации алгоритмов A₁, A₂, A₃ используется ЭВМ с производительностью в 1000 раз большей, чем у предыдущей ЭВМ. Тогда нетрудно видеть, что максимальный размер решаемой задачи станет равным 1000L₁, 10L₂, L₃+9,6.

2. Мы определили функции временной и емкостной сложности для машин Тьюринга. Однако сложность вычисления на машинах Тьюринга мало соответствует затратам времени и памяти при вычислении на реальных ЭВМ. Если зафиксировать любую другую универсальную вычислительную модель, то функции временной и емкостной сложности будут корректно определены. В настоящее время для оценок сложности алгоритмов используются различные модели вычислительных устройств, но наиболее важной среди них является машина с произвольным доступом к памяти (МПД). Машина с произвольным доступом к памяти является моделью вычислительной машины с одним процессором (сумматором), в котором команды программы не могут себя изменять. МПД состоит из входной ленты, с которой считываются входные данные, выходной ленты, на которой записываются результаты, и памяти. Входная лента представляет собой последовательность ячеек, в каждой из которых может быть записано целое число. В каждом такте считывающая головка считывает содержимое одной ячейки и сдвигается на одну ячейку вправо. Выходная лента также состоит их таких же ячеек, которые в начале вычисления пусты. При выполнении команды в ячейке выходной ленты, обозреваемой головкой машины, записывается результат. Как только выходной символ записан, его нельзя изменять. Память состоит из последовательности регистров R₀, R₁, R₂,…, каждый из которых способен хранить произвольное целое число. На число регистров не накладывается никаких ограничений. Такая идеализация оправдана, если размер задачи достаточно мал, либо используемые в процессе вычисления числа малы. Программа МПД есть последовательность команд. Она не записывается в память и не может себя изменять. Множество используемых команд соответствуют тем, которые используются в современных ЭВМ, в частности, арифметические операции, операции пересылки, косвенная адресация, команды ветвления, логические операции. Все операции проводятся в регистре R₀, называемом сумматором. Приведем блок-схему МПД

x1

x2

…

xn

…

Входная лента (только считывается)

Счетчик

команд Программа

R₀

R₁

R₂

.

.

.

Память

y1

y2

……

Выходная лента

(только записывается)

Машина МПД в силу своей гибкости в организации вычислительного процесса удобна для получения достаточно реалистических верхних оценок сложности алгоритмов. Основное же применение машин Тьюринга заключается в установлении нижних оценок на время и память, необходимое для решения данной задачи. Известен факт, что МПД вычисляет в точности тот же класс функций, что и машины Тьюринга. Для точного определения временной и емкостной сложности следует определить время, необходимой для выполнения каждой МПД-команды и объем памяти, используемый каждым регистром. Наиболее распространенные случаи:

1) Равномерный весовой критерий, при котором предполагается, что каждая МПД-команда требует для выполнения одну единицу времени и одну единицу памяти.

2) Логарифмический весовой критерий, при котором предполагается, что каждая МПД-программа требует на свое выполнение время, пропорциональное длине ее операндов и каждый регистр использует память, равную максимальной длине записи хранимого в нем числа. Такое предположение более реалистично, и в дальнейшем мы ограничимся рассмотрением временной сложности МПД-программ с логарифмическим весовым критерием.

Приведем факт, связанный с взаимным моделированием МПД и машинами Тьюринга.

1) Пусть данная машина Тьюринга имеет временную сложность Т(n). Тогда МПД моделирует ее за время O(Т(n)logТ(n)) (при логарифмическом весовом критерии).

2) Пусть данная МПД имеет временную сложность Т(n). Тогда машина Тьюринга моделирует ее за время O(Т⁴(n)).

3. Алгоритмом полиномиальной сложности называется алгоритм, имеющий временную сложность вида O(p(n)), где p(n) - некоторый полином, n - размер входа. Алгоритм, не являющийся алгоритмом полиномиальной сложности, называется алгоритмом экспоненциальной сложности. Поскольку МПД и машины Тьюринга моделируют друг друга с полиномиальным временем, то полиномиальный алгоритм в одной модели будет полиномиальным и в другой. Обозначим через Р - класс задач, для которых существуют разрешающие алгоритмы полиномиальной сложности. Класс Р определяется однозначно, если рассматривать и другие универсальные алгоритмические модели. Полиномиальные алгоритмы обладают рядом положительных свойств: 1. Любой полиномиальный алгоритм более эффективен при достаточно больших размерах входа, чем экспоненциальный. 2. Полиномиальные алгоритмы лучше реагируют на рост производительности ЭВМ. Это следует из примера п.1, где рассматривался вопрос об увеличении размера решаемой задачи при увеличении производительности ЭВМ. 3. Полиномиальные алгоритмы обладают свойством “замкнутости”: можно комбинировать полиномиальные алгоритмы, вызывать полиномиальные алгоритмы в качестве “подпрограммы”, при этом результирующий алгоритм останется полиномиальным. Заметим, что при практической применении алгоритмов следует учитывать фактическое поведение сложности, например О(n¹⁰⁰⁰) при практических значениях n ведет себя хуже, чем O(2ⁿ). На практическое использование влияет также и значение соответствующих констант. В настоящее время общепринят тезис, согласно которому класс Р отождествляется с классом эффективно решаемых задач. Соответственно задачи, не принадлежащие классу Р, называются труднорешаемыми. Легко заметить, что классу Р принадлежат многие рассмотренные в данном курсе задачи: умножение и транзитивное замыкание бинарных отношений, связность, эйлеровость, кратчайший путь в графе между парой вершин, обратимость и регулярность автомата (при табличном задании) и другие задачи.

Рассмотрим задачу о проверке функциональной полноты системы булевых функций. Пусть каждая булевая функция f(x₁,…,x_n) данной системы кодируется строчкой своих значений:

f(0,...,0)f(0,...,0,1)...f(1,1,...,1).

Например, функция f(x₁,x₂) = x₁×x₂ задается строкой 0001, т.к.

f(0,0) = 0, f(0,1) = 0, f(1,0) = 0, f(1,1) = 1.

Системы функций будем кодировать таким образом: каждая функция задается своим кодом, а коды разных функций отделены разделительным знаком (*). Например, система x₁×x², 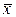, x₁Úx₂ закодируется так:

0001 * 10 * 0111.

Рассмотрим функцию p(x), определенную на словах в алфавите {0,1,*} следующим соотношением:

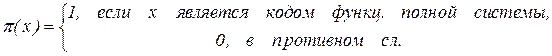
Справедлив факт, который мы приведем без доказательства (Трахтенброт Б.А., Бардзинь Я.М.).

Теорема 2.2. 1. Существует машина Тьюринга Т, вычисляющая функцию p(x) с временной сложностью t_T(x) £ c₁ ½ x ½ ², где с₁ - некоторая константа.

2. Для любой машины Тьюринга Т, вычисляющей функцию p(x), существует константа c₂ такая, что для всех n, больших некоторого n₀, временная сложность t_T(n) удовлетворяет неравенству

t_T(n) > c₂ n².

Таким образом, задача проверки функциональной полноты принадлежит классу Р при табличном кодировании булевых функций.

Если данную задачу кодировать формулами, то не известно, существует ли полиномиальный разрешающий алгоритм.

4. Определим время работы недетерминированной машины, положив (если x - принимается)

= + ,

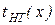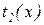где - время работы на стадии 1, т.е., по определению, = ,

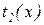- время работы на стадии 2, т.е., по определению, 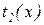= (Т - соответствующая (обычная) машина Тьюринга).

Определим

= .

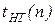Недетерминированная машина решает задачу П за полиномиальное время, если

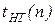= O (p (n))

для некоторого полинома р.

Заметим, что временная функция определена только для тех индивидуальных задач x, которые принимаются НДМТ.

Дата добавления: 2014-12-08