Модель сопряжения элементов 1 страница

Математическая модель сложной системы помимо формального описания элементов обязательно включает формальные описания взаимодействия элементов – модель сопряжения.

В модели сопряжения элементов отражается не процесс функционирования элементов, а только такие их свойства, которые существенны для сопряжения элементов системы друг с другом и с внешней средой.

Основные предположения, концентрирующие интуитивные представления о закономерностях сопряжения элементов системы.

1. Взаимодействие между системой и внешней средой, а также между агрегатами внутри системы осуществляется посредством передачи сигналов, взаимное влияние вне механизма обмена сигналами не учитывается. Внешняя среда рассматривается как некоторый фиктивный агрегат, характеризуемый совокупностью входных и выходных сигналов.

2. Сигнал описывается конечным набором характеристик как совокупность элементарных сигналов, одновременно возникающих на входе элемента (аналогично и выходной сигнал). Любой сигнал можно характеризовать конечным числом параметров (для детали – размеры, материал, температура, для информационного сигнала – совокупность букв, цифр). Элементарные сигналы передаются независимо друг от друга по элементарным каналам. Каждому контакту соответствует один элементарный канал.

3. К каждому из входных контактов элемента подключается не более, чем один элементарный канал (исключается неопределенность в поведении элемента, если к нему будут приходить несколько элементарных каналов от различных выходных контактов).

Каждый элемент С_j, в том числе С₀, как элемент системы S достаточно характеризовать множеством входных контактов X₁^(j), X₂^(j),..., X_i^(j),..., X_m^(j), которое обозначим [X_i^(j)]₁^m, и множеством выходных контактов Y₁^(j), Y₂^(j),..., Y_k^(j),..., Y_r^(j), обозначаемым [Y_l^(j)]₁^r. Здесь для простоты приняты обозначения m = m_j, r = r_j.

Таким образом, математической моделью элемента С_j, используемой для формального описания сопряжения его с прочими элементами и внешней средой, является пара множеств [X_i^(j)]₁^m, [Y_l^(j)]₁^r.

Множество всех входных контактов всех элементов системы и внешней среды - 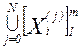. Множество выходных контактов - .

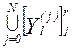Каждому входному контакту X_i^(j) соответствует не более чем один выходной контакт Y_l^(k), с которым он связан элементарным каналом. Поэтому можно ввести однозначный оператор

Y_l^(k) = R (X_i^(j)) с областью определений в множестве 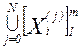и областью значений в множестве 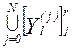, сопоставляющий входному контакту X_i^(j) выходной контакт Y_l^(k), связанный с ним элементарным каналом.

Совокупность множеств 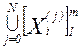и 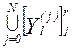и оператора R называется схемой сопряжения, оператор R – оператором сопряжения.

Оператор сопряжения можно задать в виде таблицы, в которой на пересечении строк с номерами элементов системы j и столбцов с номерами контактов i, располагаются пары чисел (k, l), указывающие номер элемента к и номер элемента l, с которыми соединен контакт X_i^(j).

На рисунках изображены пример агрегативной системы и оператора сопряжения в виде таблицы, возможная схема сопряжения подсистем агрегативной системы.

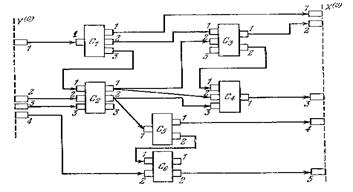
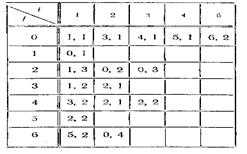
Возможная схема сопряжения элементов агрегативной системы и оператор сопряжения

Сложная система S может быть расчленена на некоторое число подсистем S_μ, μ = 1, 2,..., M, содержащих не менее чем по одному элементу таким образом, что данный элемент C_j входит только в одну из подсистем S_μ. Подсистема S_μ сама является сложной системой и в то же время – элементом системы S. Подсистема S_μ как самостоятельная система должна иметь контакты X_i^(0)μ и Y_l^(0)μ фиктивного элемента С₀^μ, представляющего внешнюю среду для нее, а как элемент системы S она должна содержать входные X_i^(μ) и выходные Y_l^(μ) контакты для связи с другими подсистемами. Соответствующие X_i^(μ) и Y_j^(0)μ, а также X_i^(0)μ и Y_l^(μ) объединяются в двойные контакты на границах подсистемы S_μ.

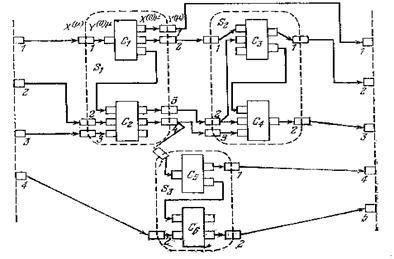
Возможная схема сопряжения подсистем агрегативной системы

Методика сопряжения связей между элементами сложной системы при помощи операторов сопряжения распространяется и на те случаи, когда в процессе функционирования системы структура связей изменяется во времени или подчиняется внешним командам управления. В этом случае в оператор сопряжения входит время t и параметр a (сигнал) управления.

6 МАТЕМАТИЧЕСКИЕ МОДЕЛИ РАСПРЕДЕЛЕНИЯ РЕСУРСОВ В ИССЛЕДОВАНИИ ОПЕРАЦИЙ

6.1 Моделирование операций распределения ресурсов

При выборе концепции системы возникают задачи выбора решений (действий) - оптимальной организации взаимодействия элементов, определения оптимальных режимов функционирования системы и ее элементов в различных условиях внешней среды - задачи выбора способа действия, т.е. целенаправленного функционирования системы. Такие задачи возникают при распределении ресурсов системы - варианта плана применения системы, организации производства и снабжения, эксплуатации транспортных систем, параметров конструкции, выбора средств производства, вооружения, в здравоохранении, бытовом обслуживании, связи, при боевых действиях и т.д.

Любое целенаправленное действие называется операцией. В общем случае – это совокупность взаимосвязанных действий всех компонентов системы, направленных на решение поставленной задачи.

Модель операции (операционная модель - формализованное описание факторов и связей между ними, отражающих ход операции) представляет собой совокупность, состоящую из субъекта, формирующего цель операции (оперирующей стороны), запаса активных средств (ресурсов) для проведения операции, набора стратегий, т.е. способов использования этих ресурсов, и критерия для сравнения различных стратегий достижения цели операции.

Модель операции разрабатывается на основе схемы операции, представленной в виде ряда последовательных этапов и элементарных действий компонентов для решения поставленной задачи (выполнения цели системы).

Степень соответствия результата операции поставленной ей цели (задаче) характеризуется критерием эффективности, который может зависеть от всех факторов, входящих в модель операции, в том числе, и неопределенных.

И управления, и неопределенные факторы могут быть функциями различной природы и сложности в зависимости от конкретных условий проведения операции, информированности оперирующей стороны.

Основная задача исследования операций – принятие решения о наилучшем способе достижения цели - выбор программы действий (способов использования ресурсов на выполнение операции) – решается методами математического программирования.

Основные разделы теории исследования операций: математическое программирование (линейное и нелинейное, детерминированное и стохастическое), теория принятия решений и теория игр, теория управления запасами, теория массового обслуживания, имитационное моделирование. Выбор метода решения диктуют тип и сложность исследуемой математической модели.

Степень соответствия результата операции поставленной ей цели (задаче) характеризуется критерием эффективности, который может зависеть от всех факторов, входящих в модель операции, в том числе, и неопределенных.

Общая модель операции выработки решения состоит из взаимосвязанных моделей: модели процесса операции (включая модель управляемой системы и модель обстановки проведения операции) и модели принятия решения. При этом учитываются физические и критериальные ограничения.

Физические ограничения ни при каких обстоятельствах не могут быть нарушены, поскольку они выражают законы сохранения.

Пример физических ограничений. Обозначим через q_i норму полива – количество воды, которое мы должны направить на орошение единицы земельной площади x _i. Тогда

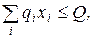
где Q - общее количество воды, которое накоплено в водохранилище.

Кроме того, суммарная площадь земли, которую можно использовать под посевы, также должна быть фиксирована, т.е. величины x _i должны удовлетворять еще одному ограничению:

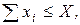
где Х – суммарная земельная площадь.

Критериальные ограничения определяются требованиями к конструкции и не являются такими жесткими – они находятся в распоряжении субъекта и в принципе могут быть нарушены или изменены.

Например, распределяя землю под посевы, необходимо добиться урожая максимальной стоимости, но при заданной структуре конечного продукта, или при проектировании самолета, кроме достижения его максимальной экономичности, могут быть ограничения на его крейсерскую скорость (не меньше заданной).

Математическое программирование – это математическая дисциплина, в которой разрабатываются методы отыскания экстремальных значений целевой функции среди множества ее возможных значений, определяемых ограничениями.

Наличие ограничений делает задачи математического программирования принципиально отличными от классических задач математического анализа по отысканию экстремальных значений функции. Методы математического анализа для поиска экстремума функции в задачах математического программирования оказываются непригодными.

Содержание математического программирования составляют теория и методы решения задач о нахождении экстремумов функций на множествах, определяемых линейными и нелинейными ограничениями (равенствами и неравенствами). В этом и состоит специфика задач математического программирования: множество условий задается не системой уравнений, а системой неравенств, чаще всего экстремум достигается на границах множества условий, где нарушается принцип дифференцируемости, в практических задачах число переменных столь велико, что приводит к необходимости применения аналитических методов или эффективных вычислительных способов получения приближенного решения.

Методы математического программирования используются в экономических, организационных, военных и др. системах для решения так называемых распределительных задач. Распределительные задачи возникают в случае, когда имеющихся в наличии ресурсов не хватает для выполнения каждой из намеченных работ эффективным образом и необходимо наилучшим образом распределить ресурсы по работам в соответствии с выбранным критерием оптимальности.

Классификация задач математического программирования.

В математическом программировании выделяют два направления – решение детерминированных (вся исходная информация определена) и стохастических (параметры носят случайный характер с известными вероятностными характеристиками) задач.

В зависимости от свойств целевой функции и функции ограничений все задачи математического программирования делятся на два основных класса:

- задачи линейного программирования,

- задачи нелинейного программирования.

Линейное программирование – целевая функция линейна, а множество, на котором ищется экстремум целевой функции, задается системой линейных равенств и неравенств. В линейном программировании существуют классы задач, структура которых позволяет создать специальные эффективные методы их решения (например, транспортные задачи).

Нелинейное программирование – нелинейны целевая функция и ограничения. Здесь выделяют: выпуклое программирование (выпукла целевая функция и множество, на котором решается экстремальная задача), квадратичное программирование (целевая функция квадратична, а ограничения – линейные равенства и неравенства).

Целочисленное линейное программирование ориентировано на решение задач линейного программирования, в которых все или некоторые переменные должны принимать целочисленные (или дискретные) значения.

Формулировка задачи математического программирования

Задачи математического программирования, как правило, содержат большое число переменных и ограничений и не всегда допускают умозрительный анализ. Здесь требуется тщательная формализация и включение в математическую модель всех сколько-нибудь существенных ограничений.

Прежде чем построить математическую модель задачи, необходимо четко разобраться с ситуацией, описанной в условии. Для этого необходимо с точки зрения заданной задачи, а не математики, ответить на следующие вопросы:

1) Что является искомыми величинами задачи?

2) Какова цель решения? Какой параметр задачи служит критерием эффективности (оптимальности) решения, например, прибыль, себестоимость, время и т.д. В каком направлении должно изменяться значение этого параметра (к max или к min) для достижения наилучших результатов?

3) Какие условия в отношении искомых величин и ресурсов задачи должны быть выполнены? Эти условия устанавливают, как должны соотноситься друг с другом различные параметры задачи, например, количество ресурса, затраченного при производстве, и его запас на складе; количество выпускаемой продукции и емкость склада, где она будет храниться; количество выпускаемой продукции и рыночный спрос на эту продукцию и т.д.

После предварительной постановки задачи получают ее формальное решение для простейших случаев, на которых можно проанализировать корректность поставленной задачи. На основании такого анализа вводятся дополнительные параметры и ограничения, проверяется корректность отнесения задачи к тому или иному классу, корректность введения линейности.

Общая схема формализации на основании содержательного описания задачи:

1.Определение переменных задачи (основных параметров).

2. Определение управляющих переменных, характеризующих существо действий и их элементарных составляющих.

3. Формулировка критериев эффективности через параметры и управляющие переменные.

4. Определение ограничений (области допустимых решений) через переменные задачи.

Задача математического программирования содержит n переменных x_i (i =1, 2,..., n), образующих n -мерный вектор переменных х.

На переменные накладываются ограничения - в форме равенств h_i (x) = 0, i = 1,..., p или неравенств g_i (x) ≥ 0, i = 1,..., q.

f (x) – целевая функция (в общем случае нелинейная) всех или некоторых переменных x_i (i =1, 2,..., n).

Задача математического программирования формулируется следующим образом:

Минимизировать (или максимизировать) f (x) при условиях g_i (x) ≥ 0, i = 1,..., q; h_i (x) = 0, i = 1,..., p. Или кратко Min { f (x)│ g_i (x) ≥ 0, i = 1,..., q; h_i (x) = 0, i = 1,..., p }.

6.2 Модели линейного программирования

Линейное программирование применяется при решении задач оптимального распределения ресурсов, управления и планирования производства; определения оптимального размещения оборудования; оптимального плана перевозок груза (транспортная задача) и т.д.

По оценкам американских экспертов около 75% от общего числа применяемых оптимизационных методов приходится на линейное программирование. Около четверти машинного времени, затраченного в последние годы на проведение научных исследований, было отведено решению задач линейного программирования и их многочисленных модификаций.

Задачи линейного программирования относятся к категории оптимизационных. Они находят широкое применение в различных областях практической деятельности: при организации работы транспортных систем, в управлении промышленными предприятиями, при составлении проектов сложных систем. Многие распространенные классы задач системного анализа, в частности, задачи оптимального планирования, распределения различных ресурсов, управления запасами, календарного планирования, межотраслевого баланса укладываются в рамки моделей линейного программирования.

Несмотря на различные области приложения, данные задачи имеют единую постановку: найти значения переменных x₁, …, x_n, доставляющие оптимум заданной линейной формы z=c₁x₁ + c₂x₂+… + c_nx_n при выполнении системы ограничений, представляющих собой также линейные формы.

В задачах линейного программирования критерий эффективности и функции в системе ограничений линейны.

Если содержательный смысл требует получения решения в целых числах, то такая задача является задачей целочисленного программирования.

Если в задаче математического программирования имеется переменная времени, а критерий эффективности выражается через уравнения, описывающие течение операций во времени, то такая задача является задачей динамического программирования.

При описании реальной ситуации с помощью линейной модели следует проверять наличие у модели свойств пропорциональности, аддитивности.

Основные допущения при построении линейных моделей:

- пропорциональность;

- аддитивность;

-. неотрицательность (не может быть отрицательного объема производства).

Пропорциональность - затраты ресурсов пропорциональны объему производства - вклад каждой переменной в целевой функционал и общий объем потребления соответствующих ресурсов должен быть прямо пропорционален величине этой переменной.

Например, если, продавая j -й товар в общем случае по фиксированной цене, фирма будет делать скидку при определенном уровне закупки до более низкого уровня цены, то будет отсутствовать прямая пропорциональность между доходом фирмы и количеством проданного товара. Т.е. в разных ситуациях одна единица j-го товара будет приносить разный доход.

Аддитивность означает, что целевой функционал и ограничения должны представлять собой сумму вкладов от различных переменных. Величина, соответствующая целому объему всегда равна сумме величин, соответствующих его частям при любом способе разбиения на части.

Примером нарушения аддитивности служит ситуация, когда увеличение сбыта одного из конкурирующих видов продукции, производимых одной фирмой, влияет на объем реализации другого.

Решение практической задачи нельзя считать законченным, если найдено оптимальное решение. Некоторые параметры задачи (финансы, запасы сырья, производственные мощности и др.) можно регулировать, что, в свою очередь, может изменить найденное оптимальное решение. Эта информация получается в результате выполнения анализа чувствительности. Анализ чувствительности позволяет оценить влияние этих параметров на оптимальное решение. Если обнаруживается, что оптимальное решение можно улучшить за счет небольших изменений заданных параметров, то целесообразно реализовать эти изменения.

Формулировка общей задачи линейного программирования.

Необходимым условием постановки задачи линейного программирования являются ограничения на наличие ресурсов, величину спроса, производственную мощность предприятия и другие производственные факторы.

Каждая совокупность значений переменных (аргументов функции f), которые удовлетворяют системе ограничений, называется допустимым планом задачи линейного программирования. Функция f, максимум или минимум которой определяется, называется целевой функцией задачи. Допустимый план, на котором достигается максимум или минимум функции f, называется оптимальным планом задачи.

Задачей линейного программирования является выбор из множества допустимых планов наиболее выгодного (оптимального).

В общей постановке задача линейного программирования выглядит следующим образом:

Нужно определить максимум или минимум линейной целевой функции (линейной формы)

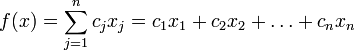
при ограничениях в виде равенств или неравенств

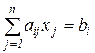, i = 1,..., r;

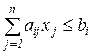, i = r+1,..., g;

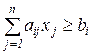, i = g +1,..., m;

x_ij ≥ 0 - требование неотрицательности управляющей переменной

где x _j, j =1,..., n – управляющие переменные, или решения задачи,

b _i, a _ij, i =1,..., m, j =1,..., n – параметры,

f – целевая функция.

Задача содержит n переменных и m ограничений.

Множество точек, удовлетворяющих системе ограничений, называется допустимым множеством (областью). Любая точка этого множества называется допустимой точкой (решением, планом). Линейная функция называется целевой функцией. Допустимая точка, которая минимизирует (максимизирует) функцию цели, называется оптимальным планом – решением задачи линейного программирования.

В канонической форме задача является задачей на максимум (минимум) некоторой линейной функции F, ее система ограничений состоит только из равенств (уравнений). При этом переменные задачи х₁, х₂,..., х_n являются неотрицательными:

Естественным решением сформулированной задачи линейного программирования является метод простого перебора: найти произвольное решение х ₁ в допустимой области, вычислить (с, х ₁), затем найти другое решение х ₂, вычислить (с, х ₂) и т.д. и среди полученных значений целевой функции (с, х) выбрать наименьшее. Этот путь перебора оказывается нереализуемым в связи со сложностью поиска допустимых решений, (допустимая область решений имеет бесконечное множество точек) и невозможностью поиска всех допустимых решений. Для решения задач линейного программирования строятся такие схемы поиска, которые позволяют выбирать оптимальный план, не перебирая всех возможных вариантов.

Типовые задачи линейного программирования

Методы линейного программирования позволяют описать широкий круг задач коммерческой деятельности, таких, как: планирование товарооборота; размещение розничной торговой сети города; планирование товароснабжения города, района; прикрепление торговых предприятий к поставщикам; организация рациональных перевозок товаров (транспортная задача); распределение работников торговли по должностям (задача о назначении); организация рациональных закупок продуктов питания (задача о диете); распределение ресурсов; планирование капиталовложений; оптимизация межотраслевых связей; замена торгового оборудования; определение оптимального ассортимента товаров в условиях ограниченной площади; установление рационального режима работы.

Транспортная задача.

Транспортные модели описывают перемещение (перевозку) какого-либо товара из пункта отправления (исходный пункт, например место производства) в пункт назначения (склад, магазин, грузохранилище). Назначение транспортной задачи — определить объем перевозок из пунктов отправления в пункты назначения с минимальной суммарной стоимостью перевозок. При этом должны учитываться ограничения, налагаемые на объемы грузов, имеющихся в пунктах отправления (предложения), и ограничения, учитывающие потребность грузов в пунктах назначения (спрос). В транспортной модели предполагается, что стоимость перевозки по какому-либо маршруту прямо пропорциональна объему груза, перевозимого по этому маршруту. От того, насколько рационально будет прикрепление пунктов потребления к пунктам производства, зависит объем транспортной работы.

В качестве критерия оптимальности можно принять минимальную стоимость перевозок всего груза (общие транспортные расходы), либо минимальное время его доставки. Рассмотрим задачу с первым критерием.

Возникает задача о наиболее рациональном прикреплении потребителей к поставщикам, при котором удовлетворяются их потребности, а суммарные затраты на перевозку минимальны. При этом величина транспортных расходов прямо пропорциональна объему перевозимой продукции и задается с помощью тарифов на перевозку единицы продукции.

Параметры задачи.

Имеется m пунктов производства А₁, …, А _m однородного продукта и n пунктов потребления В₁,…, В _n.

Предложение поставщика в каждом i -м пункте составляет а_i единиц, i = 1,..., m.

Спрос потребителя в каждого j -ом пункте составляет b_j единиц, j = 1,.... n.

Транспортные расходы на перевозку единицы продукции из А _i в В _j составляет c_ij (себестоимость, расстояние, тариф, время, расход топлива).

Требуется определить оптимальный план перевозок, при котором суммарные транспортные расходы минимальны продукции (управляющий параметр - количество продукции, перевозимой от каждого поставщика к каждому потребителю).

Обозначим x_ij – количество продукции, перевозимой от i -го поставщика j -му потребителю

i = 1,..., m, j = 1,.... n.

Математическая модель задачи

Суммарные затраты на транспортировку из всех пунктов производства во все пункты потребления:

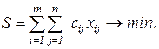тр

Управляющий параметр: x_ij ≥ 0 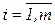, 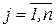- количество единиц продукции, поставляемой из А _i в В _j – перевозки из пунктов потребления в пункты производства исключены.

Ограничения

Суммарное предложение должно быть не меньше суммарного спроса

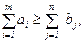
В каждый пункт потребления доставляется продукции не менее необходимой

,

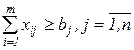От каждого поставщика вывозится продукции не более имеющейся

.

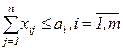Всякое неотрицательное решение систем уравнений называется опорным планом (совокупность чисел x_ij, 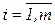, , 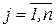удовлетворяющая приведенным ограничениям). Решение X*=(x_ij ), при котором функция S принимает минимальное значение - называется оптимальным планом транспортной задачи.

Дата добавления: 2014-11-29