Перевозка неоднородного продукта на разнородном транспорте

Для обеспечения перевозок может быть использовано s автохозяйств, в каждом из которых r типов автомашин. Машины разных типов, обладая различными эксплуатационными характеристиками и разной скоростью, могут доставлять любой из m грузов каждому из n потребителей.

Расстояние от места расположения g -го автохозяйства (g = 1,…., s) до пункта производства i -го груза (i = 1,…, m) известно. Известна скорость машин к -го типа (к = 1, …, r) для всех маршрутов. Известно время погрузки и разгрузки машин каждого типа в каждом пункте назначения. С учетом этой информации можно определить t_ijgk время занятости одной машины к -го типа g -го автохозяйства на работах по перевозке i -го груза j -му потребителю (или любые другие виды затрат, связанные с перевозкой единицы i -го груза в j -ый пункт назначения на одной машине к -го типа из g -го автохозяйства).

Параметры модели

a _gк – количество машин к -го типа в g -ом автохозяйстве;

c_ij – число единиц i -го груза, подлежащего перевозке j -му потребителю;

d_ij – число единиц i -го груза, которое перевозится в j -ый пункт назначения на одной машине (определяется по известной грузоподъемности машин).

Учет различной грузоподъемности машин приводит к распределительной задаче.

Требуется определить, сколько машин того или иного типа из какого автохозяйства следует направить для удовлетворения спроса каждого потребителя в каждом виде груза при минимальных суммарных затратах на перевозки (в автомобилечасах).

Примем х_ijgk – количество машин к -го типа из g -го автохозяйства, предназначенных для перевозки i -го груза j -му потребителю.

Математическая модель.

Определить значения переменных х_ijgk, на которых достигается минимум

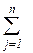
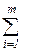
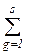
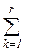t_ijgk х_ijgk → min

при условиях

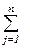
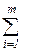х_ijgk ≤ а_gk, _, g = 1,…., s, к = 1, …, r - общее число машин к -го типа, направленных из g -го автохозяйства на перевозку всех грузов ко всем потребителям, не может превысить числа транспортных единиц к -го типа, которым располагает g -е автохозяйство;

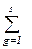
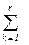d_ij х_ijgk = c_ij, i = 1,…, m, j = 1,…, n – спрос каждого пункта потребления в каждом виде груза должен быть полностью удовлетворен,

х_ijgk ≥ 0, i = 1,…, m, j = 1,…, n, g = 1,…., s, к = 1, …, r.

Полученная четырехиндексная задача путем преобразований может быть сведена к классической двухиндексной транспортной задаче достаточно общим для многих задач способом.

Каждый пункт, потребляющий m различных грузов рассматривается как группа из m различных пунктов, а автохозяйство с r типами машин учитывается как r автохозяйств. Соответственно определяются потребности каждого пункта назначения и возможности каждого транспортного подразделения.

Заменим пары индексов (i, j) и (g, к) двумя индексами λ и μ по следующим формулам:

λ = i + m (j – 1), μ = g + s (к – 1)

Когда индекс I пробегает значения 1,2, …, m, а j - значения 1,2, …, n, индекс λ принимает все целочисленные значения от 1 до mn. Индекс μ пробегает значения 1,2, …, sr.

Введем замену переменных х_ijgk = z_{λ μ} , i = 1,…, m, j = 1,…, n, g = 1,…., s, к = 1, …, r.

Обозначим t_ijgk через τ_{λ μ} , отношение c_ij / d_ij через g_λ, а_gk через b_μ.

В новых обозначениях задача сводится к вычислению переменных z_λμ, обращающих в минимум линейную форму

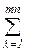
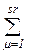τ_{λ μ} z_λμ → min

при условиях

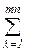z_λμ ≤ b_μ, μ = 1,2, …, sr,

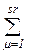z_λμ = g_λ, λ = 1,2,…, mn,

z_λμ ≥ 0, λ = 1,2,…, mn, μ = 1,2, …, sr.

Пришли к обычной транспортной задаче размеров mn х sr. По компонентам z_λμ оптимального плана задачи вычисляются составляющие х_ijgk. При этом индексы i и j вычисляются по формулам

m, если λ кратно m,

i = { остатку от деления λ на m, если λ не делится на m;

λ / m, если λ кратно m,

j = { целой части выражения (λ / m + 1), если λ не делится на m;

Аналогичным путем вычисляются индексы g и к.

7 МАТЕМАТИЧЕСКИЕ МОДЕЛИ ФИЗИЧЕСКИХ ЯВЛЕНИЙ И ПРОЦЕССОВ. универсальность моделей

7.1 Математические модели на основе фундаментальных законов

Математические модели, которые строятся на основе опытного изучения явления (феномена) – феноменологические модели. Эти модели связывают только непосредственно наблюдаемые и измеряемые в макро- опытах величины, физическая природа явления остается нераскрытой. Такие модели только описывают явления, устанавливают причинно-следственные связи, но не могут ответить на вопрос "почему?".

На феноменологической основе возникла первая крупная модель – механика Ньютона, подтвержденная экспериментальными данными. Он создал математическую модель и математически сформулировал один из фундаментальных законов природы – закон всемирного тяготения (в этом законе не ясна физическая природа сил тяготения).

Расширение феноменологической базы, накопление фактического экспериментального материала дает возможность создавать все более общие и полные модели (например, развитие механики от Ньютона к Эйнштейну).

Изучением математических моделей физических явлений занимается математическая физика. Для создания модели нет четких правил, но есть сложившийся набор приемов: учет основных фундаментальных законов, использование физических аналогий, вариационных принципов и т.д.

В физике сложилась схема построения моделей: формулируется система аксиом и совокупность правил, определяются допустимые операции над объектом, затем строится математическая модель. По мере накопления фактов модель уточняется, что дает возможность установить закономерности, предсказать течение процесса, его количественные характеристики в различных условиях.

При математическом описании физических явлений и процессов используются методы составления математических моделей: теоретический (на основе применения фундаментальных законов природы), эмпирический (экспериментaльно-стaтистический), экспериментaльно-aнaлитический (полуэмпирический), на основе аналогий, на основе вариационных принципов.

Эмпирические модели. Если процесс мало изучен и ничего не известно о его природе, используется эмпирический метод построения моделей. Этот метод тaкже позволяет получить мaтемaтическое описaние действующего объектa без исследовaния его внутренней структуры.

Построение эмпирических математических моделей основано на проведении экспериментальных исследований, связанных с наблюдением и измерением внешних проявлений свойств объекта, с последующим обобщением результатов этих измерений в алгоритмической форме или в виде аналитических зависимостей.

При построении эмпирических моделей используют понятие "черного ящика" – объект рассматривается безотносительно его внутренних свойств, т.е. без учета физической сущности протекающих в нем процессов (например, в метеорологии). Модель отрaжaет только зависимость значений выходных пaрaметров от входных.

На основании эксперимента строится приближенная модель. Подбираются аналитические зависимости, наилучшим образом согласующиеся с результатами эксперимента в точках их проведения: строится функциональная зависимость значений выходных параметров от входных.

Если такие модели построены без учета случайных ошибок (они отсутствуют или их статистические характеристики неизвестны), то приближенная модель называется эмпирической.

Если статистические характеристики случайных ошибок известны и учитываются, такая аппроксимирующая модель называется регрессионной. Уравнения регрессии строятся методом наименьших квадратов. Наиболее часто функцию представляют алгебраическими многочленами.

Экспериментально-аналитические модели - это смешанный тип математических моделей, в которых теоретические соображения качественного характера сочетаются с обработкой результатов наблюдений внешних проявлений свойств изучаемого объекта.

При использовании этого метода необходимо определить физическую сущность явлений, протекающих в объекте – в отличие от экспериментального, этот метод отражает теорию процесса. Для учета влияния явлений, не учтенных при составлении модели, вводятся эффективные коэффициенты на основе экспериментов.

Используется декомпозиция сложного явления, т.е. на основе анализа определяются более простые, элементарные процессы, которые можно исследовать более доступными способами.

После анализа влияния элементарных процессов на процесс в целом, несущественные факторы отбрасываются, и выбирается тот элементарный процесс, который оказывает наиболее существенное влияние. Затем для основного простого процесса составляется его математическое описание в виде характерной для этого процесса физической зависимости (не в форме полинома). Влияние остальных элементарных процессов учитывается изменением коэффициентов, входящих в эту зависимость.

Пример: процесс переноса тепла в неподвижном слое.

При определенных условиях (температура менее 800 К и малые линейные скорости потока газа) перенос тепла в основном определяется теплопроводностью и описывается уравнением Фурье (поток тепла пропорционален градиенту температуры): q _Т = - λdT / dx. Для учета всех составляющих процесса переноса тепла вводится экспериментальное значение коэффициента λ - некоторое "эффективное" значение λ_эф. Тогда уравнение примет вид: q _Т = - λ_эф dT / dx. Это уравнение является полуэмпирической моделью процесса переноса тепла в неподвижном слое. Коэффициент эффективности не является физической константой, a зависит от условий экспериментов, при которых она была получена и от масштабов установки.

На поверхности S тела с однородной по объему, но меняющейся во времени t температурой T (t) происходит теплообмен с окружающей средой, имеющей постоянную температуру T _с.

Примем, что плотность теплового потока от окружающей среды к телу пропорциональна разности температур q = α (T _с - T),где α - коэффициент теплоотдачи.

Подводимый к телу от окружающей среды тепловой поток

Q = qS = α (T _с - T) S.

Он вызывает изменение внутренней энергии тела, которое пропорционально скорости dT (t)/ dt изменения температуры, а коэффициентом пропорциональности служит полная теплоемкость C _T тела, равная количеству тепловой энергии, необходимой для повышения температуры тела на 1К, измеряемая в Дж/K.

C _T dT (t)/ dt = Q (t).

Скорость изменения температуры тела пропорциональна разности между температурой тела и температурой среды:

dT (t)/ dt = к (T _с - T) S, к = α / C _T – коэффициент пропорциональности.

Матмодель, описывающая изменение температуры тела во времени – ОДУ первого порядка, решение которого при α = const имеет вид

T = T _с - (T _с – T ₀) e ^{- α St / C T},

где T ₀ - температура тела в начальный момент времени t = 0.

Пример. Экспериментально-аналитическая модель (строится на основе теории процесса, коэффициенты определяются экспериментально) – коэффициент пропорциональности к определяется на основании эксперимента (с телом неизменного состава и поверхности).

Температура окружающей среды постоянна. Скорость охлаждения тела в воздухе пропорциональна разности между температурой тела и температурой воздуха. Из решения ОДУ (dT (t)/ dt = - к (T _с - T), к – коэффициент пропорциональности):

ln (T – T _с) / (T ₀ – T _с) = - kt.

Например, при температуре окружающей среды T ₀ = 21 ⁰С, в течение часа температура тела снизилась с 31 до 29 С⁰. Тогда коэффициент пропорциональности к = ln (31 –21)/(29 –21) = 0,223. Зная к, можно определить время, за которое температура снизилась с 37 до 31 ⁰С:

T = 1/ к ln (37 –21)/(31 –21) = 2,1 часа.

Эффективные коэффициенты изменяются в зависимости от условия проведения опытов, поэтому экспериментально-аналитическая модель справедлива лишь в том интервале, в котором производился эксперимент.

Теоретический метод составления математических моделей

При теоретическом методе мaтемaтические модели составляются на основе применения фундаментальных законов природы к конкретной ситуации.

На первый план здесь выдвигается неформализованный ответ на вопрос, какой закон (или законы) применять в каждом конкретном случае и как это делать.

На основе фундаментальных законов природы и аналогий выделяется класс общих моделей с достаточно высоким уровнем абстракции. Такие модели строятся, могут самостоятельно изучаться, анализироваться, дополняться доказанными свойствами и утверждениями. Сведения, полученные при теоретическом рассмотрении, применимы ко всем конкретным соответствующим системам.

Это фундаментальные законы сохранения, которые являются общими для материального мира: массы, энергии, количества движения, импульса, заряда (законы Архимеда, Ньютона, Кулона и др.), постулат о непрерывном движении материи, принцип наименьшего действия (механические процессы протекают так, чтобы произведение затрачиваемой энергии на время ее затрачивания было минимальным).

Дата добавления: 2014-11-29