Однородные дифференциальные уравнения

Если в уравнении 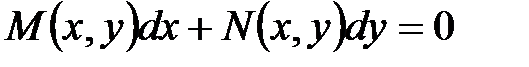(1)

функции М (x,y) и N (x,y) являются однородными функциями одной и той же степени, то уравнение (1) называется однородным.

Приведенное свойство однородных функций нулевого порядка используется при решении однородных дифференциальных уравнений, то есть имеет место равенство ƒ (x,y) = . Замечая, что в правой части стоит функция только одного аргумента 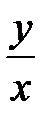, и обозначая её через 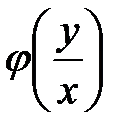, мы видим, что однородное уравнение всегда можно представить в виде (2)

При произвольно заданной непрерывной функции j переменные не разделяются. Но так как в правую часть переменные входят только в комбинации , то можно ожидать, что уравнение упростится, если ввести подстановку , откуда

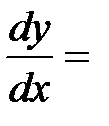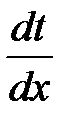y=tx, (3) тогда t+x . (4)

Подставим выражения (3) и (4) в уравнение (2) 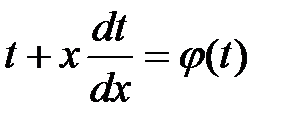, или .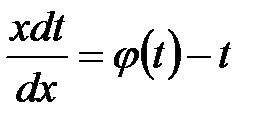

Таким образом, мы получили уравнение с разделяющимися переменным 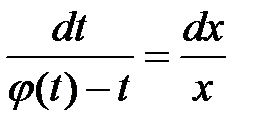(5)

В случае, когда 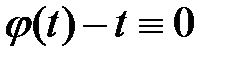(то есть ) уравнение (2) имеет вид , которое интегрируется с разделением переменных. Его общее решение .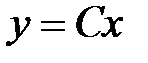

Алгоритм решения однородного дифференциального уравнения:

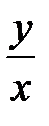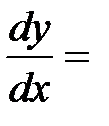1. Ввести новую функцию t = и подставить y = t x и t+x 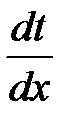в уравнение (2).

2. В новых переменных t и x получить уравнение с разделяющимися переменными и найти его общее решение.

3. В полученном решении произвести обратную замену переменных t = 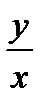и выписать решение исходного однородного уравнения.

Пример 2. Решить уравнение .

Решение. Разделим числитель и знаменатель правой части на x ²: . Введем замену , тогда наше уравнение перепишется следующим образом. После упрощения получаем 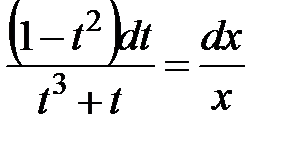. Проинтегрируем последнее уравнение . Разложим подынтегральное выражение на элементарные дроби .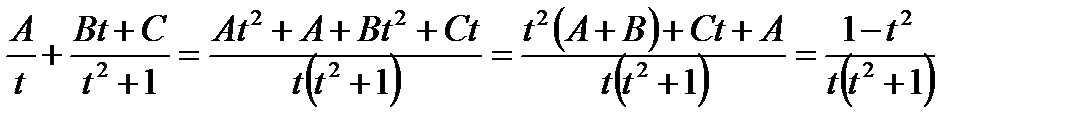

Þ получаем в итоге .

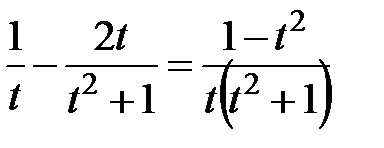Вычислим интеграл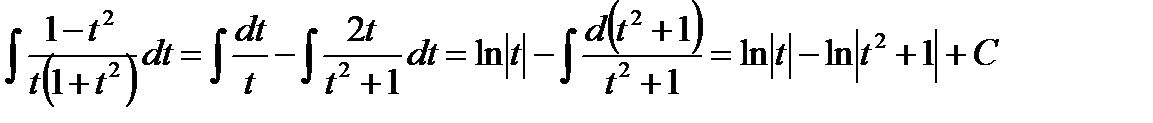

Окончательно получаем 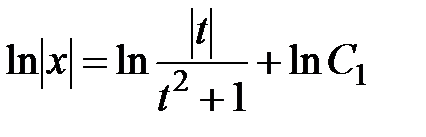, или .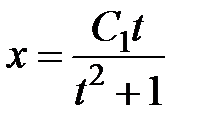

Делая обратную замену, получаем или .

Дата добавления: 2014-12-10