Немесе комбинаторика 4 страница

37. Санға цифрларының қосындысын қосу, шыққан санға өз цифрының қосындысын қосу амалын 7 рет қайталағанда 1004 шыққан болса алғаш қандай саннан басталған.

Нұсқау: Ең соңғы қосындыдан бастап ілгері жүру керек. Соңғы сан мен оның цифрларының қосындысының қосындысын 9-ға бөлгенде 5 қалдық қалу керек. 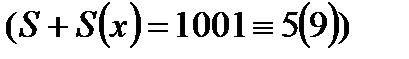немесе цифрларының қосындысы 23 не 14 болуы шарт екеніне көз жеткізу.

38. Тақтадағы 20, 21, 22, 23, 24, 25, 26, 27 сандарын бір жолға жазған. Келесі жолдарды көрші екі санның астына олардың көбейтіндісі келетіндей ең соңғы жолда бір ғана сан шыққанға дейін жалғастырады. Осы сан неше нольмен аяқталады?

Нұсқау: 2-жолдан бастап сандардың орнына сол санның аяқталатын нөлдерінің санын жазып кесте құр. Жауабы: 43 ноль.

39. Алғашқы екі цифрын және соңғы екі цифрын өшіргенде шығатын екі таңбалы сандардан 81 есе үлкен болатын 4 таңбалы санды тап.

Нұсқау: Бұл сан 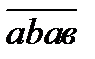түрінде болатынына көз жеткіз.

1.3.3. ЕКОЕ, ЕҮОБ, Евклид алгоритмі

Анықтама 1: Бірнеше сандардың бәрін бөлетін санды осы сандардың ортақ бөлгіші, ортақ бөлгіштердің ең үлкенін ең үлкен ортақ бөлгіш (ЕҮОБ) деп атайды.

ЕҮОБ-ті табу алгоритмі:

1. Берілген сандарды жай көбейткішке жіктейміз.

2. Барлық сандарға ортақ көбейткіштерді тауып көбейтіндісін аламыз.

Анықтама 2: ЕҮОБ-і 1-ге тең пар сандарды өзара жай сандар дейді. m; n сандарының ең үлкен ортақ бөлгішін ЕҮОБ(m;n) не (m;n) деп белгілейді.

Мысал: ЕҮОБ(60;25)-ті табайық.

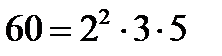
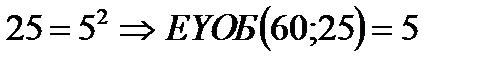
Жалпы жағдайда: 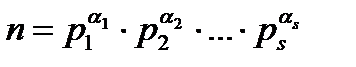, 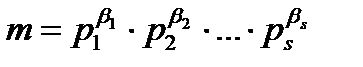cандары үшін

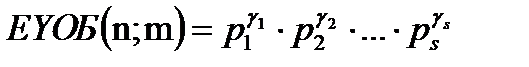
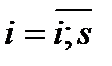
Анықтама 3: Бір неше сандарға бәріне де бөлінетін ең кіші санды сол сандардың ең кіші ортақ еселігі (ЕКОЕ) дейді.

ЕКОЕ ті табу алгоритмі :

1. Берілген сандарды жай көбейткішке жіктейді.

2. Алғашқы санның барлық көбейткіші мен келесі сандардың алғашқы санға кірмеген көбейткіштердің көбейтіндісін аламыз.

Мысалы: ЕКОЕ (12;30) – ды табайық

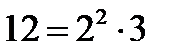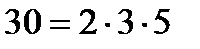, болғандықтан ЕКОЕ (12;30) =2·2·3·5 = 60 болады.

Жалпы жағдайда: 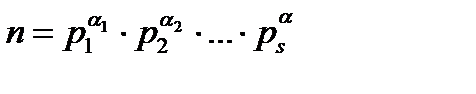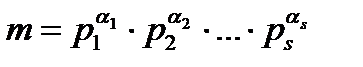болса 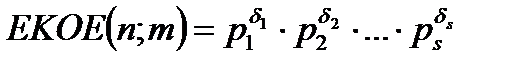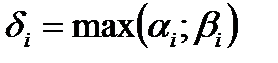, 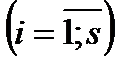болады.

ЕҮОБ-ті табудың Евклид алгоритмі:

Бұл алгоритм төменгі теоремаға негізделеді.

Теорема-1: а-және в-сандарының кез келген ортақ бөлгіші а – в санының бөлгіші болады.

Дәлелдеме: а; с, в;с болса а=mc, в=nc болады да а-в=mc-nc=(m-n)c

Теорема-2: а-санын в-ге бөлгенде бөлінді-q, қалдық r-ға тең немесе 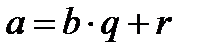, 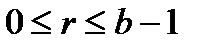болса ЕҮОБ (а; в)=ЕҮОБ (в; r) (1) болады

Дәлелдеме: (а; в)=d, (b;r)=h деп алып d=h дәлелдесек жеткілікті. 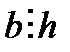, 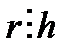немесе 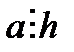болады. Бұдан . Сондай ақ 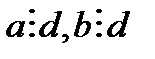, және r=a-bq болатындықтан . Немесе 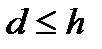. Бұдан 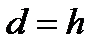болатыны дәлелденеді. Теорема-2 ні пайдаланып a, b сандарының ЕҮОБ-ін қалай табуға болатынын қарастырайық. Қалдықпен бөлуді тізбектей орындау арқылы шектеулі қадамнан соң 0 қалдық алатынымыз түсінікті. Себебі әр қалдық өзінің алдындағы қалдықтан кем және ден кем емес болатындықтан шектеусіз жалғасуы мүмкін емес. Немесе қалдық нольге тең болады, жәнеде теорема-2 бойынша 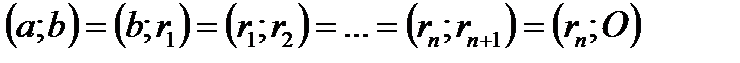ЕҮОБ- табуға арналған бұл тәсілді Евклид алгоритмі деп атайды.

Мысалы: 1381955 және 690713 сандарының ЕVОБ-ін тап.

(1381955; 690713) = (690713; 529) = (529; 368) = (368; 161) = (161; 46) = =(46; 23)=23

Біз жоғарыда төменгі теораманы дәлелдедік.

Теорема-3: Екі оң бүтін санға Евклид алгоритмін керектенгенде алғашқы нольге тең қалдықтың алдындағы қалдық бұл сандардың ЕVОБ-і болады.

Теорeма-4: Кез келген а; в- бүтін сандары үшін ax+ву=(а;в) болатындай х;у бүтін сандары табылады.

Дәлелдеме: Евклид алгоритмінің теңдіктердің соңынан екіншісінен 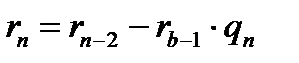мұндағы 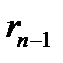-дің орнына соңынан 3-ші теңдіктен 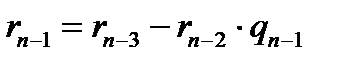-ді қойу амалын жалғастырып орындау арқылы ең соңында r 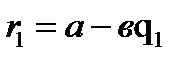-ді ауыстырып қойу нәтижесінде 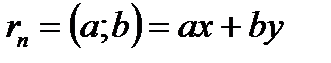теңдігіне жетеміз. Мұндағы х;у тер -лер тең бүтін сандарға қосу алу көбейту амалдарын керектену арқылы шығатындықтан бүтін сан болатыны түсінікті.

Жаттығу есептер:

1. Төменгі пар сандардың ЕҮОБ, ЕКОЕ-ін тап.

а) 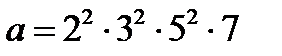және ,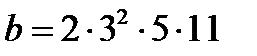

б) 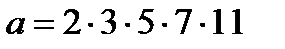және .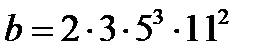

2. а) Қандай жағдайда ЕҮОБ(a, b) = a, қандай жағдайда ЕКОЕ(a, b) = a болады? Бірін бірі бөлетін сандардың ЕҮОБ- і ше?

б) 4, 15, 22, 77, 322 сандарынан өзара жай пар сандарды таңда. Өзара жай сандардың ЕКОЕ-і неге тең.

3. Евклид алгоритмін керекткеніп ЕҮОБ-ін тап.

a)2301 және 223200, б) 5959 және 6077, b) 5959 және 134333, г) 2n + 13 және n + 7, д) 12n + 1 және 30n + 2.

Екі санның қосындысы 221, ЕКОЕ- і 612 болса оларды тап.

4. Екі тақ санның айырмасы 8- ге тең болса ЕҮОБ-ін тап.

5. Екі тақ санның қосындысы 16-ға тең болса бұл сандар өзара жай сандар болатынын дәлелде.

6. 1, 2, 3, 4, 5, 6 цифрлары бір бір рет кірісіп жазылатын барлық 6 таңбалы сан нешеу? Осы сандардың ЕҮОБ-ін тап.

7. болса ЕҮОБ(n, n+1, n+2), ЕКОЕ(n, n+1, n+2) нің мүмкін мәндерін тап.

8. Тек 1 цифры арқылы жазылатын 100 және 60 таңбалы екі санның ЕҮОБ-ін тап. Бұл сандардың ЕКОЕ-і қандай сан болатынын анықта.

9. 324 см х141 см өлшемді тік төртбұрыштан қалған тік төртбұрыштың бір қабырғасы 141-ден кіші болғанынша қабырғасы 141 см квадраттар қиып алайық. Қалған тік төртбұрыштан оның кіші қабырғасына тең қабырғалы квадраттарды осылай қиып алу амалын жалғастырсақ ең соңында қиып алынатын қабырғасы бүтін сан болатын квадраттың қабырғасы неге тең болады?

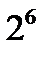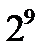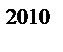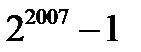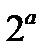10. Төменгі пар сандарының ЕҮОБ-ін тап: а) және , б) 2 -1 және в) және .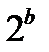

11. 2, 3, 4, 5, 6, сандарына бөлгенде әр қайсысында 1 қалдық қалады да 7 санына қалдықсыз бөлінетін барлық сандарды тап.

Нұсқау: Есептің шартын қанағаттандыратын сандар 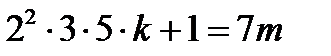теңдеуін қанағаттандыратынына көз жеткізіп, теңдеудің бүтін шешімдерін тап.

12. Екі оқушының біреуі көк қарындашпен оның басынан бастап 36см қашықтықта нүктелерді тізбектей белгілейді. Келесі оқушы лентаның басынан бастап ара қашықтықты 25см болатын нүктелерді қызыл қарындашпен белгілеген болса ара қашықтығы 1см ге тең қызыл және көк екі нүкте табыла ма? Қызыл және көк нүктелер қабаттасатын ара қашықтықты тап.

13. , (x, y) = 1 болса 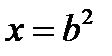, 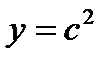болатындай b, c бүтін сандар табылатынын дәлелде.

14. 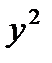= x(x + 1); 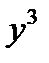= x(x + 1) теңдеулерінің барлық бүтін шешімдерін тап. Нұсқау. x, x + 1-дің біреуі 2- ге бөлінетіндіктен 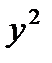4-ке, 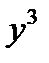8-ге бөлінетінін және 16-шы есептің нәтижесін пайдалан. Сондай-ақ теңдеуді x үшін квадрат теңдеу түріне келтіріп, түбірін зерттеп көруге де болатынын ескер.

15. 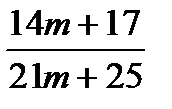бөлшегі қысқармайтынын дәлелде.

Нұсқау: Евклид алгоритмін пайдаланып (14m+17, 21m+25)-ті тап.

16. (a, a+1)=1, (a, a²+1)=1, (a, aⁿ +1)=1 болатынын дәлелде.

17. 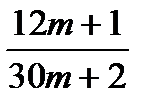; ; 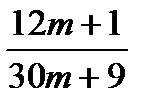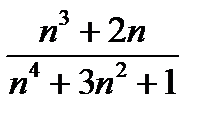бөлшектері қысқара ма?

18. (а; в) =1 болса (11а +2в,18а+5в) саны 1-мен 19-дың қай біріне тең болатынын дәлелде.

19. n-нің қандай мәнінде 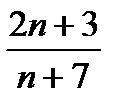; ; 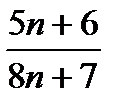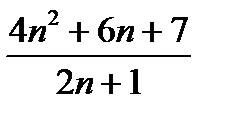бөлшектері қысқарады?

20. 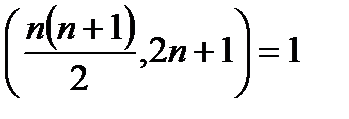болатынын дәлелде.

21. 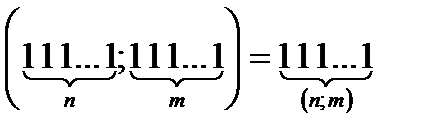болатынын дәлелде.

22. 25x - 36y = 1 теңдеуінің бүтін шешімін тап.

23. 13x + 16y = 300 теңдеуінің натурал шешімін тап.

24. 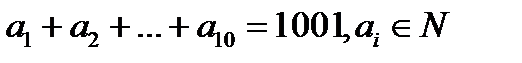болса EVОБ - ның алуға болатын ең үлкен мәнін тап. (Жауабы: 91)

25. 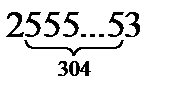және 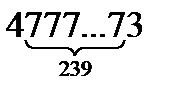сандарының EVOБ–ін тап.

Нұсқау: 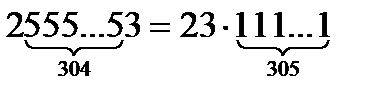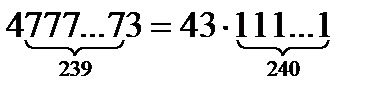болатынына көз жеткіз. (305; 240) =5 болатынын ескер.

26. Егер 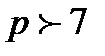жай сан болса 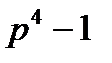саны 240-қа бөлінетінін дәлелде.

Нұсқау: 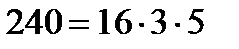және 3; 5; 16 сандары пар парымен өзара жай болатындықтан 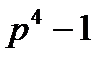саны 16-ға, 3-ке, 5-ке бөлінетінін дәлелде.

27. 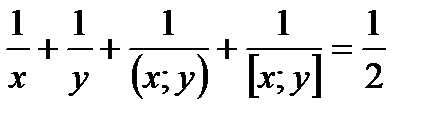теңдеуінің шешімі болатын натурал пар сандарды тап.

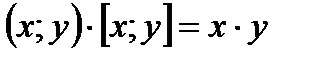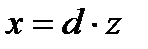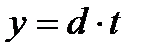
Нұсқау: (x; у)= d десек , 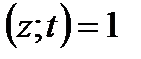және 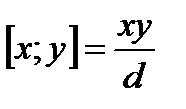болатынын пайдаланып теңдеуді түрлендірсек теңдеу 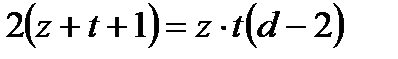немесе 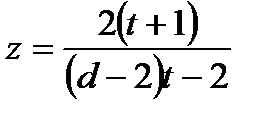түріне келеді де 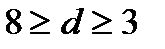болуы шарт және бүтін шешімі болу үшін 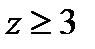болу керектігін айқындап d-нің барлық мүмкін мәндерін қарастыра отырып теңдеудің шешімін табу керек.

1.4. Диофант теңдеу шешу тәсілдері

1.4.1. Сызықтық Диофант теңдеу шешу

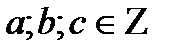және a, b қатар нольге тең болмайтын (кемінде біреуі нольден өзгеше) жағдайда 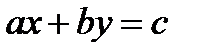(1) теңдеуінің бүтін шешімін табу есебі сызықтық Диофант теңдеу шешу деп аталады.

Ең әуелі Сызықтық Диофант теңдеудің (кемінде бір) бүтін шешімі болуының қажетті шартын анықтайық. Немесе (1) теңдеуінің бүтін шешімі болу үшін қандай шарт орындалуы қажет екеніне тоқталайық.

a, b сандарының ең үлкен ортақ бөлгішін d деп белгілейік. 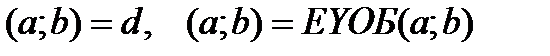. Бұдан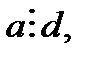 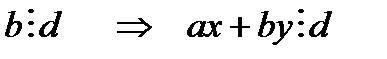болатындықтан 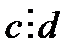болуы шарт. Олай болса с -саны d -ге бөлінбесе (еселік болмаса) теңдеуінің бүтін шешімі болуы мүмкін емес.

Ал 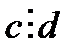болса немесе 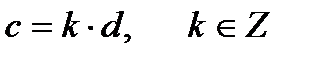шарты орындалса, онда 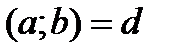жағдайда 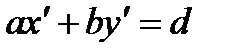болатын (x'; y') пар бүтін сандар табылатынына Евклид алгоритімін пайдаланып көз жеткізу қиын емес. Мәселен d -санын Евклид алгоритімін пайдаланып табу жолы:

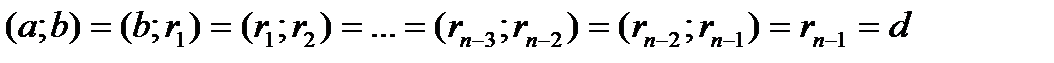
Яғни ең соңғы 0 қалдық шығатын бөлгішке тең сан а;b сандарының ЕҮОБ- і болады.

Мұны 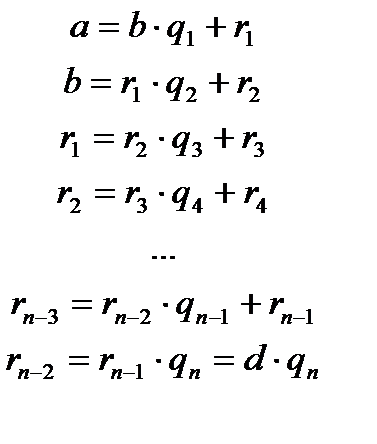(2)

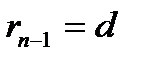түрінде жазып, (2)-ден аяғынан екінші теңдіктен бастап қалдықтарды тауып бір-біріне тізбектей ауыстырып қою арқылы:

=

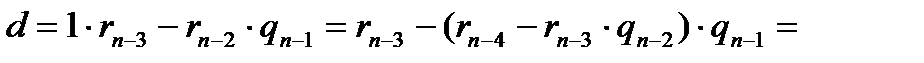
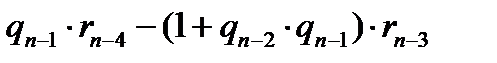
ең соңында 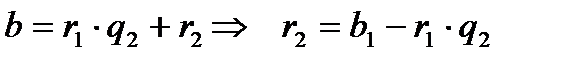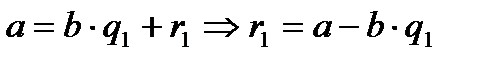теңдіктерінен а; b арқылы өрнектеліп а; b- нің коэффициенттері бүтін сандар мен -лерге көбейту, қосу амалдарын керектенген өрнек болатындықтан мәні бүтін сандар шығады да оларды х’; у’ деп белгілесек: 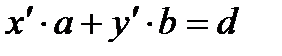(3) болады. 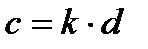деп алғандықтан (3) теңдіктің екі жағын k -мен көбейтсек 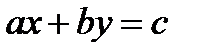теңдеуінің бүтін шешімі болатыны дәлелденді.

Қорытынды: а) Егер c саны 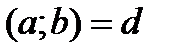-ге бөлінбесе 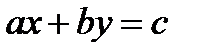теңдеуінің бүтін шешімі болмайды.

б) Егер c саны 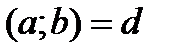- ге бөлінетін болса (1) теңдеуінің шексіз көп бүтін шешімі болады.

Енді бүтін шешімді табу жолын қарастырайық.

Ол үшін мысал ретінде 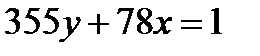теңдеуін алып көрейік. Алдымен ЕҮОБ (355; 78)- ді Евклид алгоритмі бойынша табайық.

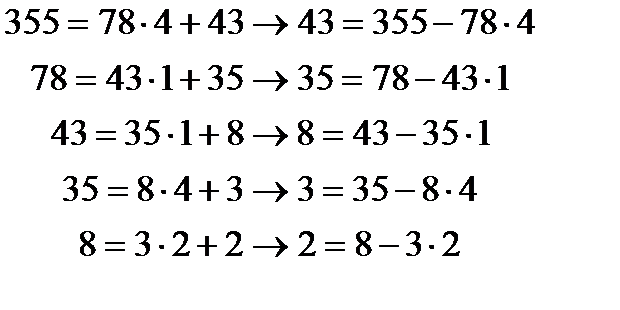(3)

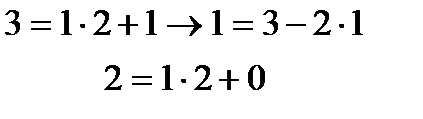
0 қалдық кезіндегі бөлгіш 1-ге тең немесе ЕҮОБ(355; 78)=1 болады да (3) теңдіктерді соңынан бастап бірін біріне ауыстырып қойып есептесек:

=

=

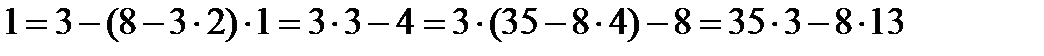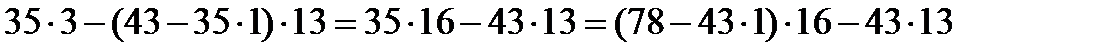
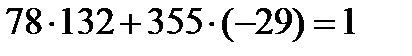= Немесе болды. Осылай сызықтық Диофант теңдеудің қандай бір шешімін Евклид алгоритмін пайдаланып табуға болатынына көз жеткіздік.

Енді негізгі шешімін қалай табуға болатынын қарастырайық. Әуелі жазықтық нүктелеріне 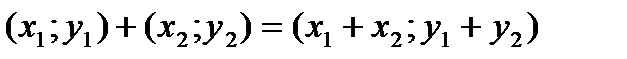(4) заңдылығы бойынша қосу амалын енгізейік. Бұл амал нәтижесінде «бүтін нүктелердің қосындысы бүтін нүктелер болады». Сондай ақ ax + by = n теңдеуінің графигін 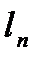, ax + by = m теңдеуінің графигін деп белгілесек, бұлар өзара параллель түзулер болады да түзуінің нүктелеріне түзуінің нүктелерін (4) заңдылығы бойынша қоссaқ 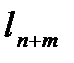түзуінің нүктелері шығады. Бұдан (1) теңдеуінің негізгі шешімін табуға өте маңызды төменгі қортынды шығарып аламыз:

ax + by = 0 (5) теңдеуінің шешімі болатын түзуінің барлық нүктелеріне ax + by = с теңдеуінің шешімдерінің жиыны болатын түзуінің қандай бір нүктесін (4) заңдылығы бойынша қоссақ түзуінің барлық нүктесін шығарып аламыз.

Сондай ақ түзуінің кез келген нүктесін басы координаталар басында, ұшы сол нүктеде болатын вектордың координатасы деп көруге болатындықтан осы заңдылық бойыша (5) теңдеуінің әр бір бүтін шешіміне бүтін координаталы векторлар сәйкес келетіні түсінікті. Сондай ақ (1) теңдеуінің қандай бір бүтін шешімін 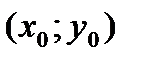деп белгілесек, аталмыш заңдылық боынша оған 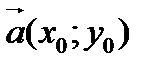векторы сәйкес келеді.

Егер (5) теңдеуінің кез келген бүтін шешімі арқылы анықталатын векторды 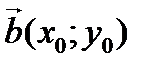деп алсақ, барлық 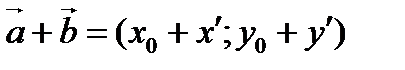(*) векторларларының координата-ларының жиыны (1) теңдеудің барлық шешiмдерін беретініне көз жеткізу қиын емес. Сондықтан алдымен ax+by = 0 (5) теңдеуінің шешімін табамыз. ЕҮОБ (а;b)=d деп алсақ 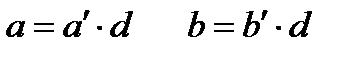болатын 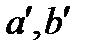бүтін сандары табылады. Және де 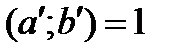болады да 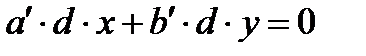бұдан 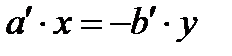болғандықтан 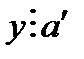немесе 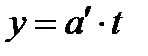болады.

Бұдан 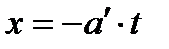немесе ax + by = 0 теңдеуінің негізгі шешімі: формуласымен анықталады екен. Олай болса жоғрыдағы қортындылар мен (*) векторлық теңдігінен:

ax + by = с теңдеуінің c- саны d=(а;b)-ге бөлінетін кезде 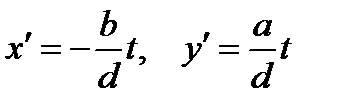формуласы бойынша анықталатын шексіз көп шешімі болатыны айқын болды. Мұнда 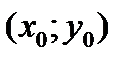пары ax + by = с теңдеудің қандай бір шешімі.

Жаттығу есептері:

1. Теңдеулердің жалпы шешімдерін тап.

a) 53x + 74y = 1, b) 310x + 122y = 4,

c) 2006x + 2007y = 2008, d) 1003x + 1005y = 2009

e) 127x – 52y = 1

2. a) 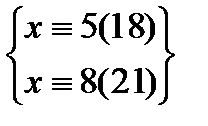b) 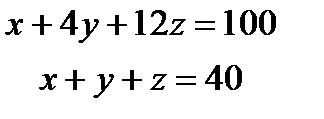системасын шеш

3. Ауладағы үйрек, мысық, тасбақалардың барлық саны 13, аяқтарының саны 42. (тасбақада 6 аяқ бар деп ал) Үйрек, мысық, тасбақаның әр қайсысы нешеу?

4. 1, 10 және 50 теңгелік 100 монетадан 500 тенге төлеуге болама?

5. 2-лік және 5-тік тиындар арқылы 48 тиынды төлеудің барлық мүмкін жағдайларын көрсет. Осы құнды 5-тік жіне 10-дық тиындар арқылы дәл қайтара аласыз ба?

6. 2, 5, 8,..., 323 және 7, 12, 17,..., 512 екі арифметикалық прогрессияның ортақ мүшелері болатын сандарды тап.

Дата добавления: 2014-12-16