
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Предел функции в точке
Определение: Последовательностью называется функция натурального аргумента  ,
,  ,
,  ,…,
,…, 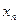 ,…,
,…, 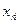 ,…. Причем если
,…. Причем если  , то
, то 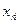 следует за
следует за 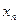 , независимо от того, больше он его или меньше.
, независимо от того, больше он его или меньше.
Последовательность чисел называется сходящейся к числу  , если для любого положительного, сколь угодно малого числа
, если для любого положительного, сколь угодно малого числа  (эпсилон) найдется такой номер
(эпсилон) найдется такой номер  , что для всех номеров
, что для всех номеров  будет выполняться неравенство
будет выполняться неравенство  . Пишут
. Пишут  .
.
Геометрический смысл предела последовательности состоит в том, что за пределами 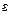 – окрестности точки
– окрестности точки 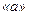 находится лишь конечное число членов последовательности
находится лишь конечное число членов последовательности  , а внутри этой окрестности находится бесконечное множество членов последовательности и при
, а внутри этой окрестности находится бесконечное множество членов последовательности и при  число
число 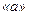 будет сгустком точек, соответствующих членам последовательности.
будет сгустком точек, соответствующих членам последовательности.
Определение: Число  называется пределом функции
называется пределом функции  в точке
в точке  , если для любого
, если для любого  сколь угодно малого положительного числа
сколь угодно малого положительного числа  найдется
найдется  положительное число
положительное число 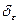 (дельта), что для всех
(дельта), что для всех  , удовлетворяющих неравенству
, удовлетворяющих неравенству  , выполнится неравенство
, выполнится неравенство  .
.
Пишут  .
.
Теоремы о пределах функций: если существует  и
и  , то
, то
1)  ;
;
2)  ;
;
3)  ;
;
4)  при
при 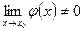 .
.
При вычислении пределов используются два замечательных предела:
1)  (первый замечательный предел);
(первый замечательный предел);
2)  (второй замечательный предел).
(второй замечательный предел).
Определение: Функция  называется бесконечно малой в точке
называется бесконечно малой в точке  , если
, если  .
.
Определение: Функция  называется бесконечно большой в точке
называется бесконечно большой в точке  , если
, если  .
.
Теорема: Если  – бесконечно большая функция, то
– бесконечно большая функция, то  – бесконечно малая функция. Если
– бесконечно малая функция. Если  – бесконечно малая и
– бесконечно малая и  – бесконечно малая функция в точке
– бесконечно малая функция в точке  и
и 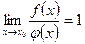 , то
, то  и
и  эквивалентны. Пишут
эквивалентны. Пишут  ~
~  .
.
v Найти пределы функций, не используя правило Лопиталя.
а) 
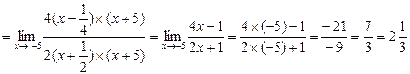

| 
|
б)  /выносим в числителе и знаменателе старшие степени переменной, затем производим возможные сокращения/
/выносим в числителе и знаменателе старшие степени переменной, затем производим возможные сокращения/

 т.к. при
т.к. при 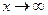 значения дробей
значения дробей  стремится к 0.
стремится к 0.
в)  = /умножим числитель и знаменатель на выражение
= /умножим числитель и знаменатель на выражение 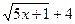 ; знаменатель разложим на множители/
; знаменатель разложим на множители/ 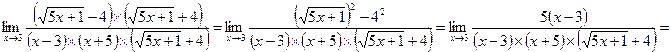

г) 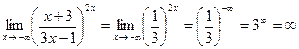
д) 
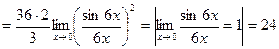 ;
;
е) 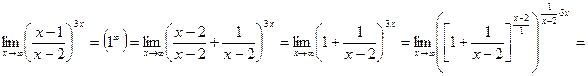
=  .
.
Определение: Функция  называется непрерывной в точке
называется непрерывной в точке  , если существует предел функции в точке
, если существует предел функции в точке  , равный значению функции в точке
, равный значению функции в точке  , т. е.
, т. е.  .
.
Иными словами, функция непрерывна в точке  , если выполняются равенства:
, если выполняются равенства:
 (*)
(*)
Односторонние пределы функции в точке  равны значению функции в точке
равны значению функции в точке  .
.
Определение: Точка  называется точкой разрыва первого рода, если существуют конечные, но неравные односторонние пределы функции в точке
называется точкой разрыва первого рода, если существуют конечные, но неравные односторонние пределы функции в точке  . Разность между правым и левым пределами называется скачком.
. Разность между правым и левым пределами называется скачком.
Определение: Точка  называется точкой разрыва второго рода, если хотя бы один из односторонних пределов равен
называется точкой разрыва второго рода, если хотя бы один из односторонних пределов равен  или не существует.
или не существует.
Определение: Точка  называется точкой разрыва устранимого, если существует предел функции в этой точке, не равный значению функции в точке
называется точкой разрыва устранимого, если существует предел функции в этой точке, не равный значению функции в точке  .
.
v Исследовать функцию на непрерывность и построить график:
 .
.
Решение: Функция  является непрерывной на каждом из промежутков, поэтому подозрительными на разрыв являются точки
является непрерывной на каждом из промежутков, поэтому подозрительными на разрыв являются точки 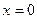 и
и  . Исследуем каждую точку.
. Исследуем каждую точку.
1) 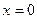 . Найдем левосторонний и правосторонний пределы функции
. Найдем левосторонний и правосторонний пределы функции  при
при 

 ,
,
значение функции в точке 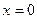 равно:
равно: 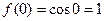 . Следовательно, в точке
. Следовательно, в точке 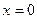 функция является непрерывной, так как
функция является непрерывной, так как 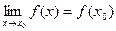 .
.
2) 

 .
.
Так как односторонние пределы конечны, но не равны, то точка  является точкой разрыва первого рода.
является точкой разрыва первого рода.
Скачок равен 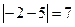 .
.


Производная функции, её приложение
Определение: Пусть функция  задана на некотором множестве
задана на некотором множестве  . Зафиксируем значение аргумента
. Зафиксируем значение аргумента  и придадим ему приращение
и придадим ему приращение  , не выводящее значение аргумента за пределы множества
, не выводящее значение аргумента за пределы множества  , т. е.
, т. е.  . Тогда соответствующее приращение
. Тогда соответствующее приращение  получит и сама функция, которое равно разности нового и старого значений функции:
получит и сама функция, которое равно разности нового и старого значений функции:  . Если существует конечный предел отношения приращения функции к приращению аргумента при
. Если существует конечный предел отношения приращения функции к приращению аргумента при  , то он называется производной функции в точке
, то он называется производной функции в точке  . Пишут
. Пишут  , или
, или  . (6)
. (6)
Если  существует во всех точках множества
существует во всех точках множества  , то
, то  является функцией от
является функцией от  .
.
Таблица производных основных элементарных функций
Если  является дифференцируемой, то выполняются равенства:
является дифференцируемой, то выполняются равенства:
1.  где
где 
2.  где
где 
3. 
4. 
5. 
6. 
7. 
8. 
9. 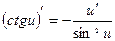
10. 
11. 
12. 
13. 
14. 
15. 
16. 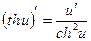
17.  .
.
Основные правила дифференцирования:
1. 
2. 
3. 
4. 
5. 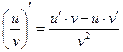
6. 
7. Если  и
и  , т. е.
, т. е.  , то
, то  , где и и φ – дифференцируемы.
, где и и φ – дифференцируемы.
8. Если для функции 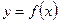 существует обратная дифференцируемая функция
существует обратная дифференцируемая функция  , то
, то  .
.
v Найти производные функций
а)  ;
;
б) 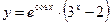 ;
;
в)  .
.
Решение:
1)  .
.
Преобразуем функцию 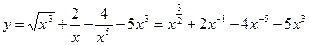

б) 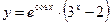
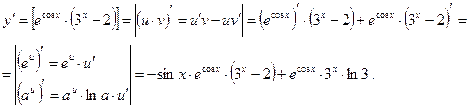
в) 

Определение: Производной второго порядка функции 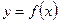 называется производная от первой производной, т. е.
называется производная от первой производной, т. е. 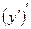 . Обозначают
. Обозначают  .
.
Определение: Производной n -го порядка функции 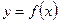 называют производную от производной (n – 1)-го порядка данной функции. Обозначают
называют производную от производной (n – 1)-го порядка данной функции. Обозначают 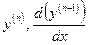 .
.
|
|
Дата добавления: 2014-12-16; Просмотров: 1276; Нарушение авторских прав?; Мы поможем в написании вашей работы!