Методы одномерной оптимизации

Эти методы строятся в предположении унимодальности функции F(x) на заданном интервале [a, b]. К функции не предъявляются требования непрерывности или дифференцируемости, предполагается лишь, что для любого x Î [a, b] значение F(x) может быть вычислено.

Методы одномерного поиска можно разделить на методы последовательного поиска (методы сокращения интервалов: дихотомии, золотого сечения и Фибоначчи) и методы, использующие аппроксимацию функции (методы квадратичной и кубической интерполяции и др.)

ü Методы последовательного поиска (методы сокращения интервалов, методы исключения интервалов)

Методы этой группы нацелены на построение такой стратегии поиска x*, при которой любая пара вычислений F(x) позволяет сузить область поиска (или интервал неопределенности). Вычисляя F(x) в точках x₁ и x₂ таких, что a < x₁ < x₂ < b, можно локализовать интервал неопределенности путем анализа полученных значений функции:

если F(x₁) < F(x₂), то x* Î [a, x₂];

если F(x₁) = F(x₂), то x* Î [x₁, x₂];

если F(x₁) > F(x₂), то x* Î [x₁, b];

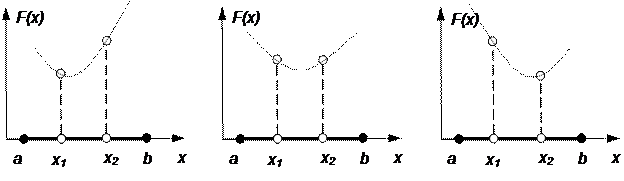Основное различие между методами последовательного поиска состоит в стратегиях выбора значений x₁ и x₂.

· Метод дихотомии (половинного деления) – один из самых простых методов последовательного поиска.

Метод половинного деления (метод дихотомии) проиллюстрирован ниже.

· Метод золотого сечения предполагает такое сокращение интервала на каждом шаге, что отношение целого к большей части было равно отношению большей части к меньшей. Это отношение, равное 1.618, и называют «золотым сечением». (1: 0,618 = 1,618; 0.618: 0,382 = 1,618)

Координаты точек x_1,k и x_2,k определяются следующим образом:

x_1,k = a_k + 0.382×(b_k – a_k); x_2,k = b_k – 0.382×(b_k – a_k).

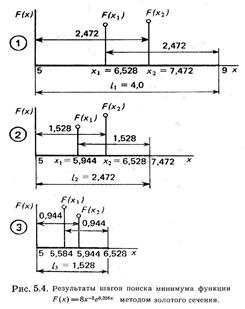
Значение коэффициента К (0,382) подобрано так, что в полученном отрезке меньшей длины одна из промежуточных точек совпадет с промежуточной точкой от предыдущего шага. Это позволяет сократить число вычислений целевой функции на всех шагах (кроме первого) в 2 раза.

Таким образом, требуется не более N шагов и N+1 вычисление целевой функции, где N можно рассчитать, используя соотношение (b–a)/ε = (1–a)N при заданной погрешности ε определения экстремума.

САПР-1986, кн. 9:	САПР-1986, кн. 8:

· Метод чисел Фибоначчи

Стратегия поиска связана с использованием чисел Фибоначчи, которые можно получить из рекуррентного соотношения R_k = R_k-1 + R_k-2, k = 2, 3, …, R₀ = R₁ = 1. В отличие от метода золотого сечения, здесь коэффициент сокращения интервала изменяется от итерации к итерации, хотя он также близок к значению 0.382.

Норенков-2000: Согласно методу чисел Фибоначчи, используют числа Фибоначчи R_i, последовательность которых образуется по правилу R_i+2 = R_i+1 + R_i при R₀ = R₁ = 1, т.е. ряд чисел Фибоначчи имеет вид 1, 1, 2, 3, 5, 8, 13, 21, 34,.... Метод аналогичен методу золотого сечения с тем отличием, что коэффициент K равен отношению R_i-2 /R_i, начальное значение i определяется из условия, что R_i должно быть наименьшим числом Фибоначчи, превышающим величину (b–a)/ε, где ε — заданная допустимая погрешность определения экстремума. Так, если (b–a)/ε = 100, то начальное значение i = 12, поскольку R₁₂ = 144, и K = 55/144 = 0,3819, на следующем шаге будет K = 34/89 = 0,3820 и т.д.

Основной недостаток метода – необходимость задания числа шагов. Основное преимущество – быстрое сужение интервала неопределенности: при числе шагов n = 14 интервал неопределенности примерно в 5 раз меньше, чем получаемый по методу половинного деления. В то же время по сравнению с методом золотого сечения метод Фибоначчи позволяет получить интервал только на 17% меньше, и при большом числе шагов оба эти метода практически идентичны.

ü Методы полиномиальной аппроксимации

Общая идея методов, использующих аппроксимацию функции, основана на приближении функции гладким полиномом и использовании этого полинома для оценки координаты минимума.

· Метод квадратичной интерполяции – один из популярных методов этой группы.

Метод заключается в замене нелинейной функции F(x) квадратичной параболой F₂(x), построенной по трем точкам, принадлежащим F(x), так, чтобы значения аппроксимирующей функции F₂(x) совпали со значениями F(x) в этих трех точках. Минимум квадратичной функции находится с использованием аналитического условия оптимальности: df/dx = 0.

На первом этапе в качестве исходных трех точек используются

x₁ = a, x₂ = (a + b)/2, x₃ = b.

В этих точках вычисляется f(x) и по полученным точкам f(x₁), f(x₂), f(x₃) строится парабола

f₂ = C₂ x² + C₁ x + C₀,

коэффициенты которой находятся из решения соответствующей системы уравнений:

f₂(x₁) = f(x₁), f₂(x₂) = f(x₂), f₂(x₃) = f(x₃)

Значения коэффициентов:

C₀ = f(x₁),

C₁ = [f(x₂) – f(x₁)] / (x₂ – x₁),

C₂ = 1 / (x₃ – x₂)× {[ f(x₃) – f(x₁)] / (x₃ – x₁) – [f(x₂) – f(x₁)] / (x₂ – x₁)}

Условие оптимальности приводит к уравнению x₄ = – C₁ / 2C₂, где х₄ – точка минимума параболы f₂(x).

Далее выбирается новый отрезок, внутри которого находится точка х₄, и c использованием х₃, х₄ строится новая парабола, по которой уточняется положение минимума f(x), и т. д. до тех пор, пока величина отрезка, внутри которого находится оптимум, не станет меньше заданной погрешности e. Таким образом, метод имеет итерационный характер.

К достоинствам метода относится высокая скорость сходимости, хотя метод может не всегда сходиться.

Например, на рис. ниже показана ситуация (для случая максимизации функции), когда метод параболической аппроксимации сходится к решению уже на третьем этапе: парабола 3, построенная по точкам х₃, х₄, х₅, практически совпадает с исходной функцией 1.

Пример. Найти максимум функции f(x) = sin (x + 1) на интервале [-1; 2], точность e = 0,01.

Решение. Для построения аппроксимирующей параболы находим точки

x₁ = a, x₂ = (a + b)/2, x₃ = b.

Система уравнений для нахождения коэффициентов параболы примет вид:

Решение системы можно найти любым из известных способов, например, по формулам Крамера. На первом шаге получаем = 0,5571, f( ) = 0.9999. По этой точке, а также по второй и третьей исходным точкам, лежащим по обе стороны от точки максимума параболы, аналогично строится вторая парабола.

п	x1	x2	x3	f(х1)	f(x2)	f(x3)	C2	C1	C0
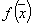
1	-1	0.5	2	0	0.9975	0.1411	-0.412	0.459	0.871	0.5571	0.9999
2	0.5	0.5571	2	0.9975	0.9999	0.1411	-0.4249	0.4914	0.858	0.5782	1
3	0.5571	0.5782	2	0.9999	1	0,1411	-0,4208	0.4809	0.8626	0.5714	1
4	0,5571	0,5714	0,5782	0,9999	1	1	-0,5	0,5708	0,8371	0,5708	1

Уже на третьем шаге разница между двумя точками максимума менее заданной погрешности, поэтому поиск можно заканчивать (четвертый шаг приведен для наглядности вычислений). Поэтому х*» 0,5708, и f*» f (0,5708) = 1.

Кроме описанных методов, существует и ряд других, например, метод Пауэлла, предусматривающий последовательное применение квадратичной аппроксимации, метод Давидона, использующий кубическую аппроксимацию, и др. Примеры программной реализации различных методов приведены в литературе, например, в книге Б. Банди «Методы оптимизации».

Заметим, что универсального метода, наилучшего для любых задач, пока не создано. Поэтому в современных математических пакетах возможна автоматическая смена метода в процессе решения задачи, как например в Matlab – переход от метода золотого сечения (golden) к методу квадратичной аппроксимации (parabolic):

Дата добавления: 2014-12-16