Особенности оптимизационных задач

Пусть в проектируемом объекте имеется n управляемых параметров, образующих вектор X = (x₁, x₂, …, x_n). Обозначим целевую функцию F(X), а область ее определения – XO. Вектор X определяет координаты точки в области определения XO.

Если элементы вектора X принимают только дискретные значения, то XO является дискретным множеством точек и задача оптимизации относится к области дискретного программирования (в частном случае – целочисленного программирования). Большинство задач параметрической оптимизации технических объектов формулируется в терминах непрерывных параметров.

Если экстремум целевой функции ищется в неограниченной области XO, то его называют безусловным, а методы поиска – методами безусловной оптимизации. Если же на значения управляемых параметров наложены ограничения, которые сужают область XO, то экстремум называют условным, а применяемые методы – методами условной оптимизации. Однако в большинстве практически важных случаев задачу удается свести к задаче безусловной оптимизации.

e-окрестностью точки X_p называют множество S_e (X) точек (векторов), которые находятся от точки X_p на расстоянии, не превышающем заданного числа e > 0:

S_e (X) = { X | ‖ X – X_p ‖ £ e},

где ‖ X – X_p ‖ - норма вектора, понимаемая как расстояние между точками X и X_p.

Максимумом или минимумом функции F(X) называют ее значение F(X*), если для любой точки X Î S_e(X*) при достаточно малом e > 0 (за исключением самой точки X*) выполняется неравенство F(X) – F(X*) < 0 или F(X) – F(X*) > 0 соответственно. Точку X* называют точкой локального экстремума.

Глобальным экстремумом называют точку, в которой целевая функция имеет наибольшее (или наименьшее) значение среди всех локальных экстремумов области определения.

Функцию F(X) называют одноэкстремальной (унимодальной), если она имеет один экстремум, и многоэкстремальной, если она имеет более одного экстремума (см. рис.).

При анализе различных методов поиска экстремума полезны геометрические представления.

Геометрически система значений двух переменных (x, y) изображается точкой на плоскости, а функция двух переменных z = F(x, y) – некоторой поверхностью в пространстве; система значений трех переменных (x, y, z) изображается точкой в пространстве. Система значений четырех и более переменных не имеет геометрического изображения. Однако для упрощения записей и рассуждений, систему значений любого числа n переменных (х₁,..., х_п) называют точкой n-мерного пространства M(х₁,..., х_п), а функцию u, зависящую от n переменных, называют функцией точки n -мерного пространства u = f(х₁,..., х_п).

Поверхность отклика (Response Surfase) функции двух переменных F (X) = F(x₁, x₂) удобно представлять совокупностью линий равных уровней (см. рис.). Эти линии получаются при пересечении поверхности отклика F(X) плоскостями, параллельными плоскости координат (x₁, x₂).

При наличии ограничений типа равенств или неравенств характер их поведения также удобно изображать на той же плоскости, имея в виду, что каждое из уравнений функций-ограничений определяет в n -мерном пространстве ( n – 1)- мерную поверхность. На плоскости (x₁, x₂) ограничение представляется некоторой линией. Штриховкой отмечается допустимая область поиска.

Линии равных уровней поверхности отклика и линии ограничений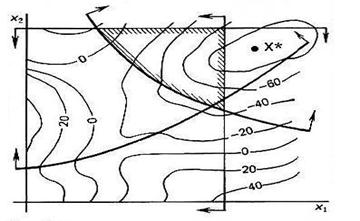
Геометрическая модель оптимизации с ограничениями [Дитрих-1981]: Целевая функция z = wxx + wyy ® MIN. Ограничения: f1 = a1xx + a1yy ≥ r1, f2 = a2xx + a2yy ≥ r2, f3 = a3xx + a3yy ≥ r3. Уравнение целевой функции соответствует плоскости, проходящей через начало координат О. Ограничивающими функциями являются величины ri, которые нельзя переступать, а их графические отображения представляют собой следы пересечения многогранника с плоскостью xy. …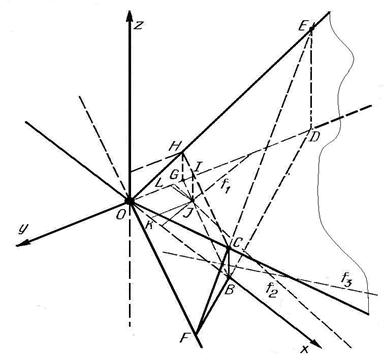
Графическая модель оптимизации с ограничениями

Замечание: При трех и более проектных параметрах поверхности, задаваемые целевой функцией, называются гиперповерхностями и не поддаются изображению обычными средствами.

Геометрические представления удобно использовать для выражения характерных особенностей функций, например таких, как многоэкстремальность, овражность, наличие седловых точек.

Особенности поведения поверхностей отклика целевых функций
Многоэкстремальность
Овражный характер
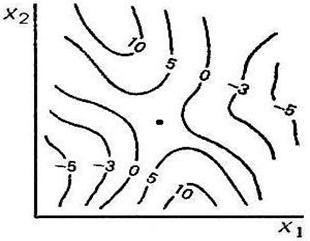
Седловая точка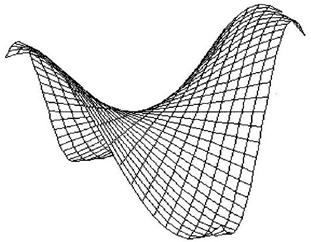

Литература

1. Конюховский П.В. Математические методы исследования операций в экономике. – СПб.: Изд-во СПбГУ, 2008.

2. Таха Х. Введение в исследование операций. - М.: Мир, 1985.

3. Банди Б. Основы линейного программирования, 1989.

4. Норенков И.П. Основы автоматизированного проектирования, 2000.

5. Системы автоматизированного проектирования: Учебн. пособие для ВУЗов: В 9 кн. / Под ред. И.П. Норенкова. - М.: Высш. шк., 1986.

Дата добавления: 2014-12-16