Нормальный закон распределения

Гипергеометрическое распределение

Пусть имеется множество N элементов, из которых М элементов обладают некоторым признаком A. Извлекается случайным образом без возвращения n элементов. Требуется найти вероятность того, что из них m элементов обладают признаком A. Искомая вероятность (зависящая от N, M, n, m) определяется по формуле:

Если по формуле вычислить вероятности для всех возможных значений m, то полученный ряд распределения называется гипергеометрическим законом распределения

M				...	n
P(X=m)				...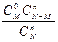

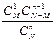
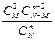
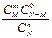
Математическое ожидание и дисперсия случайной величины m, распределенной по гипергеометрическому закону, определяются формулами:

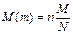
Если плотность распределения (дифференциальная функция) непрерывной случайной величины определяется выражением:

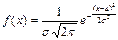
то говорят, что Х имеет нормальное распределение с параметрами а и 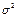. Вероятностный смысл параметров: , а 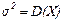. Обозначение:

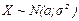
Для расчета вероятности попадания нормально распределенной случайной величины Х в промежуток от до используется формула:

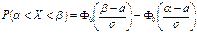
(интеграл Лапласа)

Формула иногда в литературе называется интегральной теоремой Лапласа.

Функция обладает свойствами:

3 ) 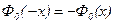(см. таблицу приложения 2).

Функция табулирована. В частности для симметричного относительно а промежутка 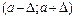имеем:

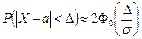
Формула применима и к частоте m, поскольку ее закон распределения при достаточно большом числе испытаний практически совпадает с нормальным. Применительно к случайной величине m, с учетом ее числовых характеристик

M(m) = np и

формула примет вид:

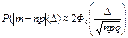
Формула может быть применена и к относительной частоте 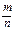с числовыми характеристиками и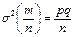

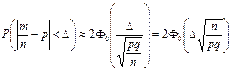
С вероятностью, очень близкой к единице (равной 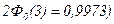нормально распределенная случайная величина Х удовлетворяет неравенству:

В этом состоит правило трех сигм: если случайная величина распределена по нормальному закону, то ее отклонение от математического ожидания практически не превышает .

Локальная теорема Муавра-Лапласа. При р или p 1 и достаточно большом n биноминальное распределение близко к нормальному закону (причем их математические ожидания и дисперсии совпадают), т.е. имеет место равенство:

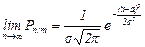, где ,

Тогда:

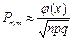
для достаточно больших n (здесь 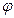(х) - плотность вероятностей стандартной нормальной случайной величины 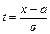и ).

Дата добавления: 2014-12-16