
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Нестандартизированные задачи
|
|
|
|
В результате варьирования условия можно получить нестандартизированную задачу.
Стандартизированные или определенные – задачи, содержащие в условии необходимое и достаточное количество данных для получения единственно возможного ответа.
К нестандартизированным можно отнести неопределённые, переопределённые, нереальные или противоречивые, вариативные, провоцирующие задачи, задачи с несформированным требованием. Необходимость использования таких задач, коренным образом изменяющих мыслительные процессы решающего, превращая их в более сложные, более содержательные, доказывается Д.Пойа, Ю.М. Колягиным, П.М. Эрдниевым, В.А. Крутецким, Н.В. Метельским и другими.
Вариативные задачи и задачи с несформированным требованием уже были рассмотрены. Дадим характеристику неопределённым, переопределённым, нереальным или противоречивым, провоцирующим задачам.
Неопределённые задачи – задачи с неполным условием, в котором для получения конкретного ответа не хватает одной или нескольких величин или каких-то указаний на свойства объекта или его связи с другими объектами. Решить неопределённую задачу значить указать множество значений искомой величины. Например, задача «В треугольнике одна сторона имеет длину 5 см, а другая 8 см. Найдите длину третьей стороны» не имеет решения, так как в ней не хватает данных. Какой может быть длина третьей стороны? Неравенство треугольника подскажет ответ: 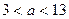 .
.
Задачи с параметрами можно рассматривать как частные случаи неопределённых задач.
Опишем основные трудности, возникающие при решении неопределенных задач.
1) Трудно оценить степень неопределенности задачи и вообще узнать заведомо, является ли задача неопределенной. Есть задачи, которые маскируются под неопределенные, но решаются однозначно. Не всегда неполнота информации, как ее воспринимает человек, соответствует объективной неопределенности задачи.
|
|
|
Может возникнуть ситуация, когда данных в общем случае недостаточно, но именно эти данные представляют частный случай, и решение находится однозначно. Например, можно ли определить вид треугольника, если известны его периметр 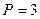 и площадь
и площадь 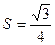 ? В общем случае, данных недостаточно. Так, треугольники со сторонами 3, 2, 2 и
? В общем случае, данных недостаточно. Так, треугольники со сторонами 3, 2, 2 и 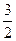 ,
, 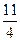 ,
, 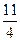 . имеют одинаковые периметр
. имеют одинаковые периметр 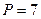 и площадь
и площадь 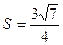 . Первый треугольник – тупоугольный, а второй – остроугольный. Но данных
. Первый треугольник – тупоугольный, а второй – остроугольный. Но данных 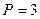 и
и 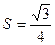 для определения треугольника достаточно, так как этим условиям удовлетворяет лишь равносторонний треугольник со стороной равной 1.
для определения треугольника достаточно, так как этим условиям удовлетворяет лишь равносторонний треугольник со стороной равной 1.
2) Иногда с трудом удается однозначно описать все множество решений или класс объектов, которые удовлетворяют условию.
3) При решении неопределенных задач в большинстве случаев приходится доопределять условие задачи в начале процесса решения, до того, как будет описано множество решений задачи. Трудность и состоит в том, чтобы не слишком сузить круг объектов, удовлетворяющих ограничениям, когда задачу уже невозможно будет решить, или не оставлять задачу слишком неопределенной, что также не поможет продвижению к цели.
Неопределенные задачи требуют от ученика мобилизации практически всего набора знаний, умения анализировать условие, строить математическую модель решения, находить данные к задаче "между строк" условия. Использование задач указанного типа поможет преодолению некоторых трудностей, возникающих в процессе поиска решения задачи, подготовки к «открытию» способа решения. С помощью неопределенных задач создается представление о вариативности решения или ответа к задаче, о путях выбора рационального способа решения.
|
|
|
Опишем особенности процесса решения неопределенной задачи.
На начальном этапе, как и при решении обычной определенной задачи, осуществляется анализ условия и требования задачи. Не во всех случаях после этого учащиеся приходят к пониманию, что задача имеет не одно решение.
При решении неопределенной задачи возможно прохождение по одному из двух путей:
1) Можно считать задачу определенной и получить ответ, зависящий от параметров. Затем исследовать полученное решение.
2) Сделать задачу определенной, самостоятельно введя некоторые ограничения на объекты, рассматриваемые в задаче. То есть возникает задача доопределения ограничений. Причем, можно сузить поле поиска так, что решить заново сформулированную задачу будет невозможно, или, наоборот, можно оставить задачу неопределенной после введения недостаточного количества ограничений.
Например, чтобы решить задачу: «Дана прямая 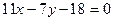 . Напишите уравнение некоторой окружности, касающейся данной прямой» можно составить систему уравнений прямой и окружности в общем виде, а затем наложить условия, которые позволят утверждать, что система имеет единственное решение, зависящее от нескольких параметров: двух координат центра или радиуса и одной координаты центра. В условии задачи требуется найти уравнение всего лишь некоторой окружности, то есть достаточно из множества всех таких окружностей выбрать одну. При этом желательно освободиться от громоздких вычислений.
. Напишите уравнение некоторой окружности, касающейся данной прямой» можно составить систему уравнений прямой и окружности в общем виде, а затем наложить условия, которые позволят утверждать, что система имеет единственное решение, зависящее от нескольких параметров: двух координат центра или радиуса и одной координаты центра. В условии задачи требуется найти уравнение всего лишь некоторой окружности, то есть достаточно из множества всех таких окружностей выбрать одну. При этом желательно освободиться от громоздких вычислений.
Критерием определенности геометрической задачи может быть условие определенности геометрической фигуры. Например, n -угольник определен своими 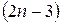 независимыми элементами. (Сколько нужно знать независимых элементов, чтобы определить треугольник, четырехугольник, пятиугольник?) Таким образом, количество данных элементов в задаче поможет сразу сделать предположение о степени ее определенности. Далее обязательно следует проверить независимость данных элементов. Например, для определения тетраэдра необходимо шесть независимых элементов, а правильного многогранника – всего лишь два независимых элемента.
независимыми элементами. (Сколько нужно знать независимых элементов, чтобы определить треугольник, четырехугольник, пятиугольник?) Таким образом, количество данных элементов в задаче поможет сразу сделать предположение о степени ее определенности. Далее обязательно следует проверить независимость данных элементов. Например, для определения тетраэдра необходимо шесть независимых элементов, а правильного многогранника – всего лишь два независимых элемента.
Определенность фигуры условием задачи не всегда является очевидной. Например, в задаче «Найти стороны четырехугольника, если один из его углов равен 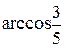 , радиус описанной окружности
, радиус описанной окружности 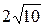 см, а радиус вписанной окружности 3 см» даны всего три элемента из пяти, необходимых для однозначного задания пятиугольника. На самом деле таких элементов пять: суммы противоположных сторон равны, суммы противоположных углов равны и три данных элемента.
см, а радиус вписанной окружности 3 см» даны всего три элемента из пяти, необходимых для однозначного задания пятиугольника. На самом деле таких элементов пять: суммы противоположных сторон равны, суммы противоположных углов равны и три данных элемента.
|
|
|
Однако из того, что фигура неопределенна, не следует неопределенности задачи. Например, в задаче: «Около треугольника АВС описана окружность радиуса R. 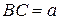 . Найдите угол, лежащий против данной стороны» треугольник АВС не определен, но угол найти можно. Или в задаче: «В пятиугольнике AВCDE
. Найдите угол, лежащий против данной стороны» треугольник АВС не определен, но угол найти можно. Или в задаче: «В пятиугольнике AВCDE 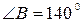 ,
, 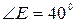 , АС – биссектриса
, АС – биссектриса 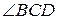 , AD – биссектриса
, AD – биссектриса 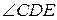 ,
, 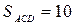 см2. Найдите площадь ABCDE» даны только пять (из семи) независимых элементов пятиугольника. То есть геометрическая фигура неопределенна, и мы не сможем, к примеру, найти величину
см2. Найдите площадь ABCDE» даны только пять (из семи) независимых элементов пятиугольника. То есть геометрическая фигура неопределенна, и мы не сможем, к примеру, найти величину 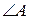 или длину диагонали AD, но площадь пятиугольника вычислить сможем.
или длину диагонали AD, но площадь пятиугольника вычислить сможем.
Задачи переопределённые – задачи, в которых имеются лишние данные, не нужные для решения, а лишь маскирующие способ решения задачи. Данные в таких задачах могут быть противоречивыми и выявление этой противоречивости или непротиворечивости является обязательным элементом решения переопределенной задачи. Задачи этого типа требуют от ученика умения анализировать условие, находить в нём нужные данные и отбрасывать ненужные. Причём, «ненужными» у разных учеников могут быть разные величины. Например, в задаче «Найдите площадь прямоугольника по стороне, диагонали и углу между диагоналями» одни ученики будут искать ответ половиной произведения диагоналей на синус угла между ними (тем самым сторона становится лишним данным), другие получат ответ, произведением сторон, предварительно вычислив вторую сторону по теореме Пифагора (здесь угол становится лишним данным). Возможен и третий вариант, когда лишним данным станет диагональ.
Рассмотрим задачу: «На окружности основания цилиндра отмечены точки А и В так, что дуга АВ равна 600. На окружности другого основания отмечены точки C и D так, что CD – диаметр, перпендикулярный прямой АВ. Найдите объем пирамиды ABCD, если объем цилиндра равен 32 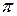 , а плоскость ACD образует с плоскостью основания цилиндра угол 450».
, а плоскость ACD образует с плоскостью основания цилиндра угол 450».
|
|
|
| 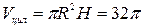 , то есть , то есть 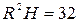 .
Отметим точку К так, что АК=ВК.
Тогда .
Отметим точку К так, что АК=ВК.
Тогда 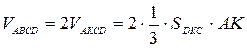 . .
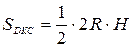 , , 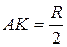 . Значит, . Значит, 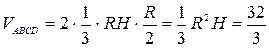 . .
|
При решении этой задачи мы не использовали угол 450. Следовательно, эта задача переопределенная. Если использовать все данные, то решение громоздкое, некрасивое.//
Таким образом, переопределенные задачи позволяют учащимся высказать прогноз способа решения, в соответствии с ним выбрать необходимые данные и проверить правильность решения, сравнив ответы.
Для нереальных задач характерным является то, что они могут «формально» иметь ответ, но он будет противоречить здравому смыслу. Как в знаменитых строчках С. Маршака «…и получается в ответе два землекопа и две третьих».
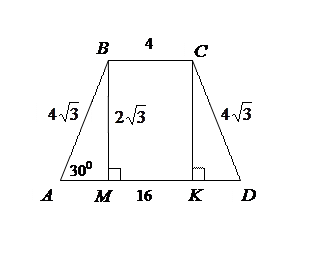
Следует различать нереальные задачи и противоречивые. Последние содержат в условии противоречие между данными. Например, задача: «В равнобедренную трапецию ABCD можно окружность. Найдите площадь трапеции, если ее основания равны 4 и 16 см, а острый угол при основании равен 300» переопределена.
         
| Решим ее, считая, что «острый угол при основании равен 300» лишнее условие. Тогда вписать в трапецию окружность можно лишь при условии, что 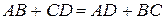 .
Так как .
Так как 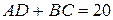 , а , а 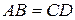 , то , то 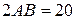 , , 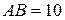 . .
|
Из прямоугольного треугольника АВМ 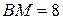 . А площадь трапеции равна
. А площадь трапеции равна 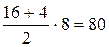 . В данном случае имеем противоречие с условием, так как острый угол при основании не равен 300.
. В данном случае имеем противоречие с условием, так как острый угол при основании не равен 300.
| Решая задачу, считая лишним условием, что «в трапецию можно вписать окружность», получаем: 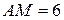 , , 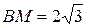 , , 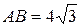 .
Тогда не выполняется условие, что .
Тогда не выполняется условие, что 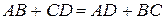 . Следовательно, в трапецию нельзя вписать окружность. . Следовательно, в трапецию нельзя вписать окружность.
|
Если в исходной задаче заменить условие «острый угол при основании равен 300» на «синус острого угла при основании трапеции равен 0,8», то получим переопределенную задачу.
Решить противоречивую задачу – значит найти противоречивость в условии. Например, прочитав текст задачи: «Катеты прямоугольного треугольника равны 3 и 4 см, а высота, проведенная к гипотенузе, – 2 см. Найдите отрезки, на которые делит высота гипотенузу», многие учащиеся тут же начинают вычислительную работу. Но такого треугольника не существует.
Поскольку противоречивость задачи не всегда бросается в глаза, необходимо выполнять проверку полученного ответа. Некоторые из задач этого типа позволяют выявить противоречие данных еще при анализе условия, в результате чего процесс решения становится излишним. Достаточно частое повторение таких ситуаций приведёт учащихся к необходимости анализировать условие перед началом решения, чтобы избавить себя от лишней работы.
В задачах провоцирующего характера условия содержат побудители, подталкивающие к выбору ошибочного пути решения или неверного ответа. Например, условие задачи «Сколько граней имеет шестигранная пирамида?» навязывает неправильный ответ – 6. (Правильный ответ – 8 граней.)
М.И. Зайкиным, В.А. Колосовой // выделены типы провоцирующих задач.
· Задачи, условия которых в той или иной форме навязывают неверный ответ.
· Задачи, условия которых тем или иным способом подсказывают неверный путь решения.
· Задачи, вынуждающие придумывать, составлять, строить такие математические объекты, которые при заданных условиях не могут иметь места.
· Задачи, вводящие в заблуждение из-за неоднозначности трактовки терминов, словесных оборотов, буквенных или численных выражений.
· Задачи, условия которых допускают возможность опровержения семантически верного решения синтаксическим или иным нематематическим способом.
Н.С. Майкова // считает, что разновидности провоцирующих задач зависят от видов провокации, и выделяет следующие виды провокаций: 1) ошибка в рассуждении, 2) действие по аналогии, 3) противоречие в условии, 4) интерпретация ответа задачи, 5) неоднозначное решение.
1. Верно ли, что 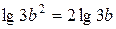 . (Нет, не верно, так как
. (Нет, не верно, так как 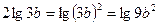 .)
.)
2. Найдите площадь треугольника АВС, если: 1) 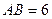 см,
см, 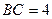 см,
см, 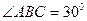 ; 2)
; 2) 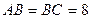 см,
см, 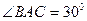 . (Во второй задаче дан угол, лежащий против одной из известных сторон.)
. (Во второй задаче дан угол, лежащий против одной из известных сторон.)
3. Периметр треугольника равен 6 см, а его стороны относятся как 1:2:3. Чему равна средняя по величине сторона? (Треугольник не существует, так как не выполняется неравенство треугольника.)
4. В прямоугольнике ABCD со сторонами 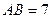 см и
см и 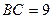 см от точек А и С в направлении точки В отложили равные отрезки, получив соответственно точки L и K. Площадь нового прямоугольника LBKN равна 35 см2. Найдите длину отрезка АL.
см от точек А и С в направлении точки В отложили равные отрезки, получив соответственно точки L и K. Площадь нового прямоугольника LBKN равна 35 см2. Найдите длину отрезка АL.
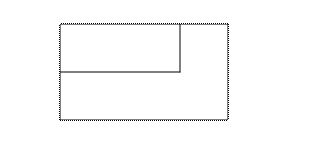
| Обозначив длину отрезка A L через х см, получим 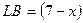 см, см, 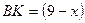 см. Площадь прямоугольника LBKN будет равна см. Площадь прямоугольника LBKN будет равна 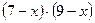 или 35 см2. Уравнение или 35 см2. Уравнение 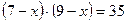 имеет корни имеет корни 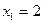 , , 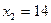 . .
|
Учащиеся отбрасывают второй корень, не задумываясь, почему получился такой нереальный результат: сторону уменьшили на длину большую длины самой стороны. Во втором случае точка L будет находиться на продолжении отрезка АВ за точку В, а точка К – на продолжении отрезка СВ за точку В.
5. Чему равен периметр параллелограмма, если биссектриса одного из его углов делит сторону параллелограмма на отрезки 7 см и 14 см?
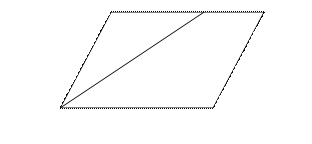
| Возможны два случая:
1) 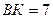 см, см, 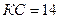 см;
2) см;
2) 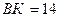 см, см, 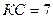 см; см;
|
Феномен провоцирующих задач изучен не достаточно: нет ни их сколько-нибудь целостного описания, ни их систематического представления в виде подборок, систем или сборников, не охарактеризованы побудители, подталкивающие к выполнению ошибочных действий или выбору неправильного ответа, не предложены типологии провоцирующих задач, не разработана методика их использования в процессе обучения. // Включение таких задач в процесс обучения математике способствует развитию критичности мышления. Основной способ убеждения учащихся в неправильности решения задач указанного типа – приведение контрпримеров.
Я.И. Груденов // называя «контрпримером» любую задачу, которая провоцирует учащихся на ошибку, помогая выявить и устранить имеющиеся у них ошибочные ассоциации, указывает на дидактическую значимость провоцирующих задач.
Например, рассмотрим систему задач по теме «Подобные треугольники».
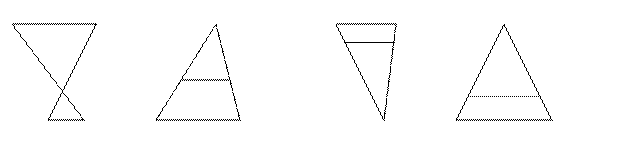
При закреплении признака подобия треугольников по двум углам учащимся предлагается сначала три задачи одного типа «Найдите подобные треугольники и докажите их подобие». Четвертая задача – провокационная: «Треугольники АВС и КВМ подобны. Параллельны ли стороны АС и КМ?» Обратное утверждение к теореме: «Прямая, параллельная стороне треугольника, отсекает от него треугольник, подобный данному» – не верно, поэтому стороны АС и КМ могут быть не параллельными. Убедить в этом учащихся поможет контрпример, изображенный на рисунке.
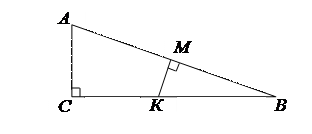
| Треугольники АВС и КВМ подобны. А стороны АС и КМ не параллельны. |
Провоцирующие задачи, включаемые в систему упражнений, помогают усиливать интерес учащихся, их внимание, активизировать мыслительную деятельность.
Даже краткая характеристика нестандартизированных задач доказывает их значимость для развития критичности мышления, комбинаторных способностей учащихся, создания ситуаций побуждения к более вдумчивому анализу заложенной в задаче информации и ее структурированию.
Задачи указанного типа приближены к жизненно-практическим условиям, так как любая жизненная ситуация как правило имеет несколько вариантов исхода в зависимости условий, от отношений между ними. Решение практических задач требует «нахождения» (выбор, оценку, привлечение) данных.
Нестандартизированные задачи создают условия для выработки собственного взгляда на ситуацию и переносят акцент с самого процесса усвоения знаний на их осмысление, наполнение личностным смыслом, что, в свою очередь, обеспечивает более эффективное усвоение знаний.
Детальный анализ условия нестандартизированных задач влечет к необходимости выполнения «прогностических» шагов. Так, переопределённые задачи в соответствии с гипотезой решения требуют выбора минимального числа «нужных» данных. Противоречивые и провоцирующие задачи заставляют делать проверку решения. Неопределённые задачи требуют актуализации знаний об объекте задачи, о связях его с другими математическими объектами, которые могут оказаться полезными при получении диапазона изменения искомой величины.
Однако подавляющее большинство учебных задач не содержат лишних или противоречивых данных, а тем более трудно встретить задачу, в которой не хватает данных для решения. Если такие задачи «попадаются», то в основном по недосмотру автора. При таком подходе учащиеся привыкают к защищенности и в большинстве случаев проводят поверхностный анализ условия.
Неиспользование таких задач в практике объясняется рядом причин:
1. Отсутствием нестандартизированных задач в школьных учебниках.
2. Неготовностью учащихся к решению указанного типа задач.
3. Неразработанностью методики включения нестандартизированных задач в процесс обучения математике.
Остановимся на решении последней проблемы, рассмотрев иерархичность использования нестандартизированных задач и последовательность их включения в процесс решения определенных задач.
На первых этапах должна преследоваться цель – доказать необходимость анализа условия задачи для построения предполагаемого пути ее решения. На этом этапе можно использовать любые задачи, создавая ситуации побуждения к более вдумчивому анализу заложенной в задаче информации, к нахождению информации, наталкивающей на путь решения задачи. Переопределенные задачи требуют выбора данных. Нереальные и провоцирующие задачи ставят учащихся в «тупик».
После мотивационного этапа необходима адаптация к новым задачам.
При введении переопределенных задач на первых порах следует предупреждать учащихся о наличии избыточных данных, предлагать им найти такие данные, постепенно переходя от задач простых к задачам, в которых избыточные данные не сразу бросаются в глаза. Когда учащиеся приобретут некоторые навыки решения переопределенных задач, можно перейти к введению таких задач уже без предупреждения о наличии избыточных данных, чередуя эти задачи с традиционными определёнными задачами. Таким образом, не зная, имеется ли в условии задачи лишнее данное или нет, но, подозревая, что оно может быть, учащиеся к каждой задаче будут подходить критически, что вызовет большую, чем в традиционных условиях, необходимость внимательного анализа условия задачи и различных подходов к её решению.
На некотором этапе переопределённые задачи, предлагаемые учащимся, могут стать противоречивыми. Использование таких задач постепенно приучит их к тому, что обнаруженное в условии лишнее данное не следует игнорировать, но следует проверять его на противоречивость. Кроме того, использование задач с противоречивыми данными позволит учащимся заметить (не без помощи учителя) полезность вдумчивого анализа условия, в результате которого можно выявить противоречивость и тем самым не искать решения, т.е. облегчить себе работу. А поскольку никогда не ясно, есть ли противоречие в условии задачи или нет, то вдумчивому анализу будут подвергаться условия всех задач.
Когда переопределённые задачи станут привычными, и не будут вызывать у учащихся настороженности и протеста, можно перейти к решению неопределённых задач, снова же вначале предупреждая учащихся о том, что в условии задачи некоторых данных не хватает и, предлагая им указать, каких.
Учащимся полезно показывать процесс получения из определенной задачи переопределенную, неопределенную и нереальную задачи методом варьирования условий.
Последовательное, постепенно усложняющееся варьирование условия задач является основным принципом, определяющим построение системы упражнений при обучении решению типовых определенных задач.
Вначале – варьирование условия касается самых несущественных его сторон, непосредственно не влияющих на применение основного приёма решения, а именно сюжета задачи и числовых величин. Основная цель – закрепление в памяти учащихся приёма решения задач данного типа и выработка умения распознавать за различной внешней фабулой задачи её одинаковую логическую структуру.
На следующем этапе целесообразно вводить в условия задач дополнительные элементы, увеличивая количество числовых данных. Введение дополнительных данных никак не влияет на использование основного приёма решения, но для учащихся всё же создаётся новая ситуация, требующая от них умения вычленить ту часть условия, которая определяет применение типового приёма и в ходе действий при решении задачи найти ему правильное место.
В дальнейшем уже можно прибегать к такому варьированию условий задачи, которое требует видоизменения самого типового приёма. Такого рода варьирование способствует выработке умений перестраивать известные способы решения в соответствии с изменением условий задачи.
И, наконец, последнее видоизменение условия определенной задачи – составлять условие, чтобы некоторых данных в них не хватало. С учётом предыдущего опыта учеников по решению задач, этот тип задач, во-первых, будет для них несколько сложным и новым, во-вторых, решая задачи такого типа, ученики более наглядно осознают скрытые свойства объекта задачи, уясняют более детально динамические соотношения между понятиями и определениями, применяемыми при решении данной задачи. Эту цель преследуют и задачи с несформированным требованием.
Вопросы и задания
1. Какие виды нестандартизированных задач существуют? В чем их отличительные особенности?
2. Каким образом могут ли быть получены нестандартизированные задачи из стандартизированных?
3. Дана нестандартизированная задача: «Найдите наименьший возможный радиус круга, которым можно накрыть треугольник со сторонами 10, 11 и 15 см». Определите ее вид и опишите методику ее решения на уроке.
4. Дана задача: «В основании пирамиды лежит прямоугольный треугольник с катетами 6 и 8 см. Все боковые ребра пирамиды равны 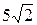 см. Найдите объем пирамиды». Составьте из этой задачи различные виды нестандартизированных задач.
см. Найдите объем пирамиды». Составьте из этой задачи различные виды нестандартизированных задач.
5. Решите задачи: 1) В арифметической прогрессии первый член равен 800, а разность равна -25. Сумма скольких членов равна 5700? 2) Турист поднимается в гору, в первый час он достиг высоты 800 м, а каждый следующий час поднимался на высоту, на 25 м меньшую, чем в предыдущий. За сколько часов он достигнет высоты в 5700 м? Дайте интерпретацию ответов.
6. Верно ли?
1) Если прямая перпендикулярна двум прямым лежащим в плоскости, то она перпендикулярна и самой плоскости.
2) Плоскости параллельные одной прямой параллельны.
3) Если плоскость 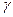 пересекает плоскости
пересекает плоскости 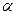 и
и 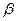 по параллельным прямым, то плоскости
по параллельным прямым, то плоскости 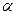 и
и 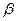 параллельны.
параллельны.
4) Два равных отрезка, заключенные между параллельными плоскостями, параллельны.
5) Если прямая лежит в одной из перпендикулярных плоскостей, то она перпендикулярна линии пересечения этих плоскостей.
Опровергая утверждение, приведите контрпример.
7. Составьте провоцирующие задачи по любой теме школьного курса математики.
8. Рассмотреть примеры провоцирующих задач, приведенных в § 32 книге: Груденов Я.И. Совершенствование методики работы учителя математики: Кн. для учителя. – М.: Просвещение, 1990.
|
|
|
|
|
Дата добавления: 2014-12-16; Просмотров: 3885; Нарушение авторских прав?; Мы поможем в написании вашей работы!