Определение случайной погрешности

Случайные погрешности приводят к тому, что наблюдаемые значения измеряемой величины при многократных измерениях случайным образом рассеяны относительно ее истинного значения. Тогда действительное значение находится как наиболее вероятное из серии опытов, а погрешность характеризуют шириной интервала, который с заданной вероятностью включает истинное значение. Математическое обоснование этих положений дается в теории вероятностей, применение которой для обработки результатов измерений приведено в литературе 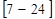, а непосредственное применение к работам физического практикума в литературе .

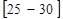Очень часто студенты и школьники находят погрешность измерения по формуле

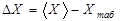, (6.2)

где 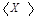- полученное в процессе измерения среднее значение величины, а 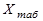- значение, взятое из справочника, или рассчитанное из теоретических представлений. Такое определение погрешности является грубой ошибкой, так как целью эксперимента, как было показано выше, является проверка теоретических представлений и уточнение табличных данных.

Кроме того, часто погрешность вычисляется как среднее значение отклонений отдельных результатов измерений от среднего значения по формуле

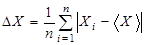. (6.3)

Согласно такому подходу, любое значение погрешности появляется одинаково часто, т.е. разные по величине погрешности считаются равновероятными. Этот метод можно использовать в лабораторных работах при малом числе измерений.

Однако случайные погрешности не являются равновероятными. Они требуют для своего определения статистической обработки результатов измерения. Поэтому представляется необходимым рассмотреть содержание статистической обработки результатов измерений. В основе статистической теории погрешностей лежат следующие положения:

1) при большом числе измерений наблюдаются случайные погрешности одинаковой величины, но разного знака, т. е. погрешности, как в сторону уменьшения, так и в сторону увеличения, встречаются одинаково часто;

2) большие (по абсолютной величине) погрешности встречаются реже, чем малые, т.е. вероятность появления погрешности уменьшается с ростом величины погрешности;

3) погрешности измерений могут принимать непрерывный ряд значений.

Распределение случайной величины, которое подчиняется перечисленным свойствам, называется нормальным распределением. Для оценки разбросов отдельных значений случайной величины с нормальным распределением или отдельных отсчетов в теории нормального распределения выбирается выборочное среднее квадратичное отклонение отсчетов, которое вычисляется по формуле:

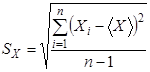. (6.4)

Оценка величины погрешности одного измерения, определяемая формулой (6.4) очень важна. Однако для измерения важной задачей является определение, с какой точностью среднее значение измеряемой величины соответствует искомой величине. Эта задача возникает в связи с тем, что среднее значение может быть получено из разных измерений. Например, среднее значение может быть получено при различном числе измерений. Поэтому эмпирическое среднее значение также является случайной величиной, которая также может описываться функцией распределения. Соответствующая этой функции величина среднего квадратичного отклонения 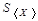определяется, как показано в теории вероятностей по формуле:

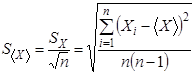(6.5)

Эта величина называется выборочным средним квадратичным отклонением среднего значения или стандартной ошибкой.

Как видно из формулы стандартной ошибки (6.5), она уменьшается с ростом числа измерений и точность результата возрастает, что и соответствует предыдущим рассуждениям.

Рассмотренные выше формулы для определения ошибки измерения используют характеристики нормального распределения случайной величины. Однако неизвестно, по какому закону распределены результаты измерений. Поэтому эти оценки являются приближенными. В связи с этим возникает необходимость анализа этого подхода к определению погрешности измерения. Для такого анализа можно использовать известное в теории вероятностей понятие доверительного интервала. Пусть величина 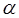равна вероятности того, что результат измерения – среднее значение – отличается от истинного значения на величину не большую 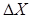. В теории вероятностей эта фраза записывается следующим образом:

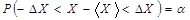или

.

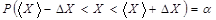Величина 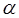называется доверительной вероятностью (надежностью) результата серии наблюдений. Она показывает вероятность, с которой доверительный интервал включает истинное значение измеряемой величины.

Доверительным интервалом называется интервал значений 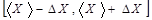, который с заданной степенью достоверности включает в себя истинное значение измеряемой величины. Геометрическое представление этого интервала дано на рисунке 1.

Таким образом, для определения случайной погрешности необходимо найти или задать два числа: а именно величину самой случайной погрешности или доверительного интервала и величину доверительной вероятности.

Для любой величины доверительного интервала можно рассчитать доверительную вероятность. Для этого используется функция Лапласа, которая также называется интегралом вероятностей. Функция Лапласа имеет вид:

,

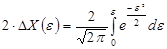где 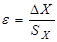. Чаще всего, при решении задач используют табличные значения функции Лапласа. Эти значения приведены в таблице 1.

Результаты этой таблицы показывают, что средней квадратичной ошибке 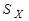соответствует доверительная вероятность 0,68, удвоенной средней квадратичной ошибке 2 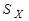соответствует доверительная вероятность 0,95, а утроенной средней квадратичной ошибке 3 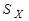– 0,997.

Таблица 1

Доверительные вероятности 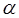для доверительного интервала, выраженного в долях средней квадратичной ошибки 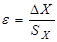. Функция Лапласа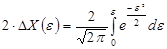

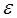
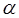
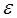
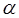
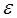
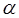
		1,2	0,77	2,6	0,990
0,05	0,04	1,3	0,80	2,7	0,993
0,1	0,08	1,4	0,84	2,8	0,995
0.15	0,12	1,5	0,87	2,9	0,996
0,2	0,16	1,6	0,89	3,0	0,997
0,3	0,24	1,7	0,91	3,1	0,9981
0,4	0,31	1,8	0,93	3,2	0,9986
0,5	0,38	1,9	0,94	3,3	0,9990
0,6	0,45	2,0	0,95	3,4	0,9993
0,7	0,51	2,1	0,964	3,5	0,9995
0,8	0,57	2,2	0,972	3,6	0,9997
0,9	0,63	2,3	0,978	3,7	0,9998
1,0	0,68	2,4	0,984	3,8	0,99986
1.1	0,73	2,5	0,988	3,9	0,99990
				4,0	0,99993

Случайную погрешность принято определять как полуширину доверительного интервала. Размер доверительного интервала задается в виде значения кратного выборочному среднему квадратичному отклонению среднего значения 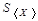, которое определяется по формуле (6.5). Тогда случайная погрешность многократных измерений определяется формулой:

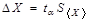, (6.6)

Дата добавления: 2014-12-16