Определенный интеграл

Решение.

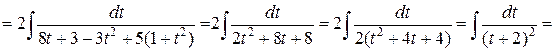
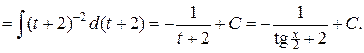v

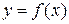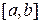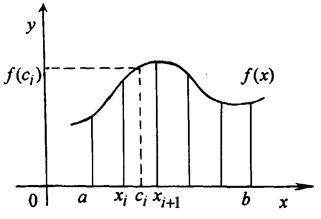
Пусть дана функция непрерывная на отрезке . Разобьем этот отрезок произвольным образом на n частей точками 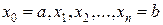(рисунок 7.1). Длины соответствующих отрезков обозначим 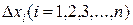. Произвольным образом выберем точки 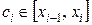и составим сумму

.

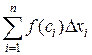Эта сумма называется интегральной суммой для функции 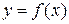на отрезке 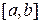. Каждое слагаемое суммы приближенно представляет площадь прямоугольника с основанием 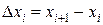и высотой .

Рисунок 7.1

Поэтому вся интегральная сумма будет приближенно равна площади области, ограниченной отрезком 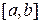оси OX, кривой 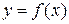и прямыми , т.е. площади криволинейной трапеции.

Определение. Если существует предел при суммы, не зависящий ни от способа разбиения отрезка 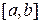на части, ни от выбора точек внутри 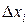, то этот предел называется определенным интегралом от функции 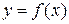на отрезке 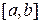и обозначается . Итак,

.

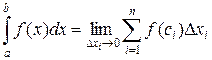Из предыдущих рассуждений следует, что если 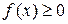, то определенный интеграл равен площади указанной криволинейной трапеции. Вычисление определенного интеграла осуществляется по формуле Ньютона-Лейбница

,

где — одна из первообразных функции .

Например,

. v

Если для вычисления определенного интеграла требуется сделать подстановку вида x =j(t) или j (x)= u, то, переходя под интегралом к новой переменной, находим из данной подстановки пределы изменения этой переменной и вычисляем вновь полученный определенный интеграл с новыми пределами.

Пример. Вычислить определенный интеграл .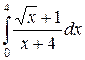

Решение.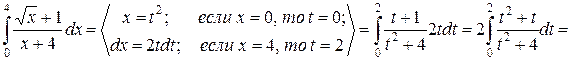

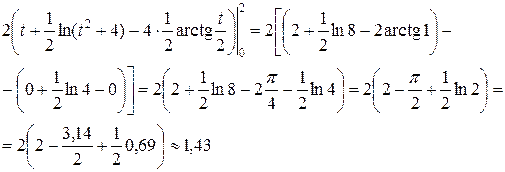
При вычислении этого интеграла были применены формулы

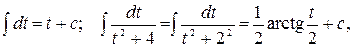
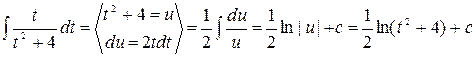. v

Дата добавления: 2014-12-17