Евклидов алгоритм

Алгоритм Мэсси

S₁ = α⁶, S₂ = α⁵, S₃ = α, S₄ = α

i = 0: σ(x)=1, ℓ=0, ρ(x)=x

i = 1: σ(x)=1, ℓ=0, ρ(x)=x

σ_new(x)=σ(x) +dρ(x)=1+α⁶x, 2l=0<i, ℓ= i - ℓ=1,

ρ(x)= σ(x)/d= α^-6= α,

ρ(x)= x ρ(x)= αx, σ(x) = σ_new(x).

i=2: d=S₂ + 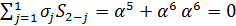, ρ(x)= x ρ(x)= αx²

=

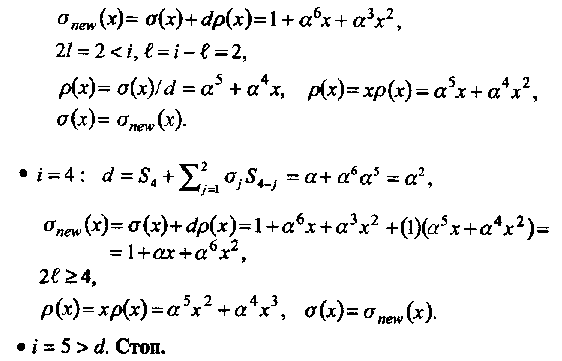
• Начальные условия:

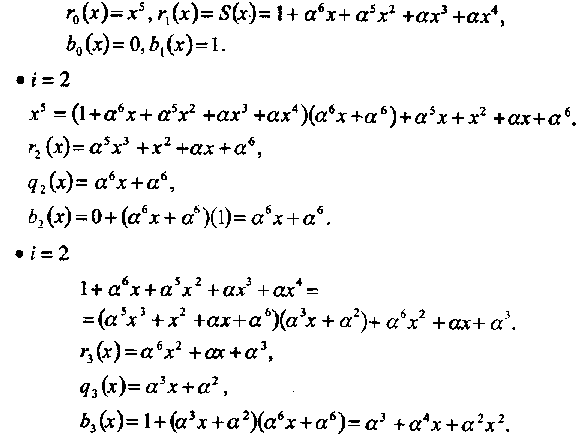
Алгоритм останавливается, так как deg[r₃(x)] = 2 = t_d. Следовательно, σ (х) = α³ + α ⁴х + α ²х² = α³(1 + α х + α ⁶х²).

Все рассмотренные алгоритмы дали одинаковое, с точностью до константного множителя, решение для многочлена локаторов ошибок:

Таким образом, ошибки произошли на позициях j₁ = 2 и j₂ = 4. Координаты ошибок находятся с помощью процедуры Ченя как обратные величины корней многочлена локаторов ошибок σ (х). Заметим, что σ’ (х) = 0, так как в поле GF(2^m) характеристики 2 справедливо равенство 2а = а+а=0.

Для вычисления значений ошибок (любым из рассмотренных алгоритмов) необходим многочлен значений ошибок (4.5),

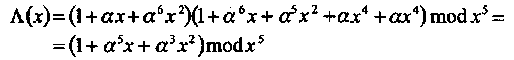
Важно отметить, что алгоритм Евклида вычисляет σ (х) и Λ(х) одновременно, как σ (х) = b_last (x) и Λ(х) = r_last(x) (см. раздел 3.5.4, ЕА). Для проверки этого утверждения заметим, что

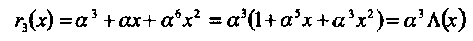
Если локаторы ошибок известны, то значения ошибок, найденные из уравнения (4.4). равны

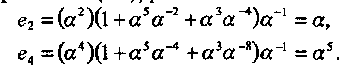
Таким образом, е(х) = α х² + α⁵x⁴ и декодированное слово равно

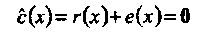
Исправлены две ошибки.

Заметим, что оба полинома, найденные алгоритмом Евклида, имеют одинаковый константный множитель β, т.е. алгоритм находит βσ(х) и βΛ(х) с некоторым множителем β s w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 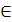GF(2^m). Тем не менее, оба полинома имеют те же самые корни, что иполиномы, вычисленные алгоритмами БМА или PGZ. В результате и значения ошибок совпадают.

В большинстве программ, моделирующих процедуры кодирования и декодирования PC кодов, используется следующий эквивалентный способ определения значений ошибок [LC]. Пусть

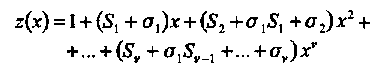(4.6)

Тогда значения ошибок равны [Вег]

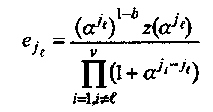(4.7)

где 1 .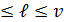

Еще одна альтернатива алгоритму Форни, для малых значений t_d, состоит в следующем способе вычисления значений ошибок. Значения ошибок 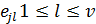связаны с синдромами S_i системой линейных уравнений:

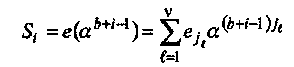(4.8)

где 1 .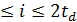

Каждая v 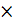v подматрица, образованная (известными) членами α^{(b+i-1) jℓ} образуют матрицу Вандермонда. Если известно положение всех v ошибок, то любое подмножество v уравнений (4.8) может быть использовано для определения значений ошибок. Например, используя первые v синдромов, получаем следующую систему линейных уравнений,

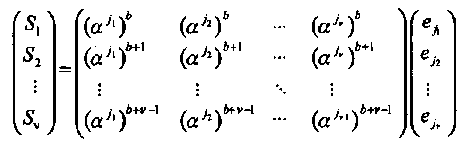(4.9)

решение которой может быть найдено над полем GF(2^m).

Пример 42. Рассмотрим тот же код PC и принятый многочлен из Примеров 40 и 41. Из (4.9) получаем

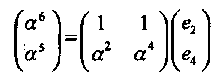
Определитель 2x2 матрицы равен ∆ = α⁴ + α ² = α. Отсюда следует, что

и

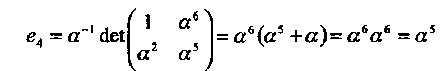
Полученные значения ошибок совпадают с теми, которые вычислены по алгоритму Форни. Подчеркнем еще раз, что этот способ может быть применен при исправлении только очень небольшого числа ошибок.

4.3.1. Комментарий к алгоритмам декодирования

В отличие от БМА алгоритм Евклида (ЕА) использует все синдромы уже на первом шаге процедуры. Однако, по числу операций в конечном поле алгоритм Берлекэмпа-Мэсси (БМА) обычно эффективнее ЕА. С другой стороны, каждый шаг ЕА имеет идентичную структуру, что приводит к более эффективной аппаратной (микросхемной) реализации. Кроме того, три рассмотренных метода декодирования для (двоичных и недвоичных) кодов БЧХ являются неполными, так как исправляют ограниченное число ошибок — декодирование с ограниченным расстоянием. Вследствие этого рассмотренные алгоритмы способны обнаруживать ситуации, которые превышают их корректирующую способность.

Рассмотренные алгоритмы исправляют все комбинации ошибок ограниченного веса (до половины кодового расстояния). Многие из комбинаций ошибок большего веса не могут быть исправлены этими алгоритмами, но обнаруживаются и приводят к отказу от декодирования. В зависимости от конкретного применения кода в этом случае, либо выдаются принятые из канала информационные символы систематического кода, либо все слово заменяется символом (сигналом) стирания. Обнаружение неисправимых комбинаций ошибок происходит, либо в процедуре Ченя, когда хотя бы один из корней многочлена локаторов ошибок не принадлежит множеству локаторов позиций кодового слова, либо на этапе вычисления синдромов, когда количество нулевых синдромов оказывается больше или равным половине кодового расстояния.

Известны также и другие подходы к декодированию кодов БЧХ, из которых наиболее значительным является использование быстрых алгоритмов дискретного преобразования Фурье над полем GF(2^m). Этот подход к созданию быстрых алгоритмов декодирования исследуется в [Blah], где читатель найдет необходимые подробности.

Рассмотренные выше алгоритмы принято называть декодированием в частотной области, учитывая эквивалентность между вычислением синдрома и преобразованием Фурье над конечным полем. В [Blah, Blah 1*} рассматриваются и другой подход к построению декодеров — декодирование во временной области. Этот вариант декодеров PC кодов требует большего количества операций в поле, но считается более удобным для аппаратной (микросхемной) реализации.

Сравнительно недавно Судан [Sud] предложил (алгебраический) алгоритм, исправляющий ошибки за границей минимального расстояния кода. Этот алгоритм применяется к декодированию PC и, главным образом, АГ кодов. Выходом этого алгоритма является список (ближайших в некоторой метрике) кодовых слов. Алгоритм {декодирования в список) основан на процедурах интерполяции и факторизации многочленов от двух переменных над GF(2^m) и его расширением. Оригинальный алгоритм Судана был позднее улучшен в работе [Gur] и других. Важно, что на основе алгоритма Судана создан алгебраический алгоритм мягкого декодирования кодов PC и близких к ним АГ кодов.

4.3.2. Исправление ошибок и стираний

Для исправления стираний необходимое изменение в процедуре декодирования кодов PC, рассмотренной выше, состоит во введении многочлена локаторов стираний τ(х),

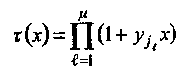
где у_iℓ = а^iℓ, локаторы стираний, 1 ≤ ℓ ≤μ.

По определению, позиции со стираниями известны. Следовательно, требуется определить только значения стертых позиций. Это может быть выполнено, как и раньше, по алгоритму Форни. Можно показать, что в процессе вычисления синдромов на стертых позициях могут быть подставлены произвольные значения символов, так как их значения не влияют на результат декодирования.

Процедура декодирования PC с исправлением стираний и ошибок аналогична исправлению только ошибок с учетом следующих ниже модификаций. Прежде всего, формируется модифицированный синдромный многочлен, или модифицированный синдром Форни,

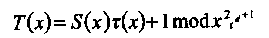(4.10)

Алгоритм БМ применяется для определения многочлена локаторов ошибок с учетом следующих изменений:

1. Рассогласование определяется теперь как

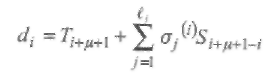(4.11)

где d₀=T_μ+1

2. Условие остановки алгоритма заменяется следующим:

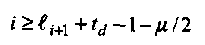
По окончании вычисления σ (х) формируется модифицированный многочлен значений ошибок и стираний, или многочлен значений искажений, равный по определению

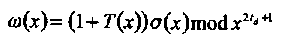(4.12)

Кроме того, вычисляется следующий многочлен локаторов искажений,

(4.13)

С помощью модифицированного алгоритма Форни получаем для значений ошибок:

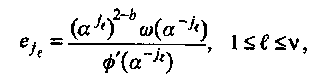(4.14)

и для значений стираний:

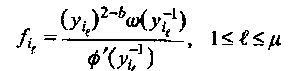(4.15)

Алгоритм Евклида также может быть применен к модифицированному синдрому T(х) для исправления стираний и ошибок. Для этого в алгоритме исправления только ошибок многочлен S(x) заменяется многочленом 1 + Т(х), а в начальных условиях r₀(x) =x^d,d = 2t_d+1, и r₁(x) = 1 + Т(х). Алгоритм останавливается на j-ом шаге, если deg[r_j(x)] ≤ |_(d - 1 +μ)/2_|, и выдает как решение w(х) = r_j(х) и σ (х) = b_j(x).

Пример 43. Пусть С это (15,9,7) код PC над GF(2⁴) с нулями в точках {а, а²,..., а⁶}, где примитивный элемент поля удовлетворяет равенству р(а) =а⁴ + а³ + 1 = 0. Для удобства ниже представлена таблица элементов GF(2^m), упорядоченная по степеням примитивного элемента а, а⁴ + а³ + 1 = 0. Таблица элементов GF(2^m), p(x) = x⁴+x³+1.

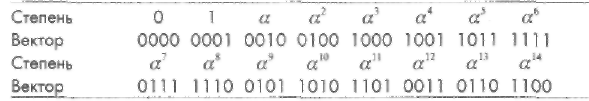
Порождающий многочлен кода С равен

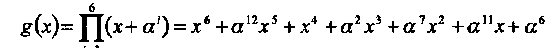
Положим, что ассоциированный с кодовым словом полином равен

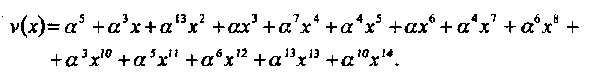
Пусть принятое слово представлено полиномом

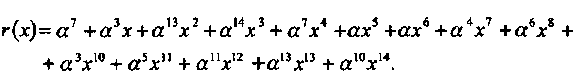
Предположим, что приемник располагает дополнительной информацией о том, что позиции с локаторами а⁰ и а⁵ ненадежны и заявлены как стирания.

Заметим, что многочлен искажений имеет вид е(х) = а¹⁴ + а⁸x³ + а⁵х⁵ + ах¹².

Таким образом, кроме принятого слова r (х) декодеру известны локаторы μ= 2 двух стираний, а⁰ и а⁵. Это позволяет вычислить многочлен локаторов стираний

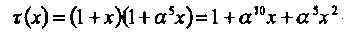(4.16)

Синдромы для принятого слова равны:

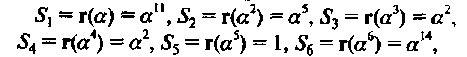
Соответственно, синдромный многочлен равен:

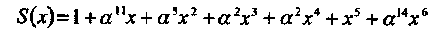(4.17)

Модифицированный синдром (4.10) равен

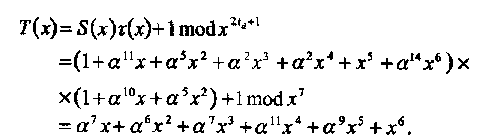
Дата добавления: 2014-11-29