Математических моделей

Применение преобразования Лапласа для анализа

С помощью преобразования Лапласа дифференциальные уравнения могут быть преобразованы в алгебраические, которые гораздо легче анализировать и решать. Преобразование некоторой функции времени по Лапласу заключается во взятии интеграла от этой функции следующего вида:

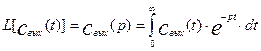
(3.1.12)

где L –символ преобразования Лапласа; 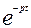- ядро преобразования; 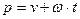– оператор Лапласа (комплексное число); v, w - действительная и мнимая части комплексного числа. Преобразуемая функция 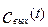называется в этом случае оригиналом, а преобразованная 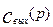- изображением. Рассмотрим несколько примеров применения преобразования Лапласа к некоторым функциям.

Пример 1. Требуется преобразовать по Лапласу функцию вида - 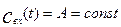Тогда изображение будет иметь вид:

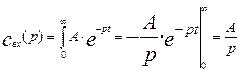(3.1.13)

Пример 2. Требуется преобразовать по Лапласу функцию вида 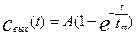при . Подставив данную функцию в равнение(3.1.12), получим:

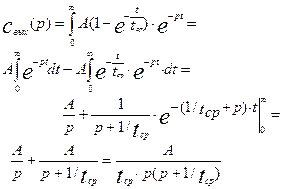(3.1.14)

Для перехода от изображения 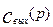к оригиналу 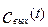используется обратное преобразование Лапласа. Символ обратного преобразования Лапласа L^-1. Провести обратное преобразование Лапласа над функцией 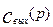– это значит взять интеграл вида:

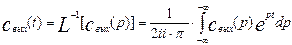(3.1.15)

Для большинства функций значения прямого и обратного преобразования Лапласа известны и приведены в справочных таблицах.

Рассмотрим некоторые свойства преобразования Лапласа:

1. Каждый член уравнения преобразуется отдельно (свойство линейности преобразования)

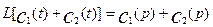(3.1.16)

2. Дифференцированию оригинала в области действительного переменного t соответствует умножению на р в степени, равной порядку производной (при нулевых начальных условиях)

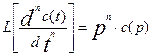(3.1.17)

2. Интегрированию оригинала соответствует деление изображения на переменную р в степени, равной порядку интегрирования (при нулевых начальных условиях).

3. Запаздыванию в области действительного переменного на величину 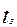соответствует умножение изображение на величину :

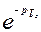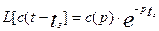(3.1.18)

Преобразование Лапласа тесно связано с понятием передаточной функции W(p). Передаточной функцией объекта называют отношение преобразованной по Лапласу выходной характеристики объекта к преобразованной по Лапласу входной характеристике при нулевых начальных условиях:

(3.1.19)

Из выражения (3.1.19) легко найти связь между выходной и входной характеристиками объекта через передаточную функцию:

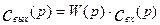(3.1.20)

Для нахождения оригинала функции по ее изображению необходимо выполнить обратное преобразование Лапласа:

(3.1.21)

Если входная величина есть 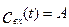, то, учитывая выражение (3.1.21) и формулу (3.1.13), получим:

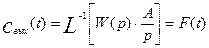(3.1.22)

Изменение во времени выходной характеристики объекта при нанесении на вход ступенчатого возмущения 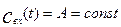, если до нанесения возмущения объект находился в состоянии равновесия, называется кривой разгона, или F – кривой. Следовательно, уравнение (3.1.22) выражает связь кривой разгона с передаточной функцией объекта. Если в качестве входного возмущения используется импульсное возмущение типа функции Дирака d(t), то, учитывая выражение (3.1.21) а также значение преобразованной по Лапласу функции Дирака 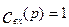, получим для выходной характеристики следующее выражение:

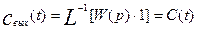(3.1.23)

Изменение выходного параметра объекта во времени при нанесении на вход импульсного возмущения, называется импульсной характеристикой объекта, или С - кривой. Найдем передаточную функцию, а также кривую разгона и импульсную характеристику для объекта, описываемого моделью идеального перемешивания.

Математическая модель идеального перемешивания, в соответствии с ранее полученным уравнением имеет вид:

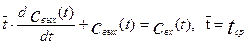
Преобразуем это уравнение по Лапласу:

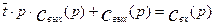(3.1.24)

Из уравнения (3.1.24) найдем передаточную функцию:

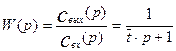(3.1.25)

Учитывая выражение (3.22), найдем выражение для F-кривой:

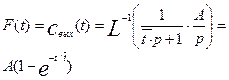(3.1.26)

Уравнение (3.1.26) полностью соответствует уравнению (3.1.10) полученному прямым интегрированием уравнения математической модели при ступенчатой функции изменения входной концентрации. График изменения этой функции во времени приведен на рис.3.1.2.

Аналогично найдем импульсную характеристику объекта полного перемешивания:

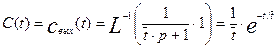(3.1.27)

При t=0, при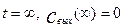

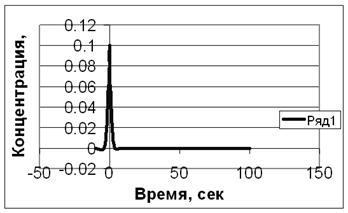
График изменения С – кривой показан на рис.3.1.3.

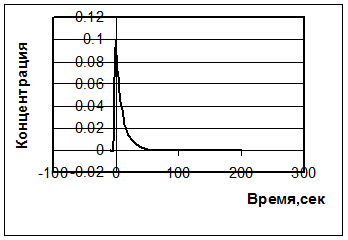Рис.3.1.3а. Зависимость входной концентрации от времени

Рис3.1.3.б. Зависимость выходной концентрации от времени.

Раздел 3.2.Модель идеального вытеснения.

Рассмотрим теперь модель аппарата полного, или идеального вытеснения.

В отличие от предыдущей модели, основным постулатом этой модели является допущение о том, что в направлении потока жидкость не перемешивается, в то время как в поперечном направлении жидкость перемешана полностью. При таких допущениях жидкость в аппарате движется подобно поршню, при этом каждый последующий слой вытесняется предыдущим. Поэтому эту модель называют еще моделью поршневого потока. В англоязычной литературе эта модель называется plug flow model. Схема аппарата представлена на рис.3.2.1.

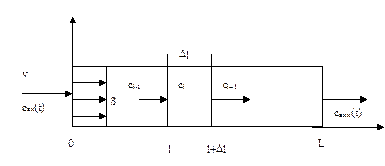
Рис.3.2.1 Схема аппарата идеального вытеснения.

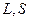– длина и площадь поперечного сечения аппарата,

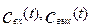- концентрация на входе и выходе из аппарата,

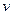- объемный расход смеси на входе и выходе из аппарата.

Выделим в аппарате элементарный объем 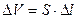и составим для него уравнение материального баланса, обозначив концентрацию в элементарном объеме через с_j, концентрацию на входе в слой через с_j-1, а концентрацию на выходе из объема через с_j+1. Накопление массы в рассматриваемом объеме будет равно интегралу от разности потоков, входящих и выходящих из рассматриваемого объема:

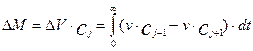(3.2.1)

Продифференцируем обе части уравнения (3.2.1) по времени и разделим на величину рассматриваемого объема 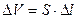. И рассмотрев предел уравнения при Dl®0, получим уравнение модели идеального вытеснения в следующем виде:

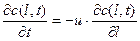(3.2.2)

Где 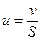- линейная скорость, м/с.

Эта модель представляет собой дифференциальное уравнение в частных производных, потому что переменная величина 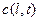изменяется в пространстве и времени. В уравнение (3.2.2) введем безразмерную пространственную координату x следующим образом:

Полученное значение производной поставим в уравнение (3.2.2) и получим математическую модель в следующем виде:

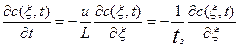(3.2.3)

Где 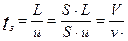- время пребывания смеси в аппарате.

Определим передаточную функцию аппарат идеального вытеснения. Для этого преобразуем уравнение (3.2.3) по Лапласу, считая x и t независимыми переменными, получим передаточную функцию модели аппарата идеального вытеснения в следующем виде:

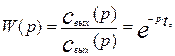(3.2.4)

Найдем реакцию модели на импульсное возмущение, т.е.

С – кривую, используя соотношение (3.1.23):

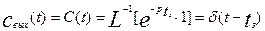(3.2.5)

Из этой формулы видно, что выходной сигнал будет повторять входной, но сдвинут на величину t_з. Аналогично можно найти выражение для F – кривой:

(3.2.6.

На рисунках 3.2.2 и 3.2.3. показаны графики С - кривой и F – кривой:

Рис.3.2.2. Кривые отклика аппарата идеального вытеснения на импульсное возмущение, а) – изменение входной концентрации, б) изменение выходной концентрации, t_з – время пребывания смеси в аппарате

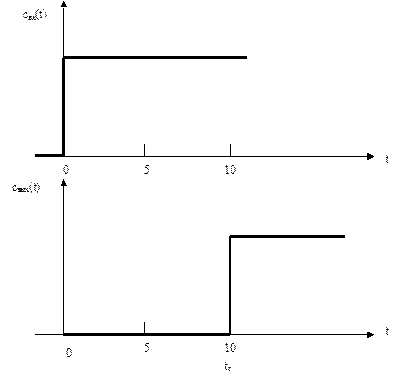
Рис.3.2.6. Кривые отклика аппарата идеального вытеснения на ступенчатое возмущение, а) – изменение входной концентрации, б) изменение выходной концентрации, t_з – время пребывания смеси в аппарате

Модель аппарата идеального вытеснения может быть использована для описания работы аппаратов, работающих по принципу вытеснения – колонные и трубчатые аппараты, теплообменники. Применение модели к описанию потоков в технологических аппаратах связывают с величиной отношения длины аппарата к его диаметру. При L/d >20 (d- диаметр аппарата) и числе Рейнольдса

Re>2300 продольное перемешивание незначительно, а турбулентное движение обеспечивает равномерно распределение концентрации по поперечному сечению аппарата. Таким образом, в этих условиях выполняются основные допущения, лежащие в основе модели идеального вытеснения.

3.3. Ячеечная модель аппарата

Ячеечную модель применяют для описания структуры потоков в аппаратах, потоки в которых не могут быть описаны моделями полного смешения или полного вытеснения. В этом случае предполагают, что весь объем аппарат может быть разделен на элементарные объемы, каждый из которых описывается моделью полного смешения. Такая модель применима также для описания потоков в каскаде последовательно соединенных аппаратов смешения. Рассмотрим движение смеси в таком каскаде аппаратов.

Рис.3.3.1 Схема ячеечной модели аппарата

v- объемный расход вещества, V_i объем ячейки (i=1,…,n) n – число ячеек,

c_i – концентрация вещества в i- м аппарате.

Составим математическое описание, описывающее структуру потоков в ячеечной модели.

Учитывая, что каждая ячейка представляет собой аппарат идеального смешения, для первой ячейки можно записать:

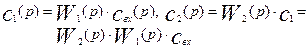
Продолжая эту операцию последовательно до последнего аппарата каскада, получим для выходной концентрации из каскада следующее выражение:

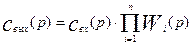(3.3.1)

Отсюда получаем выражение для передаточной функции ячеечной модели:

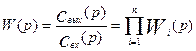(3.3.2)

Передаточная функция n последовательно соединенных ячеек полного смешения равна произведению передаточных функций отдельных ячеек.

При условии, что V₁= V₂= V_i= V_n и v=const передаточные функции отдельных ячеек будут равны и передаточная функция, будет иметь вид:

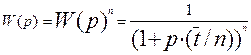(3.3.3)

Где 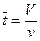- среднее время пребывания смеси во всем аппарате, 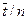- среднее время пребывания в одной ячейке.

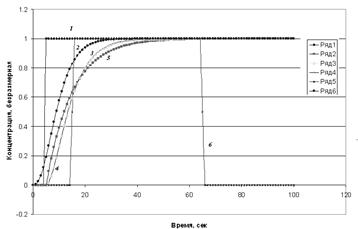Рис.3.3.2. Кривые отклика ячеечной модели при различном числе

ячеек на ступенчатое возмущение

Раздел 3.4. Диффузионная модель

Поршневой режим движения жидкостей, рассмотренный нами при выводе уравнения модели идеального вытеснения, в реальных процессах реализуется не всегда. На самом деле в реальных процессах жидкость в различных направлениях перемещается за счет следующих явлений:

· Турбулентности потока

· Конвективного переноса.

· Поперечной неравномерности профиля скорости.

· Пристеночных эффектов, каналообразования.

· Переноса за счет молекулярной диффузии.

Будем считать, что все отклонения режима движения от поршневого режима, могут быть сведены к переносу в обратном направлении, за счет влияния конвективной диффузии, или осевой дисперсии.

На рис 3.4.1. приведена схема потоков в таком аппарате:

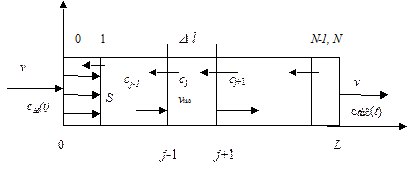Рис.3.4.1. Схема потоков в аппарате, описываемом диффузионной моделью.

V=S×L – объем аппарата, S=p×d²/4 – площадь поперечного сечения, L – длина аппарата.

Стрелками в обратном направлении обозначен перенос вещества в обратном направлении за счет конвективной диффузии или продольной дисперсии.

Составим уравнение материального баланса для аппарата с приведенной структурой потоков.

Поток вещества за счет турбулентной диффузии описывается уравнением, подобным уравнению диффузии Фика:

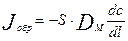(3.4.1)

Где J _обр- поток вещества в обратном направлении.

D _M – коэффициент обратного переноса массы за счет турбулентной диффузии.

Составим уравнение материального баланса для элементарного объема аппарата, ограниченного сечениями j-1 и j+1, расположенными на расстоянии Dl.

Приход вещества в рассматриваемый объем складывается из прихода за счет конвективного переноса и за счет обратного потока из предшествующего объема аппарата:

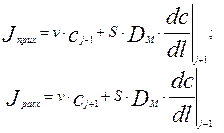(3.4.2)

Накопление массы в рассматриваемом элементарном объеме будет равно интегралу от разности входящего и выходящего потоков в объем:

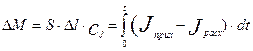(3.4.3)

Перейдем теперь от накопления массы в объеме к изменению концентрации. Для этого разделим обе части уравнения на величину элементарного объема DV=S×Dl и продифференцируем обе части уравнения по времени. С учетом того, что производная от интеграла по аргументу равна подинтегральному выражению и уравнения (3.4.2) для потоков прихода и расхода вещества, уравнение принимает следующий вид:

(3.4.4)

Рассмотрим пределы слагаемых правой части уравнения (3.4.4) при Dl®0.

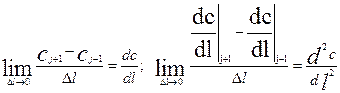(3.4.5)

Подставив выражения пределов из (3.4.5) в (3.4.4) получим окончательно уравнение диффузионной модели в следующем виде:

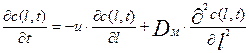(3.4.6)

Уравнение записано как дифференциальное уравнение в частных производных, так как концентрация является функцией двух независимых переменных с(l,t). В дальнейшем мы не будем это писать для сокращения записей но будем постоянно иметь в виду, что с=с(l,t).

Приведем уравнение к безразмерному виду с помощью следующих подстановок:

x=l/L, где l – текущая длина, а L – полная длина аппарата. Тогда Ldx=dl и dl²=L²dx². С использованием этих подстановок уравнение диффузионной модели может быть преобразовано к следующему виду:

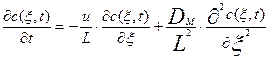(3.4.7)

Умножим обе части уравнения (3.4.7) на величину

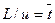- среднее время пребывания в аппарате. В итоге получим:

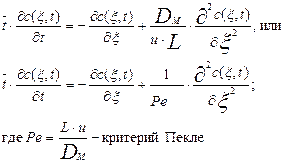(3.4.8)

Рассмотрим предельное выражение уравнения диффузионной модели при Ре® ¥. При Ре® ¥1 /Ре® 0. Таким образом, уравнение диффузионной модели превращается в следующее уравнение:

,

которое, является уравнением модели идеального вытеснения.

Для решения уравнения диффузионной модели преобразуем его по Лапласу по переменной t. В итоге получим:

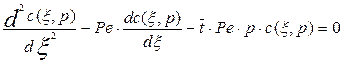(3.4.9)

Уравнение (3.4.9) представляет собой однородное обыкновенное дифференциальное уравнение с постоянными коэффициентами.

Его решение имеет вид:

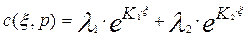((3.4.10)

Где K₁ и K₂ корни характеристического уравнения, соответствующего дифференциальному уравнению (3.4.9).

. Характеристическое уравнение для уравнения (3.4.9) будет иметь вид:

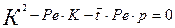(3.4.11

Найдем корни этого характеристического уравнения:

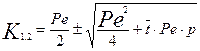(3.4.12

Обозначим первое слагаемое в уравнении (3.4.12 через a, а второе через b.

Корни характеристического уравнения можно записать в следующем виде:

, .

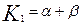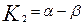Тогда общее решение уравнения (3.4.9) для случая когда 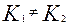(корни различные и действительные) можно записать в виде:

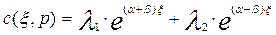(3.4.13

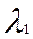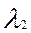где - и – постоянные интегрирования, определяемые из граничных условий.

Если (корни равные и действительные)

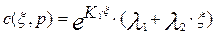(3.4.14

Если корни комплексные 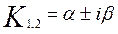- a- действительная часть, i×b -мнимая часть, то решение имеет вид:

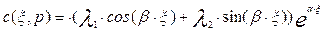(3.4.15

Постоянные интегрирования можно определить из граничных условий, выражающих закон сохранения массы на входе и выходе из аппарата, указанной на схеме рис.3.4.1. Приход массы в эту ячейку складывается из прихода с входным потоком и прихода за счет обратного диффузионного потока. Расход складывается из конвективного уноса массы в последующие объемы аппарата. Из равнения материального баланса на входе в аппарат следует:

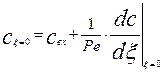(3.4.15

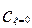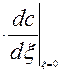Где и - концентрация и ее производная по безразмерной длине на воде в аппарат,

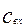- концентрация трассера во входном потоке.

И уравнения (3.4.15) следует, что концентрация вещества во входном сечении аппарата не равна концентрации во входном потоке, Она изменяется скачкообразно за счет действия обратного перемешивания.

Из уравнения материального баланса в выходном сечении аппарата определяем 2-е граничное условие:

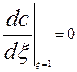(3.4.16).

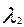Используя граничные условия (3.4.15) и (3.4.16) можно определить постоянные интегрирования и в уравнении (3.4.13). Для этого нужно определить значение концентрации и ее производной по длине во входном сечении при, 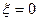, а также значение производной при . Подставив эти значения в уравнения (3.4.15) и (3.4.16), определим значения постоянных интегрирования

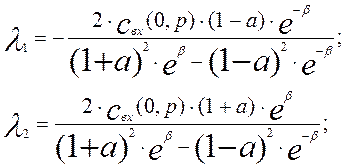(3.4.17)

где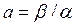

Подставив найденные выражения для постоянных интегрирования в уравнение (3.4.13), найдем уравнение для зависимости концентрации от длины и переменной Лапласа в следующем виде:

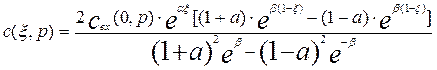(3.4.18)

найдем передаточную функцию аппарата с конечными размерами. Для этого вычислим значение выходной концентрации, положив в уравнении (3.4.19) x=1.

В итоге получим:

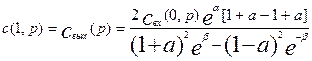(3.4.19)

откуда найдем передаточную функцию:

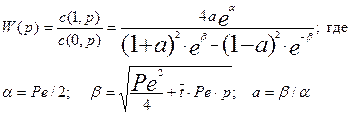(3.4.20)

Критерий Пекле 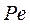и коэффициент продольной диффузии 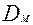, являющиеся параметрами диффузионной модели определяют экспериментально с использованием экспериментов с трассерами. Методы определения параметров модели по экспериментальным данным мы рассмотрим ниже.

Рассмотрим решение уравнения диффузионной модели для аппарата бесконечно больших размеров. В таком аппарате возмущения не доходят до его границ. Поэтому можно считать, что концентрация на входе в аппарат равна концентрации во входном потоке, а концентрация на выходе равна нулю, при 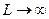. Для этого случая граничные условия будут иметь вид:

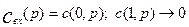, так как 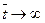. Для этих значений граничных условий решение уравнения диффузионной модели будет иметь следующий вид:

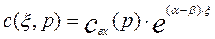(3.4.21)

Концентрация на выходе из аппарата будет равна:

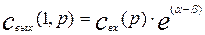(3.4.22)

Откуда передаточная функция аппарата бесконечно больших размеров будет равна:

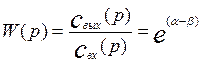(3.4.23)

Стационарный метод определения критерия Пекле .

Суть этого метода заключается в следующем. На некотором расстоянии от начала аппарата 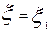вводится трассер с постоянной скоростью.

Когда процесс станет установившимся, т.е. ,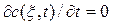

будет наблюдаться некоторое стационарное распределение концентрации трассера. Это распределение будет описываться стационарным уравнением диффузионной модели, которое получается из уравнения (4.3.8):

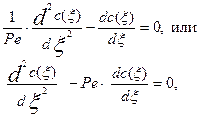(3.4.24

Решением уравнения (3.4.24) будет уравнение вида:

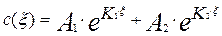(3.4.26)

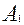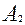где и постоянные интегрирования, которые находятся из граничных условий, соответствующих условиям проведения эксперимента, а 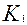и 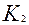корни характеристического уравнения соответствующего исходному дифференциальному уравнению (3.4.25). Характеристическое уравнение будет иметь вид:

.

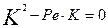Корни могут быть определены следующим образом:

.

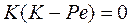Тогда

.

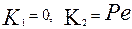С учетом этого уравнение (3.4.26) примет вид:

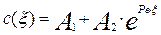(3.4.27)

Для нахождения 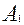воспользуемся первым граничным условием:

,

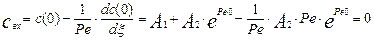Откуда следует, что 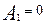, так как концентрация трассера на входе в аппарат равна нулю. Для нахождения 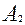воспользуемся вторым граничным условием, а именно: при

,

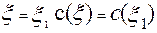следовательно,

,

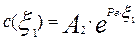или

.

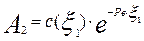Подставляя найденные значения постоянных интегрирования в (3.4.27), получим уравнение для описания стационарного профиля концентрации трассера:

(3.4.28)

Логарифмируя выражение (3.4.28), получим следующее уравнение:

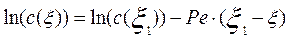(3.4.29)

Это уравнение представляет собой уравнение прямой в координатах

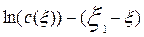
Найдя из графика тангенс угла наклона прямой линии a, можно рассчитать критерий Пекле по формуле

,

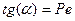зная критерий Пекле, можно рассчитать коэффициент обратной диффузии по формуле:

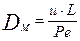(3.4.30)

Таким образом, для определения критерия Ре, необходимо определить ряд концентраций трассера по длине аппарата, отложить их в координатах

,

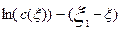и из полученной прямой определить критерий Пекле из тангенса угла наклона полученной прямой. Одновременно определяется адекватность применения диффузионной модели для описания движения потока в данном аппарате.

Рис.3.11. Определение числа Пекле методом стационарного ввода трассера.

3.5.Комбинированные модели

Не все реальные процессы могут быть описаны с помощью рассмотренных моделей. К таким процессам относятся процессы, включающим байпасные и циркуляционные потоки, а также застойные зоны. При построении комбинированных моделей принимают, что аппарат состоит из отдельных зон, соединенных между собой последовательно или параллельно, причем каждая из зон может быть описана одной из рассмотренных выше идеальных моделей. Следует отметить, что увеличением количества зон можно описать процесс любой сложности, однако полученное при этом математическое описание получается достаточно сложным для анализа. Рассмотрим несколько типов комбинированных моделей.

3.5.1.Модель с застойной зоной

Застойная зона – это участок в объеме аппарата, в котором происходит слабое перемешивание, и обмен этого участка с остальным объемом аппарат затруднен. В соответствии с этим допущением весь объем аппарата может быть разделен на две части – хорошо перемешиваемый объем V_o и объем застойной зоны V_зз.

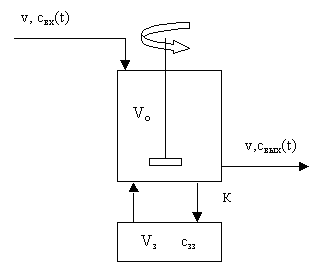Рис.3.5.1 Схема аппарата с застойной зоной.

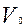– объем части аппарата идеального смешения,

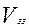– объем застойной зоны, 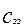– концентрация в застойной зоне

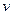- объемный расход смеси через аппарат, 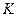– коэффициент обмена между застойной и перемешиваемой частями аппарата, 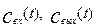- концентрация на входе и выходе из аппарата

Для получения математической модели составим обобщенное уравнение материального баланса для каждой зоны.

· Для хорошо перемешиваемой зоны:

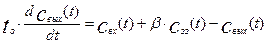(3.5.1)

где 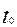– время пребывания в хорошо перемешиваемой зоне, 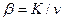- коэффициент, учитывающий интенсивность обмена проточной части с застойной зоной.

· Для застойной зоны

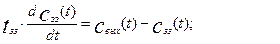(3.5.2)

где 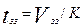– среднее время пребывания вещества в объеме застойной зоны..

Преобразуем уравнения (3.5.1) и (3.5.2) по Лапласу:

;

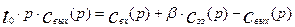(3.5.3)

;

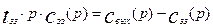Из второго уравнения системы (3.5.3) найдем :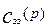

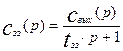
и подставим его в первое уравнение системы:

(3.5.4)

Из уравнения (3.5.4) найдем передаточную функцию модели с застойной зоной в следующем виде

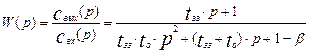(3.5.5)

Полученная передаточная функция соответствует модели идеального смешения с застойной зоной. На рис.3.5.2 показаны кривые разгона модели идеального перемешивания и модели с застойной зоной при равных общих объемах аппаратов. Для аппарата с застойной зоной характерно более быстрое изменение в начальные моменты времени и более медленное изменение в конце процесса. Появляется затянутый «хвост» кривой, соответствующий медленному вымыванию трассера из застойной зоны.

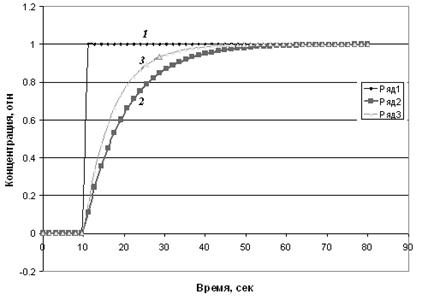
Рис.3.5.2. Кривые разгона аппарата идеального перемешивания (Ряд-2) и аппарата с застойной зоной (Ряд 3) при ступенчатом возмущении на входе (Ряд 1)

3.5.2.Модель с байпасным потоком.

Модель с байпасным потоком описывает ситуацию, когда часть входного потока проскакивает на выход не смешиваясь с содержимым аппарата.

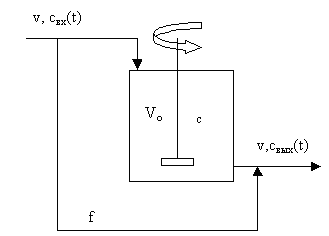На рис. 3.5.3. приведена схема аппарата с байпасированием части потока.

Рис.3.5.3. Схема аппарата с байпасированием части потока.

Здесь V_o – объем аппарата с интенсивным смешением, c- концентрация в объеме зоны смешения, f- доля байпасного потока.

Концентрация в аппарате описывается дифференциальным уравнением:

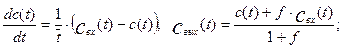(3.5.6)

Откуда передаточная функция аппарат с байпасированием потока будет иметь вид:

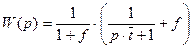(3.5.7)

Где 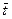среднее время пребывания реакционной смеси в проточной части аппарата.

f - доля байпасной части потока

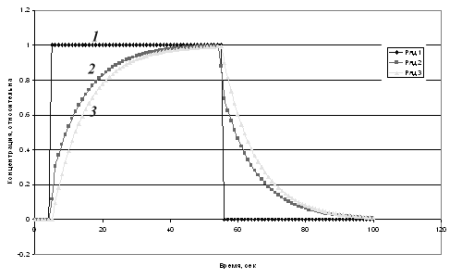
Рис.3.5.4.Кривые отклика аппарата идеального перемешивания и аппарата с байпасным потоком на ступенчатое импульсное возмущение.

1- входной ступенчатый импульс

2- выходная кривая для аппарата с байпасным потоком

3- выходная кривая для аппарата идеального перемешивания

3.5.3. Последовательное соединение ячеек идеального вытеснения и идеального смешения.

На рис.3.5.4 представлена схема аппарата в виде последовательного соединения зон идеального вытеснения и зон идеального смешения.

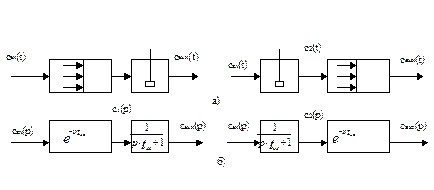Рис. 3.5.4. Схема комбинированной модели аппарата с последовательным соединением зоны идеального вытеснения и зоны идеального смешения при различной последовательности их расположения.

а) схема расположения аппаратов; б)- структурная схемы.

Из рисунка видно, что передаточная функция последовательно включенных звеньев равна произведению передаточных функций отдельных звеньев. Таким образом, общая передаточная функция комбинированной модели будет иметь следующий вид:

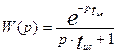(3.5.8)

Математически передаточная функция будет одинакова, независимо от последовательности включения звеньев. При этом кривые отклика будут иметь одинаковый вид при замере выходной концентрации на выходе из всех звеньев. Для различия порядка включения звеньев нужно замерять концентрации в промежуточных точках соединения звеньев. На рис. 3.5.5 показаны кривые разгона этой модели, при различной последовательности их расположения. Следовательно, одинаковые кривые отклика аппаратов на ступенчатый сигнал (или другого типа воздействие) – это еще не полная информация о гидродинамике потока.

а)

б)

Рис.3.5.5. Кривые отклика комбинированной модели идеального перемешивания (ИП) и идеального вытеснения (ИВ) при раличной последовательности их соединения

3.5.4.Гидродинамические модели многофазных

потоков.

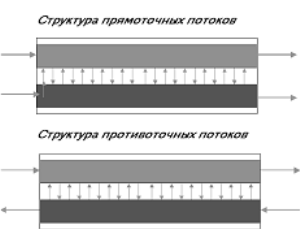Для описания процессов в технологических аппаратах, через которые протекают многофазные потоки реагирующих компонентов применяют обычно разработанные гидродинамические модели однофазных потоков для каждой из фаз. Эти модели дополняются источниковыми членами, учитывающими массо- и теплообмен между фазами, а также источниковыми членами, учитывающими превращение веществ за счет химических реакций и тепловыделение (или теплопоглощение) за счет химических превращений и фазовых переходов. Используемая структура потоков в многофазных реакторах и технологических объектах показана на рисунке:

Рис.3.5.3.Структура многофазных потоков

Используем диффузионную гидродинамическую модель для описания процессов в аппаратах с многофазными потоками, так как ранее было показано, что диффузионная модель содержит в себе, в качестве предельных случаев и модель идеального вытеснения (при D ®0) и модель идеального перемешивания (при D ® ¥).

Ниже приведены уравнения, описывающие процессы переноса тепла и вещества в пределах каждой из фаз потоков, с учетом тепло - массообмена между фазами:

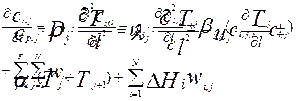где 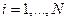– число реагирующих компонентов компонентов.

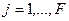– число фаз, образующих потоки регентов.

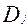- коэффициент диффузионного перемешивания в 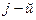фазе

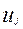-линейная скорость движения потока 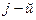фазы

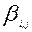- коэффициент массопередачи 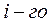в фазу

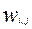– скорость реакции 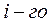компонента в 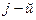фазе

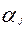– коэффициент теплопередачи между фазами

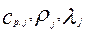– теплоемкость, плотность и теплопроводность 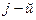фазы.

Аналогичные уравнения можно получить для многофазных систем и при использовании других моделей гидродинамики, при этом можно использовать различные модели для каждой из фаз.

3.6.Методы определения параметров моделей

структуры потоков.

Дата добавления: 2014-11-29